Avant-propos

Cet article est en grande partie une traduction de l’article de Jay Alammar : The illustrated transformer. Merci à lui de m’avoir autorisé à effectuer cette traduction. J’ai ajouté des éléments supplémentaires quand j’estimais que cela était pertinent.


Introduction

Dans l’article Le Seq2seq et le processus d’attention nous avons introduit l’attention, une méthode omniprésente dans les modèles modernes d’apprentissage profond. L’attention est un concept qui a permis d’améliorer les performances des applications de traduction automatique. Dans celui-ci, nous nous intéresserons au transformer, un modèle qui utilise l’attention pour augmenter la vitesse à laquelle ces modèles peuvent être entraînés. Le transformer surpasse le modèle de traduction automatique de Google dans des tâches spécifiques. Le plus grand avantage, vient de la façon dont le transformer se prête à la parallélisation. C’est en effet la recommandation de Google Cloud d’utiliser le Transformer comme modèle de référence pour utiliser leur offre Cloud TPU. Essayons donc de décomposer le modèle et de voir comment il fonctionne.

Le transformer a été proposé dans le document Attention is All You Need de A. Vaswani et al. (2017). Une implémentation en TensorFlow est disponible dans le cadre du package Tensor2Tensor. Le groupe NLP de Harvard a créé un guide avec l’implémentation en PyTorch. Dans cet article, nous tenterons de simplifier les choses et d’introduire les concepts un par un pour, espérons-le, faciliter la compréhension des lecteurs n’ayant pas une connaissance approfondie du sujet.


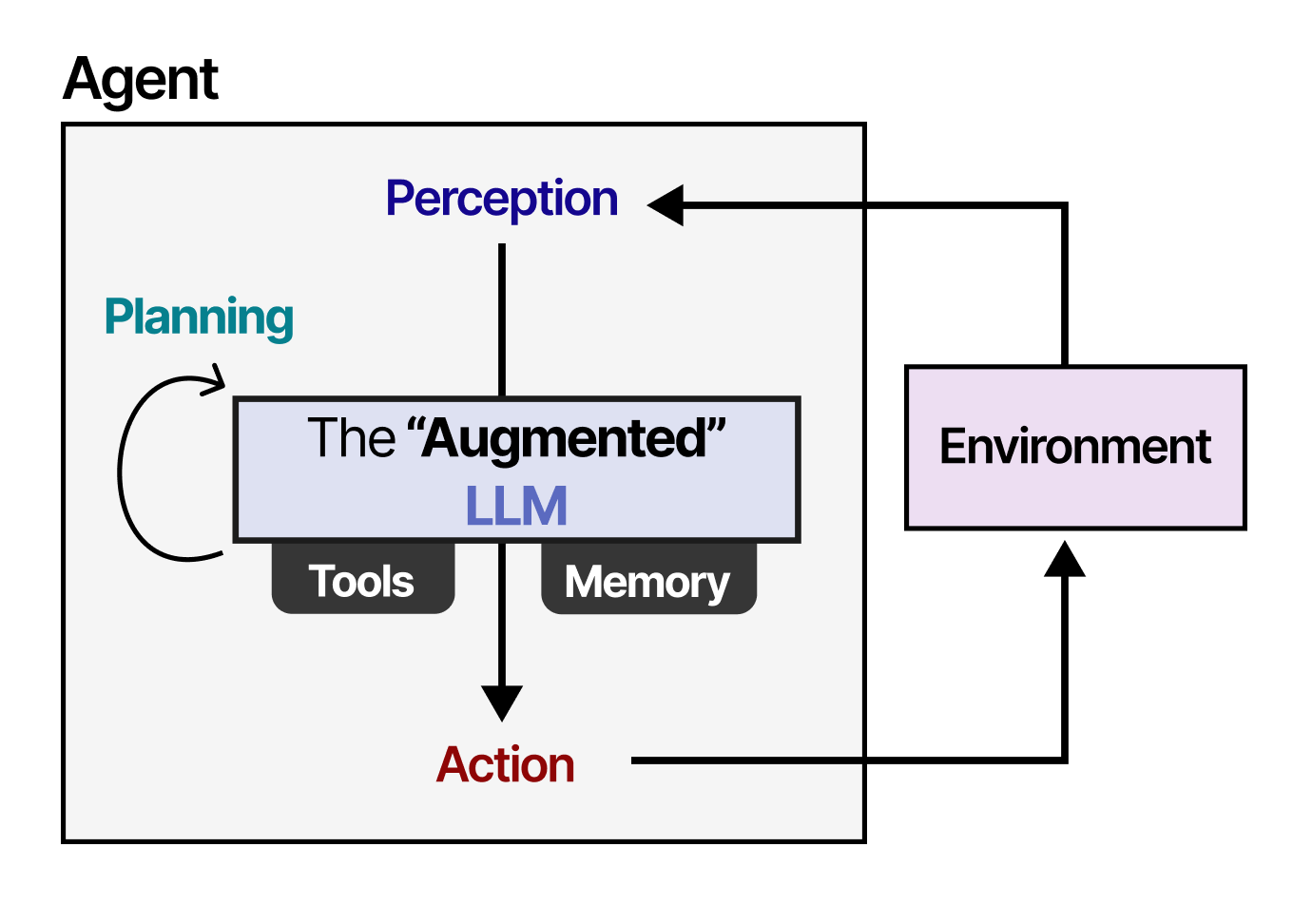
1. Un look de haut niveau

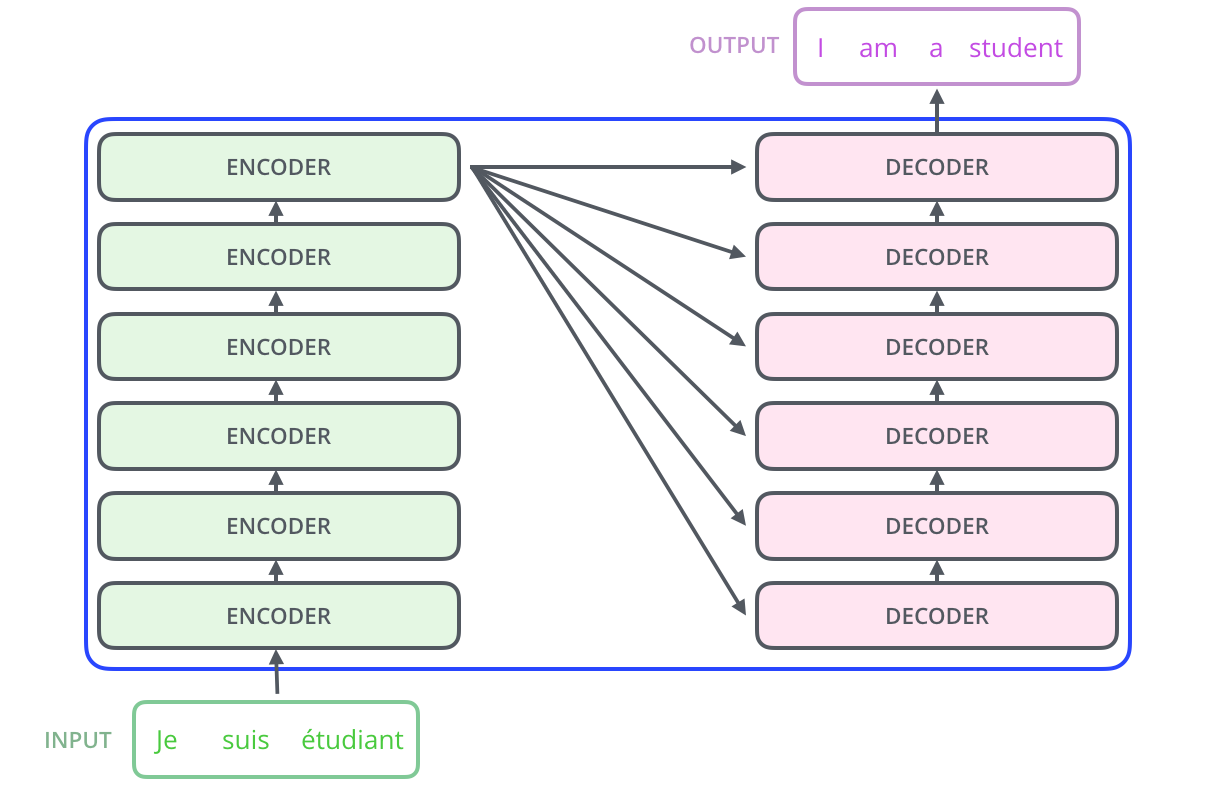
Commençons par considérer le modèle comme une boîte noire. Dans une application de traduction automatique, il prend une phrase dans une langue et la traduirait dans une autre.

En ouvrant la boite, nous voyons un composant d’encodage, un composant de décodage et des connexions entre eux.

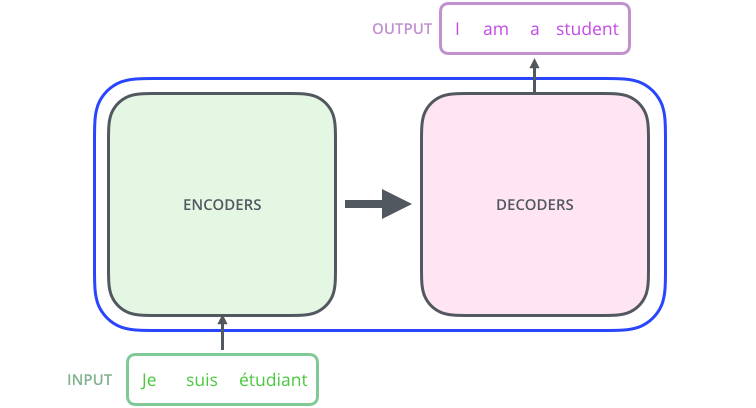
Le composant d’encodage est une pile d’encodeurs (l’article empile six encodeurs les uns sur les autres, ce nombre n’a rien de magique, on peut certainement expérimenter avec d’autres arrangements). Le composant de décodage est une pile de décodeurs du même nombre.

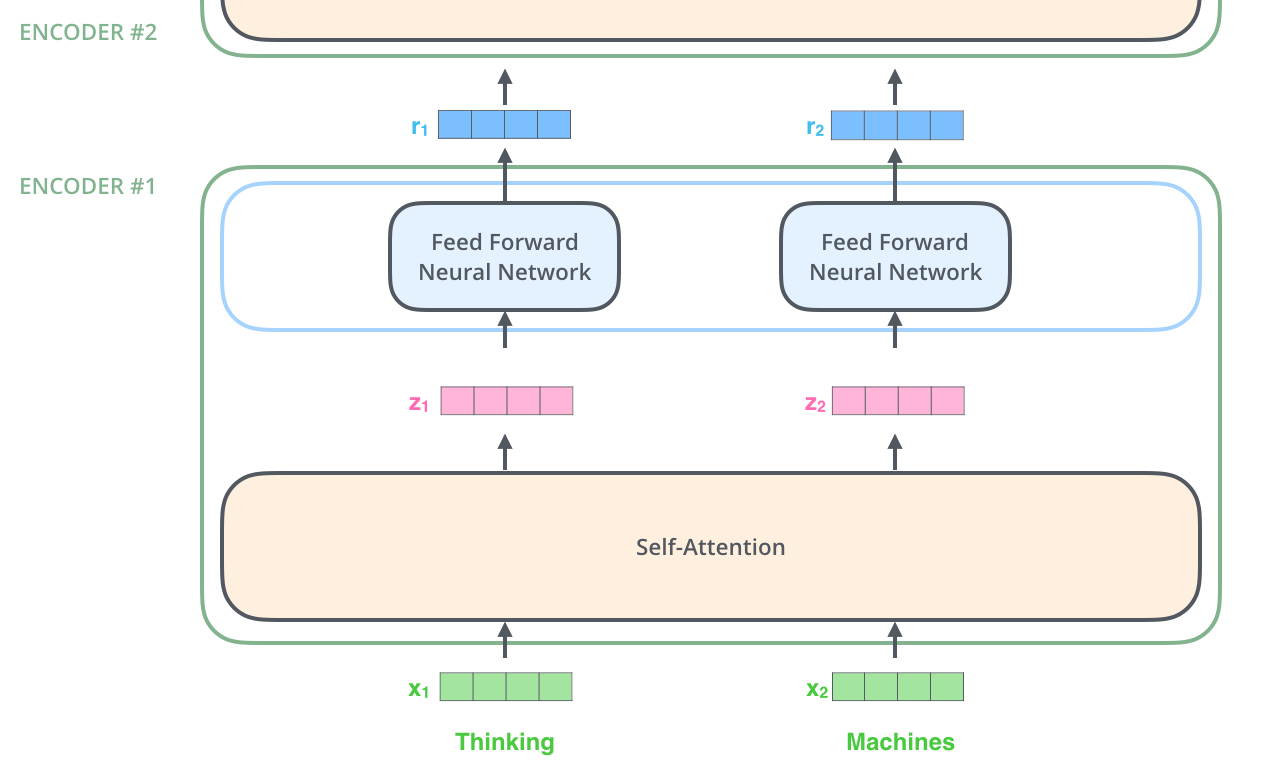
Les encodeurs sont tous identiques mais ils ne partagent pas leurs poids. Chacun est divisé en deux sous-couches :

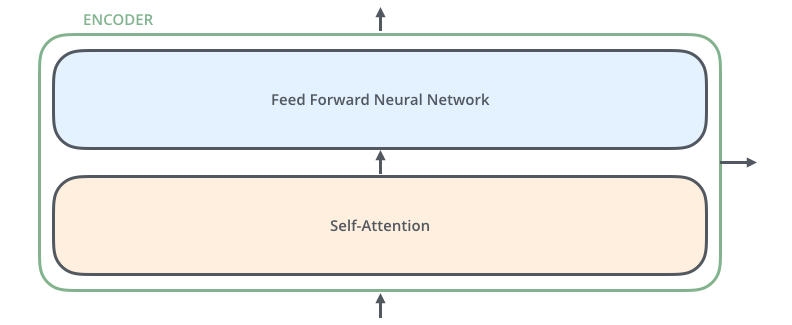
Les entrées de l’encodeur passent d’abord par une couche d’auto-attention : une couche qui aide l’encoder à regarder les autres mots dans la phrase d’entrée lorsqu’il code un mot spécifique. Nous examinerons plus end détails la question de l’auto-attention plus loin dans l’article.

Les sorties de la couche d’auto-attention sont transmises à un réseau feed-forward. Le même réseau feed-forward est appliqué indépendamment à chaque encodeur.

Le décodeur possède ces deux couches, mais entre elles se trouve une couche d’attention qui aide le décodeur à se concentrer sur les parties pertinentes de la phrase d’entrée (comme dans les modèles seq2seq).




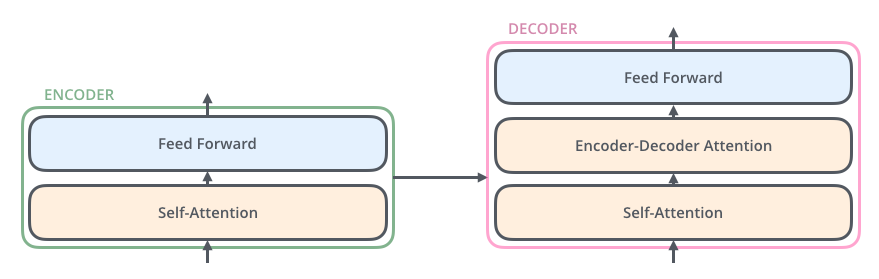
2. Les tenseurs

Maintenant que nous avons vu les principales composantes du modèle, commençons à examiner les différents vecteurs/tenseurs et la façon dont ils circulent entre ces composantes pour transformer l’entrée d’un modèle entrainé en sortie.

Comme c’est le cas dans les applications de traitement du langage naturel en général, nous commençons par transformer chaque mot d’entrée en vecteur à l’aide d’un algorithme d’enchâssement.

Chaque mot est mis dans un vecteur de taille 512. Nous représentons ces vecteurs avec ces simples boîtes.

L’enchâssement n’a lieu que dans l’encodeur inférieur. Le point commun à tous les encodeurs est qu’ils reçoivent une liste de vecteurs de la taille 512. Dans l’encodeur du bas il s’agit de l’enchâssement des mors mais dans les autres encodeurs, c’est la sortie de l’encodeur qui est juste en dessous.

La taille de la liste est un hyperparamètre que nous pouvons définir. Il s’agit essentiellement de la longueur de la phrase la plus longue dans notre ensemble de données d’entraînement.

Après avoir enchassé les mots dans notre séquence d’entrée, chacun d’entre eux traverse chacune des deux couches de l’encodeur.

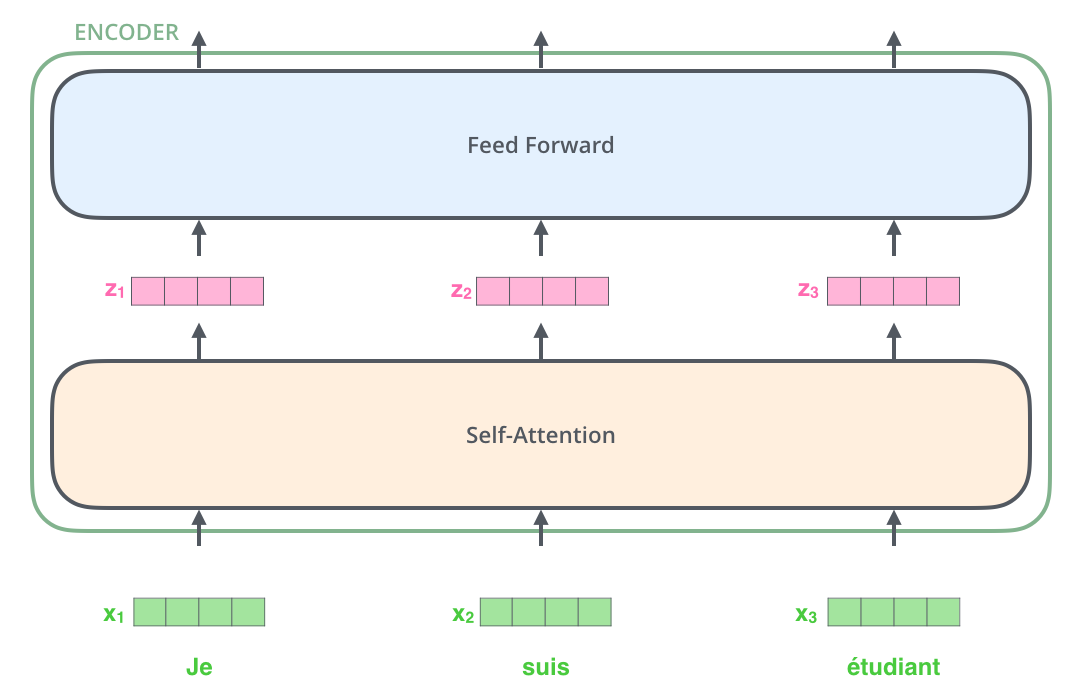
Nous commençons à voir une propriété clé du transformer : dans chacune des positions, le mot circule à travers son propre chemin dans l’encodeur. Il y a des dépendances entre ces chemins dans la couche d’auto-attention.

La couche feed-forward n’a pas ces dépendances et donc les différents chemins peuvent être exécutés en parallèle lors de cette couche.

Ensuite, nous allons commuter l’exemple sur une phrase plus courte et regarder ce qui se passe dans chaque sous-couche de l’encodeur.


3. L’encodage

Comme nous l’avons déjà mentionné, un encodeur reçoit une liste de vecteurs en entrée. Il traite cette liste en passant ces vecteurs dans une couche d’auto-attention, puis dans un réseau feed-forward, et enfin envoie la sortie vers le haut au codeur suivant.

Le mot à chaque position passe par un processus d’auto-attention. Ensuite, chacun d’eux passe par un réseau feed-forward (le même réseau feed-forward pour chaque vecteur mais chacun le traverse séparément).




4. Introduction à l’auto-attention

Ne vous laissez pas berner par le mot « d’auto-attention » que je lance comme si c’était un concept que tout le monde devrait connaître. Regardons son fonctionnement.

Disons que la phrase suivante est une phrase d’entrée que nous voulons traduire : « The animal didn’t cross the street because it was too tired ».

A quoi se réfère « it » dans cette phrase ? Est-ce qu’il fait référence à la rue ou à l’animal ? C’est une question simple pour un humain, mais pas pour un algorithme.

Lorsque le modèle traite le mot « it », l’auto-attention lui permet d’associer « it » à « animal ».

Au fur et à mesure que le modèle traite chaque mot (chaque position dans la séquence d’entrée, l’auto-attention lui permet d’examiner d’autres positions dans la séquence d’entrée à la recherche d’indices qui peuvent aider à un meilleur codage pour ce mot.

L’auto-attention est la méthode que le transformer utilise pour améliorer la compréhension du mot qu’il est en train de traiter en fonction des autres mots pertinents.

Comme nous codons le mot « it » dans l’encodeur#5, une partie du mécanisme d’attention se concentre sur « The Animal ».

Vous pouvez jouer avec la visualisation interactive en consultant le notebook Tensor2Tensor.


5. L’auto-attention en détail

Voyons d’abord comment calculer l’auto-attention à l’aide de vecteurs, puis comment elle est réellement mise en œuvre à l’aide de matrices.

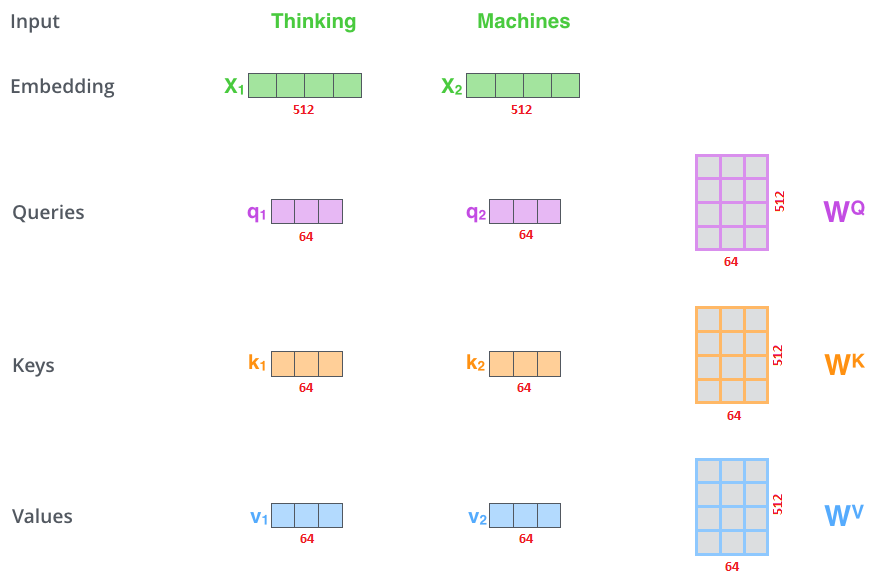
La première étape du calcul de l’auto-attention consiste à créer trois vecteurs à partir de chacun des vecteurs d’entrée \(x_{i}\) de l’encodeur (dans ce cas, l’enchâssement de chaque mot).

Chaque vecteur d’entrée \(x_{i}\) est utilisé de trois manières différentes dans l’opération d’auto-attention :

  • Il est comparé à tous les autres vecteurs pour établir les pondérations pour sa propre sortie \(y_{i}\). Cela forme le vecteur de requête (query en anglais et dans les figures suivantes).
  • Il est comparé à tous les autres vecteurs pour établir les pondérations pour la sortie du j-ème vecteur \(y_{j}\). Cela forme le vecteur de clé (key).
  • Il est utilisé comme partie de la somme pondérée pour calculer chaque vecteur de sortie une fois que les pondérations ont été établies. Cela forme le vecteur de valeur (value).

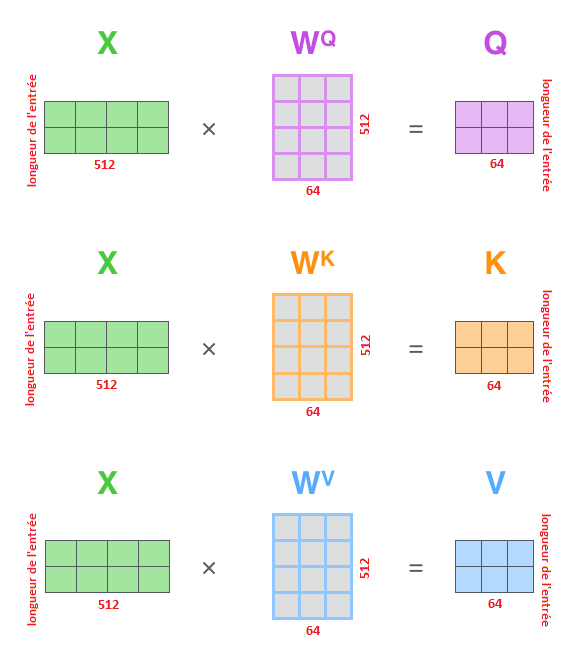
Ces vecteurs sont créés en multipliant l’enchâssement par trois matrices que nous avons entraînées pendant le processus d’entraînement. On a donc : \(q_{i}\) = \(W^{q}\) \(x_{i}\) , \(k_{i}\) = \(W^{k}\) \(x_{i}\) et \(v_{i}\) = \(W^{v}\) \(x_{i}\)

Notez que ces nouveaux vecteurs sont de plus petite dimension que le vecteur d’enchâssement (64 contre 512). Ils n’ont pas besoin d’être plus petits. C’est un choix d’architecture pour rendre la computation des têtes d’attentions constante.

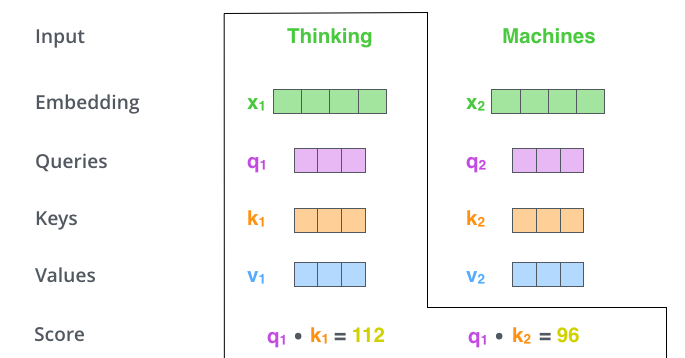
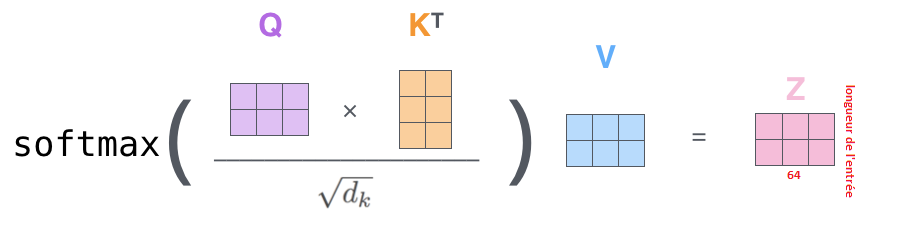
Les nombres indiqués en rouge correspondent aux dimensions de chaque vecteur/matrices

La deuxième étape du calcul de l’auto-attention consiste à calculer un score. Disons que nous calculons l’auto-attention pour le premier mot de cet exemple, « Thinking ». Nous devons noter chaque mot de la phrase d’entrée par rapport à ce mot. Le score détermine le degré de concentration à placer sur les autres parties de la phrase d’entrée au fur et à mesure que nous codons un mot à une certaine position.

Le score est calculé en prenant le produit scalaire du vecteur de requête avec le vecteur clé du mot que nous évaluons. Donc, si nous traitons l’auto-attention pour le mot en position #1, le premier score serait le produit scalaire de \(q_{1}\) et \(k_{1}\). Le deuxième score serait le produit scalaire de \(q_{1}\) et \(k_{2}\).

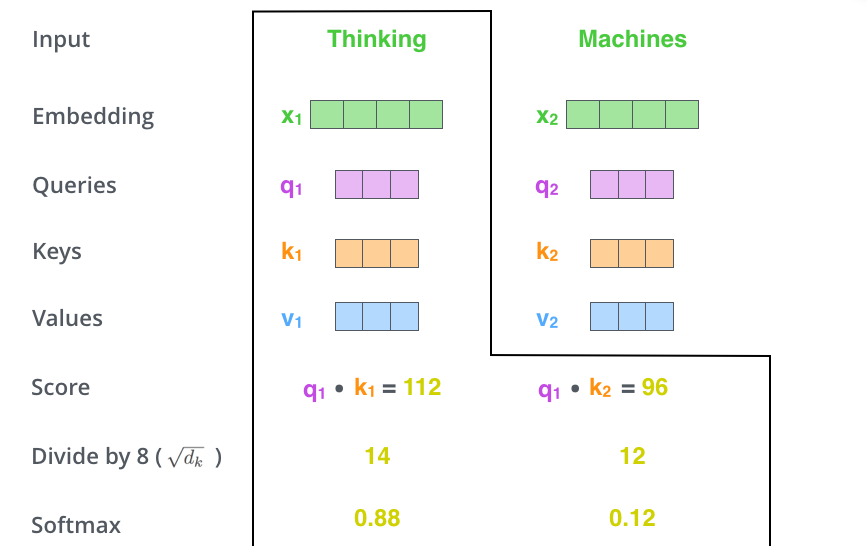
Les troisièmes et quatrièmes étapes consistent à diviser les scores par la racine carrée de la dimension des vecteurs clés utilisés (ici on divise donc par 8). Cela permet d’obtenir des gradients plus stables.

En effet, la fonction softmax que nous appliquons ensuite peut être sensible à de très grandes valeurs d’entrée. Cela tue le gradient et ralentit l’apprentissage, ou l’arrête complètement. Puisque la valeur moyenne du produit scalaire augmente avec la dimension de l’enchâssement, il est utile de redimensionner un peu le produit scalaire pour empêcher les entrées de la fonction softmax de devenir trop grandes.

Il pourrait y avoir d’autres valeurs possibles que la racine carrée de la dimension mais c’est la valeur par défaut.

L’application de la fonction softmax permet de normaliser les scores pour qu’ils soient tous positifs et somment à 1.

Ce score softmax détermine à quel point chaque mot est exprimé à sa position. Il est donc logique que le mot a le score de softmax le plus élevé à sa position et le score des autres mots permet de déterminer leur pertinence par rapport au mot traité.

La cinquième étape consiste à multiplier chaque vecteur de valeur par le score softmax (en vue de les additionner). L’intuition ici est de garder intactes les valeurs du ou des mots sur lesquels nous voulons nous concentrer et de noyer les mots non pertinents (en les multipliant par exemple par de petits nombres comme 0,001).

La sixième étape consiste à additionner les vecteurs de valeurs pondérées. Ceci produit la sortie de la couche d’auto-attention à cette position (ici pour le premier mot).



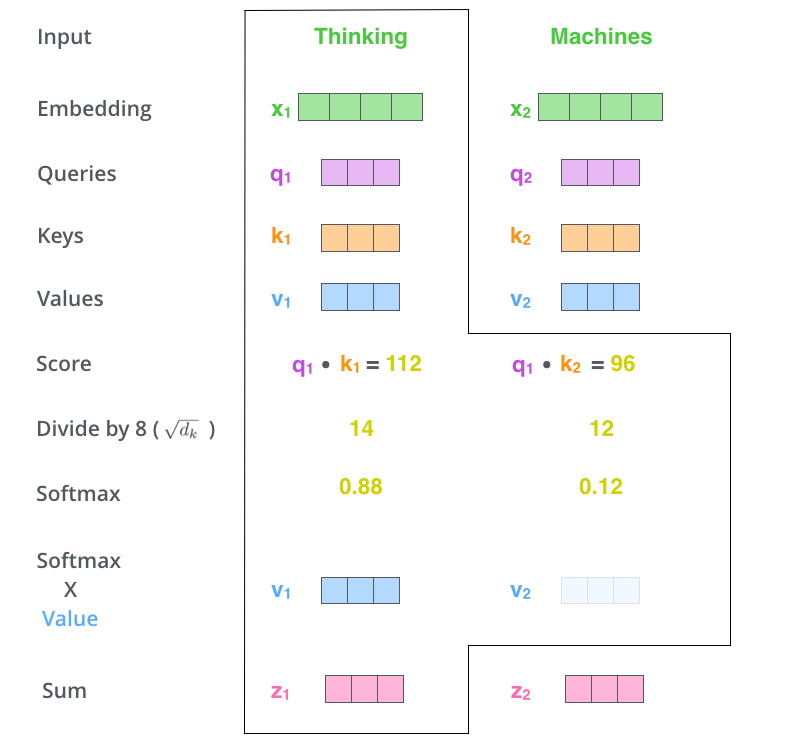
Résumons toutes ces étapes sous la forme d’un tableau et itérons le processus sur plusieurs mots :

Tableau pour le traitement du mot « Bonjour »
Tableau pour le traitement du mot « je »
Tableau pour le traitement du mot « suis »

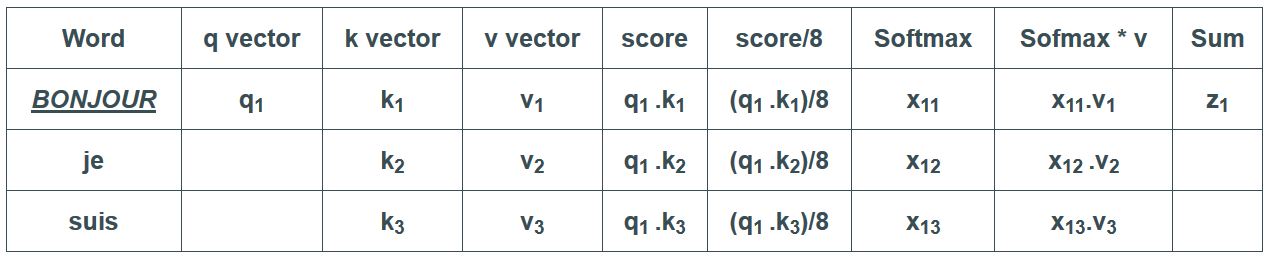
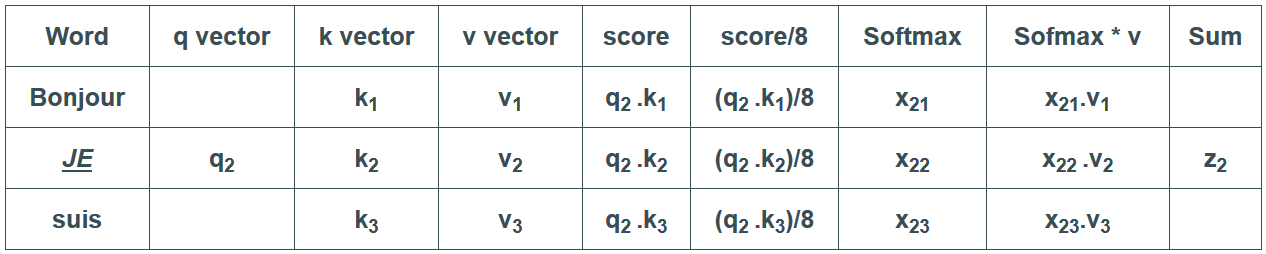
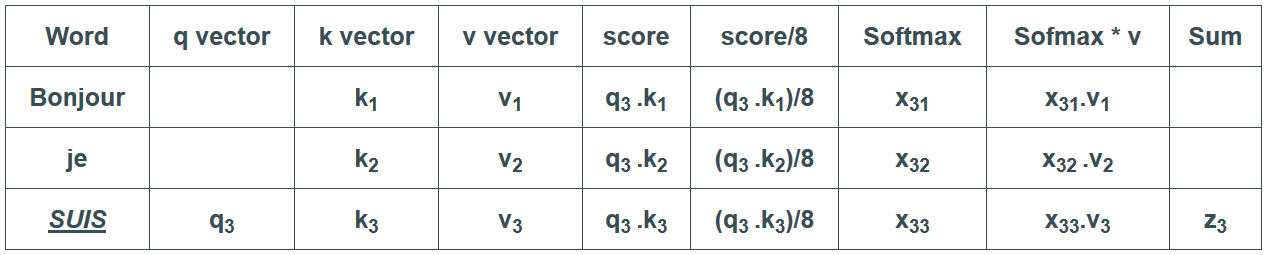
Voilà qui conclut le calcul de l’auto-attention. Les vecteurs zi résultants peuvent être envoyés au réseau feed-forward. En pratique cependant, ce calcul est effectué sous forme de matrice pour un traitement plus rapide. Maintenant que nous avons vu l’intuition du calcul au niveau d’un vecteur, regardons donc comment cela se déroule au niveau matriciel.


6. Les matrices de calcul de l’auto-attention

La première étape consiste à calculer les matrices Requête, Clé et Valeur. Pour ce faire, nous concaténons nos enchâssements dans une matrice X et nous la multiplions par les matrices de poids que nous avons entraînés (\(W^{Q}\), \(W^{K}\), \(W^{V}\)).

Chaque ligne de la matrice X correspond à un mot de la phrase d’entrée. Nous voyons à nouveau la différence de taille entre le vecteur d’enchâssement (512, ou 4 cases dans la figure), et les vecteurs q/k/v (64, ou 3 cases dans la figure).

Enfin, puisqu’il s’agit de matrices, nous pouvons condenser les étapes 2 à 6 en une seule formule pour calculer les sorties de la couche d’auto-attention.




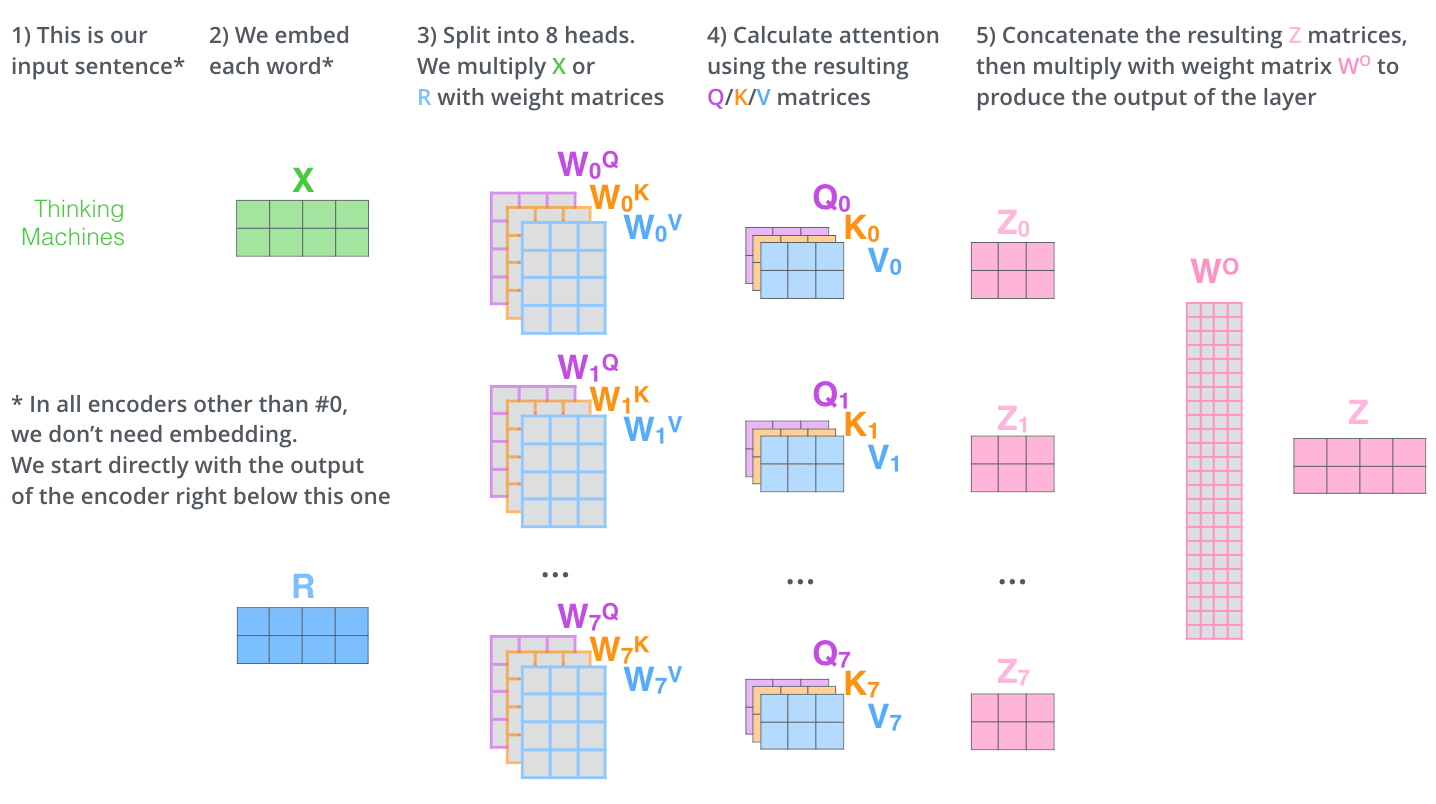
7. La bête à plusieurs têtes

Au lieu d’exécuter une seule fonction d’attention les auteurs de l’article ont trouvé avantageux de projeter linéairement les requêtes, les clés et les valeurs h fois avec différentes projections linéaires apprises sur les dimensions \(d_{k}\), \(d_{k}\) et \(d_{v}\), respectivement.

Ce mécanisme est appelé « attention multi-têtes ». Cela améliore les performances de la couche d’attention de deux façons :

  • Il élargit la capacité du modèle à se concentrer sur différentes positions. Prenons l’exemple suivant : « Marie a donné des roses à Susane » (exemple provenant du blog de Peter Bloem, en anglais). Nous voyons que le mot « donné » a des relations différentes aux différentes parties de la phrase. « Marie » exprime qui fait le don, « roses » exprime ce qui est donné, et « Susane » exprime qui est le destinataire. En une seule opération d’auto-attention, toutes ces informations ne font que s’additionner. Si c’était Suzanne qui avait donné les roses plutôt que Marie, le vecteur de sortie \(z_{donné}\) serait le même, même si le sens a changé.
  • Il donne à la couche d’attention de multiples « sous-espaces de représentation ». Comme nous le verrons plus loin, avec l’attention à plusieurs têtes, nous n’avons pas seulement un, mais plusieurs ensembles de matrices de poids Query/Key/Value (le transformer utilise huit têtes d’attention, donc nous obtenons huit ensembles pour chaque encodeur/décodeur). Chacun de ces ensembles est initialisé au hasard. Ensuite, après l’entraînement, chaque ensemble est utilisé pour projeter les enchâssements d’entrée (ou les vecteurs des encodeurs/décodeurs inférieurs) dans un sous-espace de représentation différent.
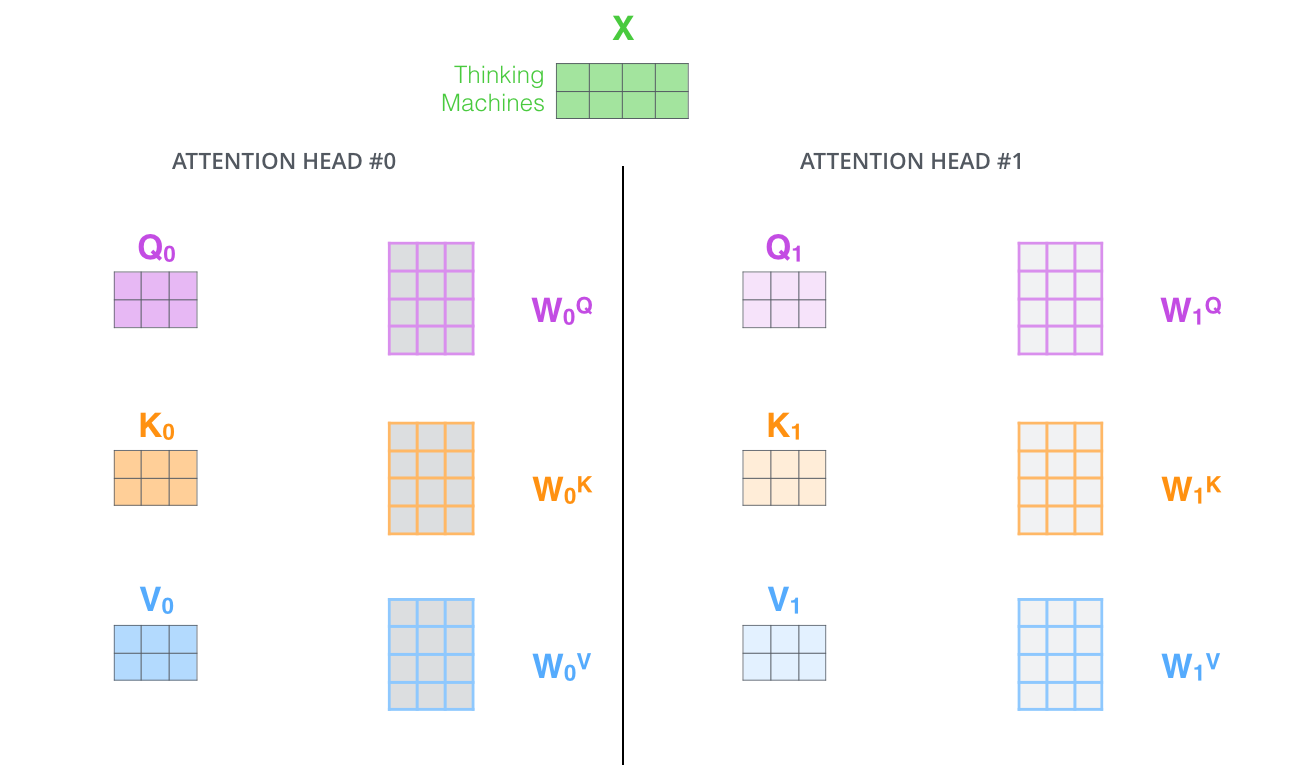
Avec plusieurs têtes d’attention, nous avons maintenons des matrices de poids Q/K/V distinctes pour chaque tête, ce qui donne des matrices Q/K/V différentes. Comme nous l’avons fait auparavant, nous multiplions X par les matrices WQ/WK/WV pour produire des matrices Q/K/V.

Si nous faisons le même calcul d’auto-attention que nous avons décrit ci-dessus, huit fois avec des matrices de poids différentes, nous obtenons huit matrices Z différentes.

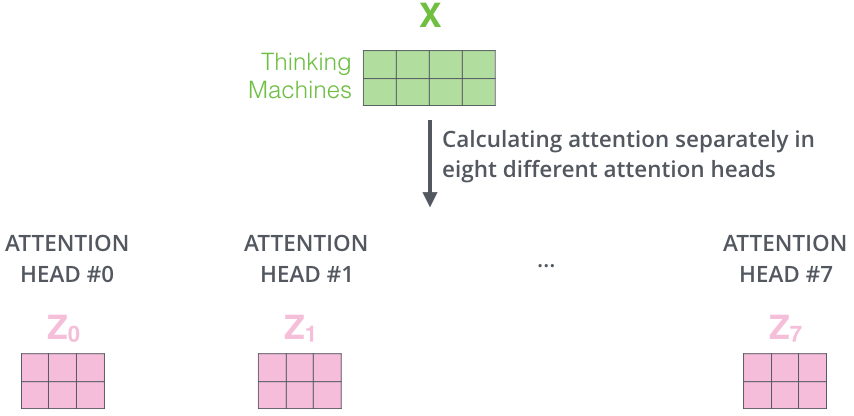
On obtient 8 matrices Zi de dimension 64 et 8×64 = 512

Il nous reste donc un petit défi à relever. La couche feed-forward n’attend pas huit matrices : elle n’attend qu’une seule (un vecteur pour chaque mot). Nous avons donc besoin d’un moyen de condenser ces huit éléments en une seule matrice.

Comment faire cela ? En concaténant les matrices puis les multipliant par une matrice de poids supplémentaire \(W_{O}\).

Résumons l’ensemble des étapes sous la forme d’un unique graphique récapitulatif :

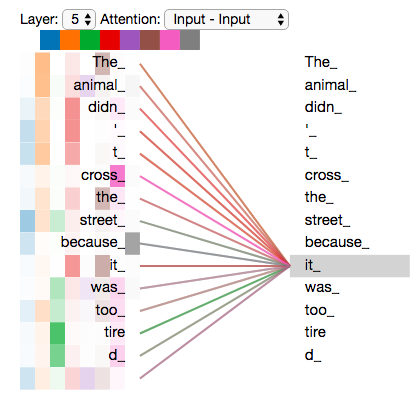
Maintenant que nous avons abordé les têtes d’attention, revoyons notre exemple pour voir où les différentes têtes d’attention se concentrent alors que nous codons le mot « it » dans notre phrase d’exemple :

Comme nous codons le mot « *it* », une tête d’attention (traits en orange) se concentre sur « *the animal* », tandis qu’une autre (traits en vert) se concentre sur « *tired* ».

Si nous ajoutons toutes les têtes d’attention sur l’image, les choses peuvent être plus difficiles à interpréter :



Un outil de visualisation dynamique des têtes d’attention très intéressant est proposé par Jesse Vig. Celui-ci est intitulé BertViz. Un article Medium présentant l’application de cet outil au modèle BERT est disponible ici (en anglais). Depuis la rédaction de cet article, l’outil a été élargi et prend maintenant en compte toutes les architectures de la librairie transformers d’Hugging Face. Une vidéo de présentation :




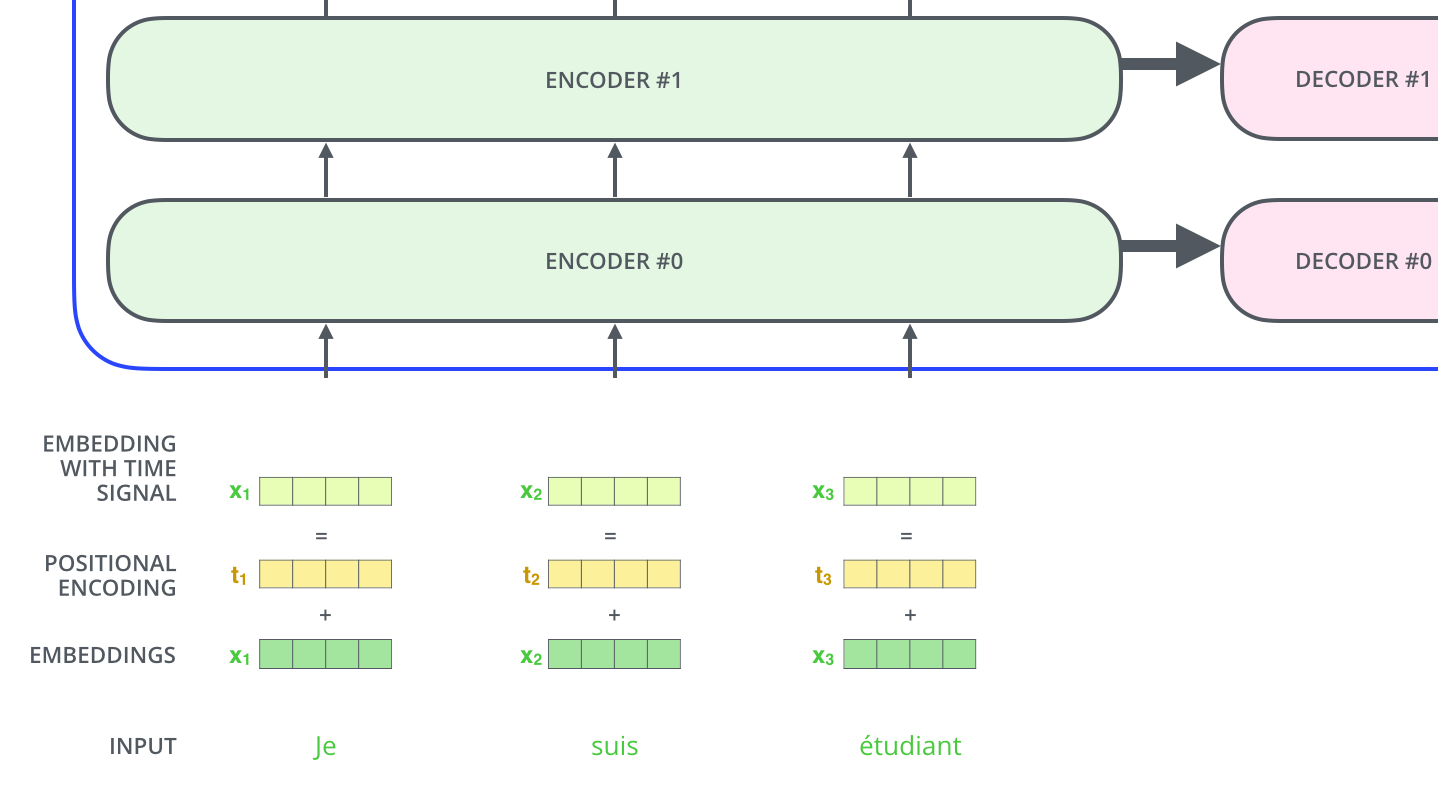
8. L’encodage positionnel

Une chose qui manque dans le modèle tel que nous l’avons décrit jusqu’à présent, est une façon de rendre compte de l’ordre des mots dans la séquence d’entrée.

Pour y remédier, le transformer ajoute un vecteur à chaque enchâssement d’entrée. Ces vecteurs suivent un forme particulière que le modèle apprend ce qui l’aide à déterminer la position de chaque mot (ou la distance entre les différents mots dans la séquence). L’intuition ici est que l’ajout de ces valeurs à l’enchâssement fournit des distances significatives entre les vecteurs d’enchâssement une fois qu’ils sont projetés dans les vecteurs Q/K/V (puis pendant l’application du produit scalaire).

Si nous supposons que l’enchâssement a une dimension de 4, les encodages positionnels ressembleraient à ceci :

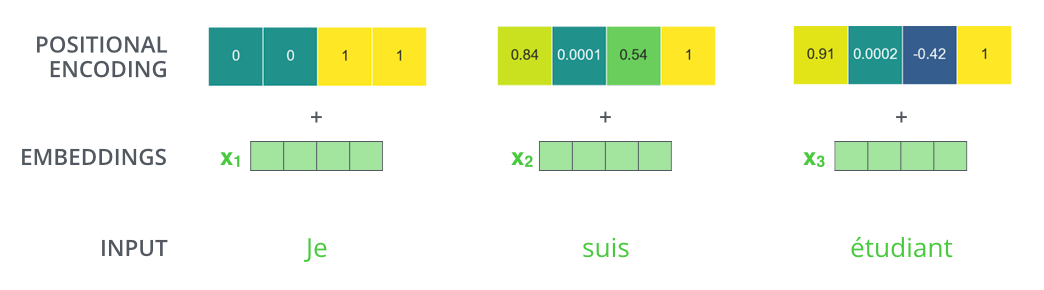
Dans la figure suivante, chaque ligne correspond à l’encodage positionnel d’un vecteur. Ainsi, la première ligne est le vecteur que nous ajoutons à l’enchâssement du premier mot dans une séquence d’entrée. Chaque ligne contient 512 valeurs, chacune ayant une valeur comprise entre 1 et -1. Nous les avons codés par couleur pour que le motif soit visible.

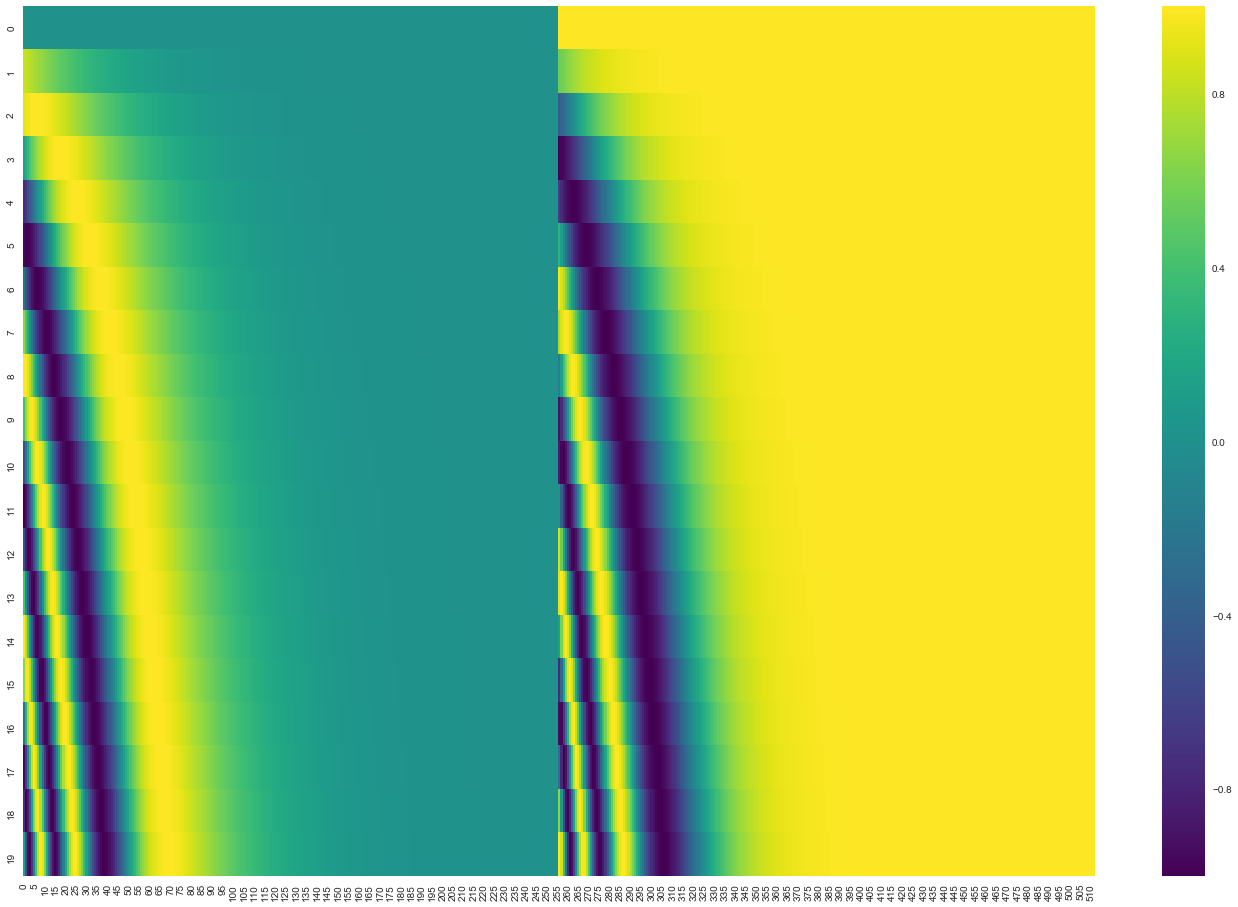
Un exemple réel d’encodage positionnel pour 20 mots (lignes) avec une taille d’enchâssement de 512 (colonnes). Vous pouvez voir qu’il semble divisé en deux au centre. C’est parce que les valeurs de la moitié gauche sont générées par une fonction (qui utilise le sinus), et la moitié droite est générée par une autre fonction (qui utilise le cosinus). Ils sont ensuite concaténés pour former chacun des vecteurs d’encodage positionnel.

La formule d’encodage positionnel est :

\[\text{PE}(i,\delta) = \begin{cases} \sin(\frac{i}{10000^{2\delta'/d}}) & \text{si } \delta = 2\delta'\\ \cos(\frac{i}{10000^{2\delta'/d}}) & \text{si } \delta = 2\delta' + 1\\ \end{cases}\]

avec i la position du token et delta la dimension.

Vous pouvez voir le code de génération des encodages positionnels dans get_timing_signal_1d().

Ce n’est pas la seule méthode possible pour l’encodage positionnel. Celle-ci offre cependant l’avantage de pouvoir s’adapter à des longueurs de séquences invisibles (par exemple, si notre modèle entrainé est appelé à traduire une phrase plus longue que n’importe laquelle de celles de notre série de séquences d’entraînement).


9. Les connexions résiduelles

Un détail de l’architecture de l’encodeur que nous devons mentionner avant de continuer est que chaque sous-couche (auto-attention, feed-forward) dans chaque codeur a une connexion résiduelle autour de lui (Add sur le graphique ci-dessous) et est suivie d’une étape de normalisation.

Si nous visualisons les vecteurs et l’opération de normalisation associée à l’auto-attention, cela ressemble à ceci :

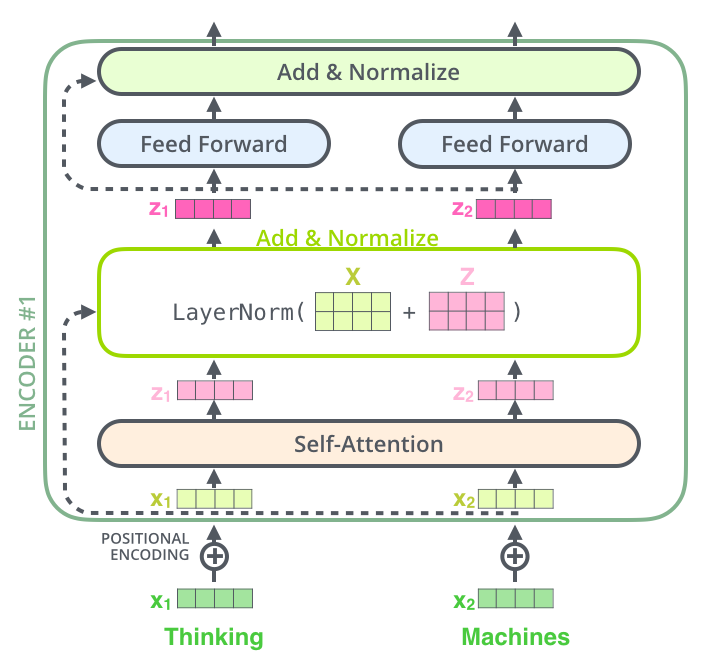
Les résidus sont représentés en pointillé et sont ajoutés avant la normalisation. 10% de dropout est appliqué à cette étape

Cela vaut également pour les sous-couches du décodeur.

Par exemple un transformer avec 2 encodeurs et décodeurs empilés ressemble à ceci :




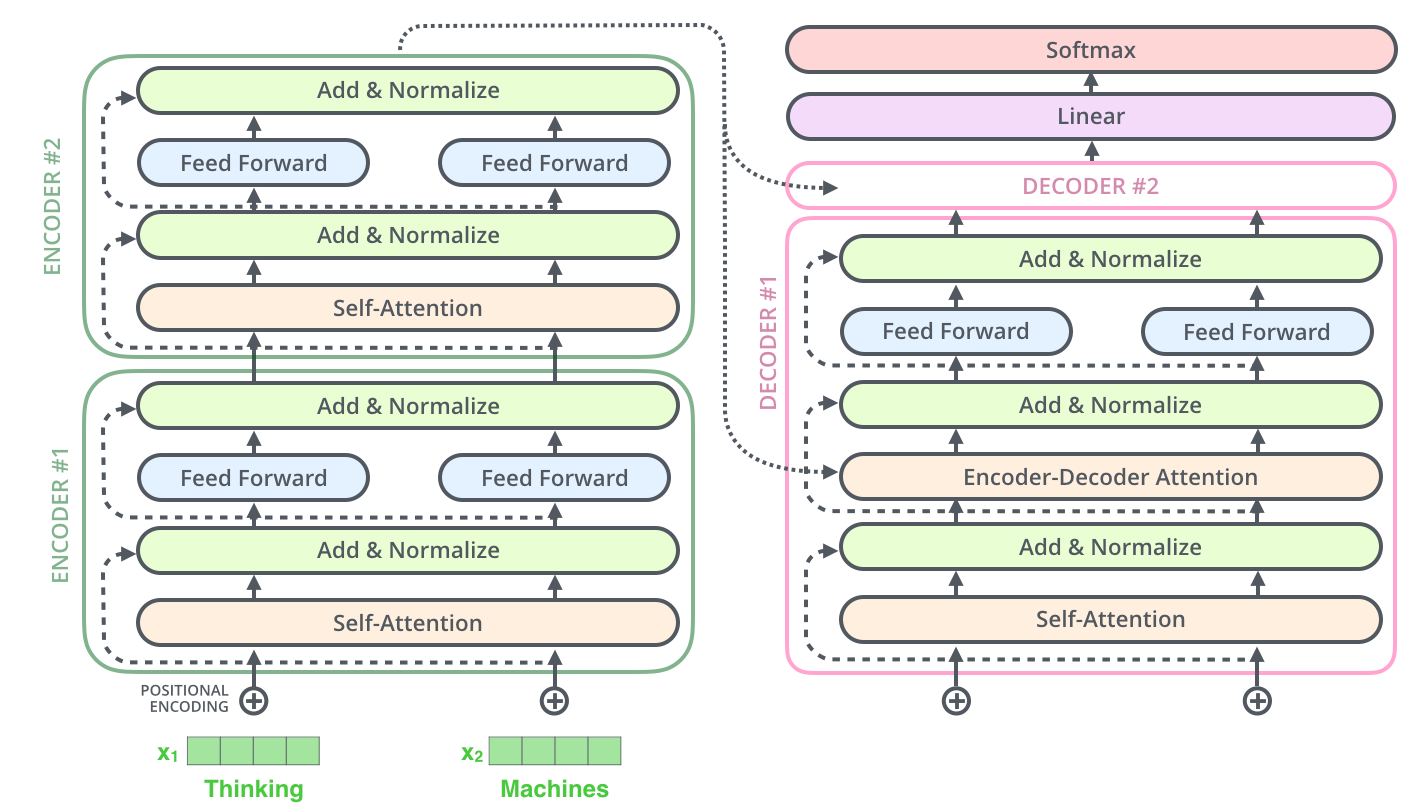
10. Le décodeur

Maintenant que nous avons couvert la plupart des concepts du côté des encodeurs et savons comment fonctionnent les composants des décodeurs, jetons un coup d’œil à la façon dont ils travaillent ensemble.

L’encodeur commence par traiter la séquence d’entrée. La sortie de l’encodeur supérieur est ensuite transformée en un ensemble de vecteurs d’attention K et V. Ceux-ci doivent être utilisés par chaque décodeur dans sa couche « attention encodeur-décodeur » qui permet au décodeur de se concentrer sur les endroits appropriés dans la séquence d’entrée :

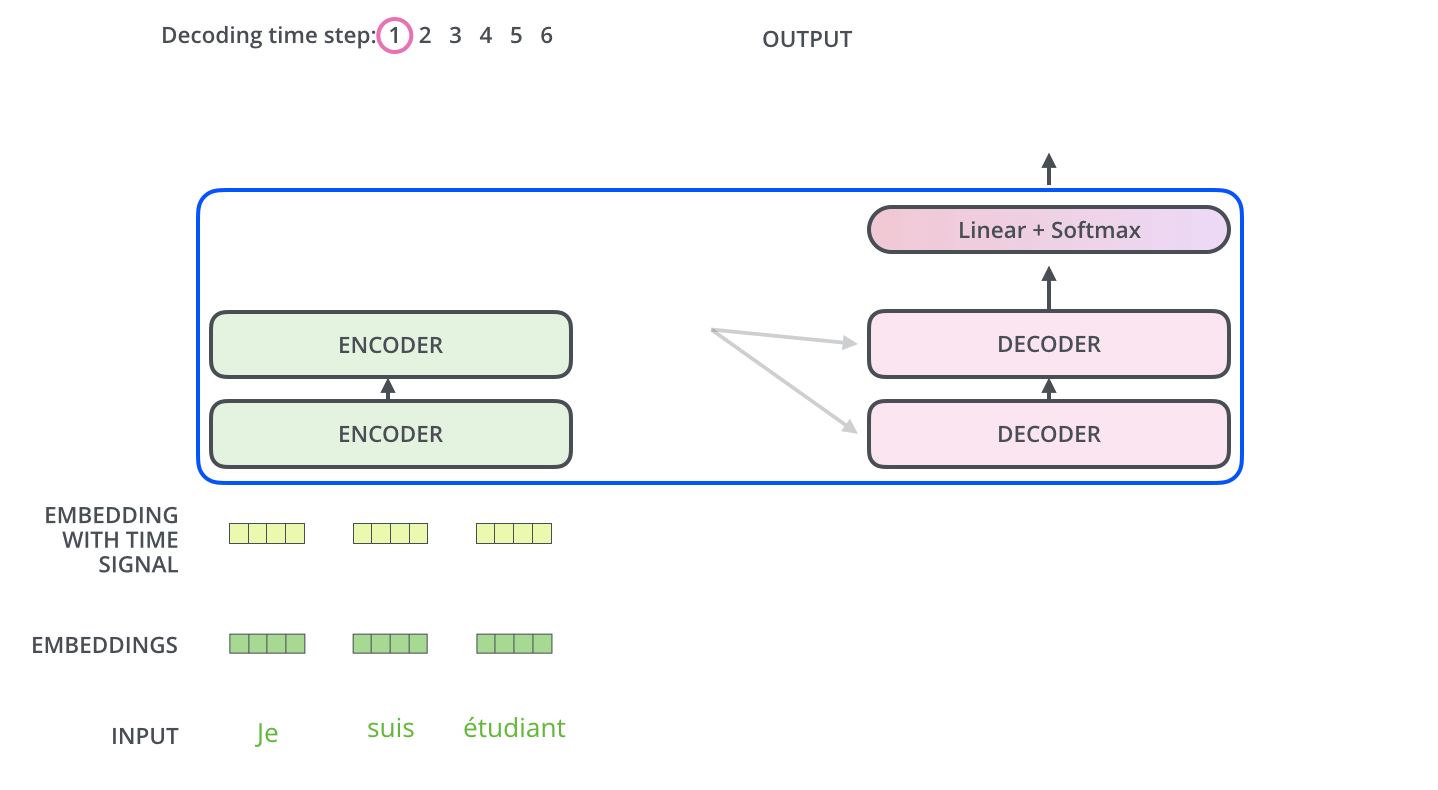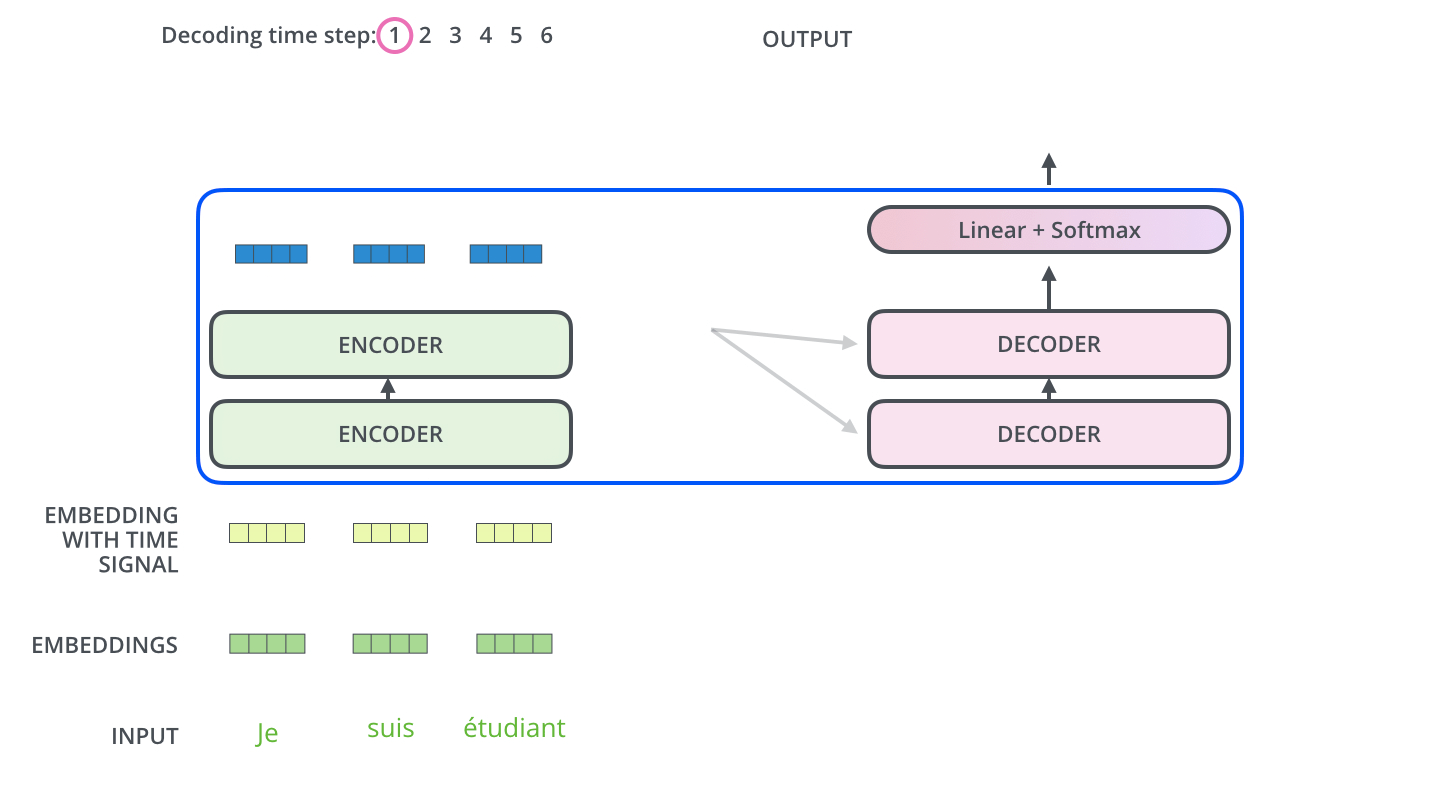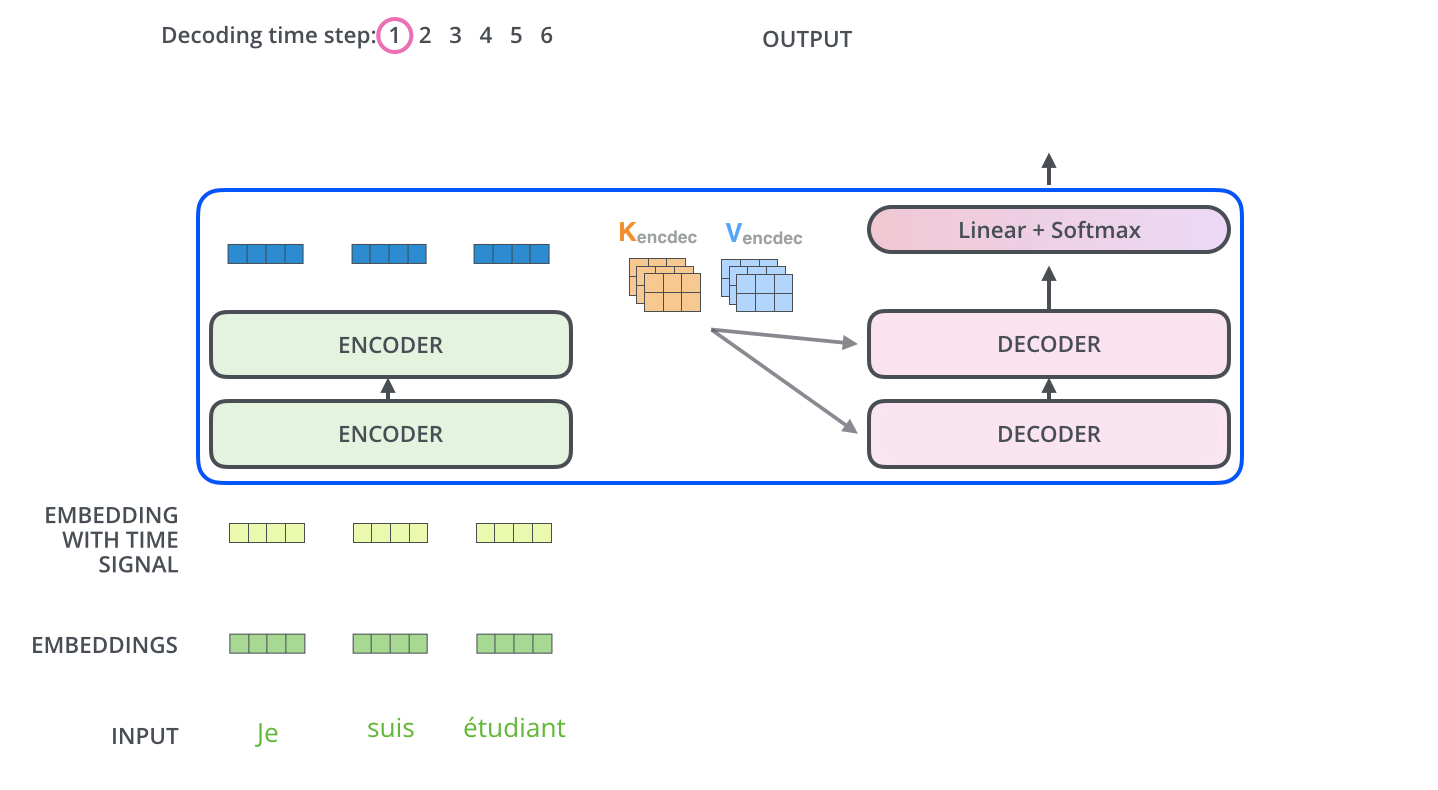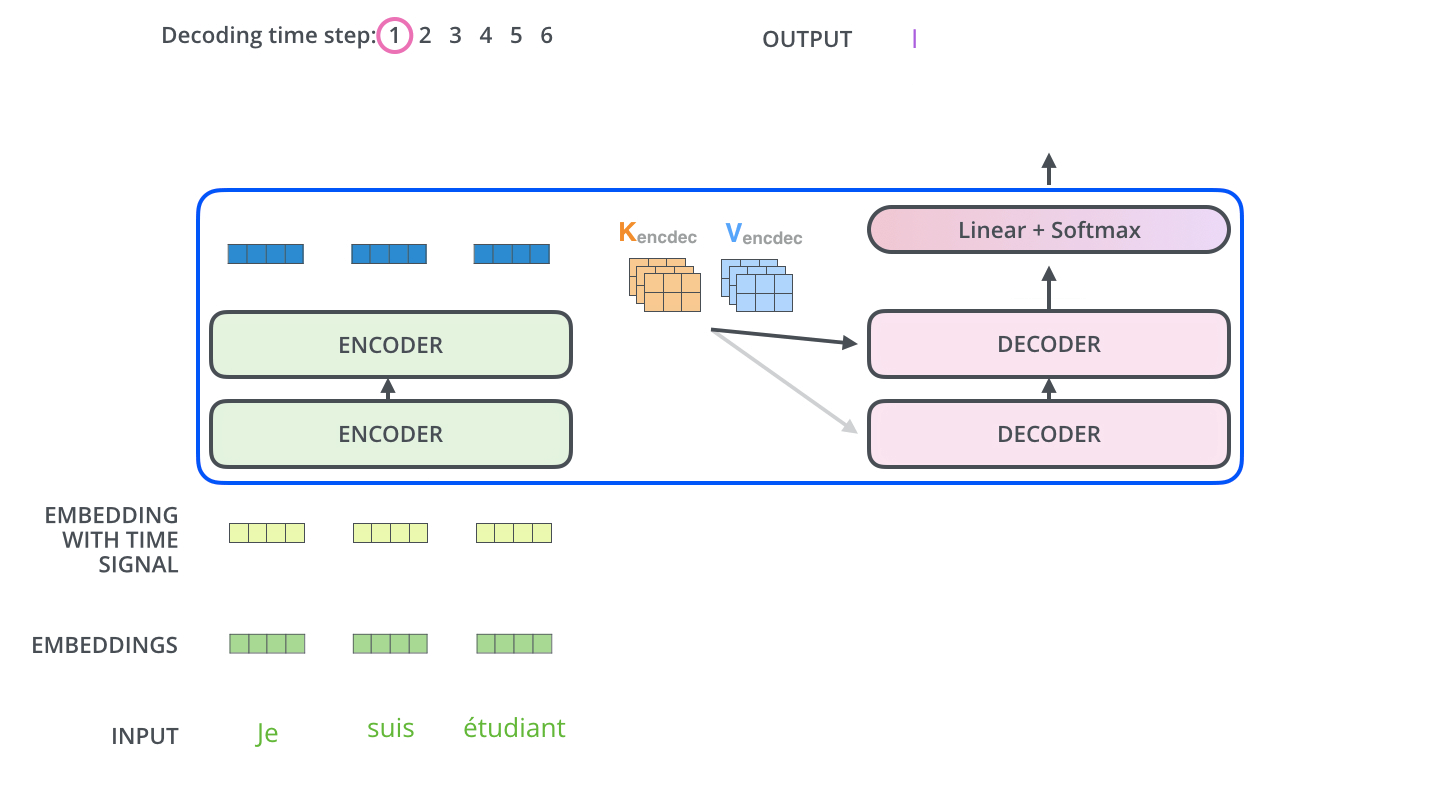
Après avoir terminé la phase d’encodage, nous commençons la phase de décodage. Chaque étape de la phase de décodage produit un élément de la séquence de sortie (la traduction en anglais dans ce cas).

Les étapes suivantes répètent le processus jusqu’à ce qu’un symbole spécial indique au décodeur que le transformer a complété entièrement la sortie. La sortie de chaque étape (mot ici) est envoyée au décodeur le plus bas pour le traitement du mot suivant. Et tout comme nous l’avons fait avec les entrées encodeur, nous enchâssons et ajoutons un codage positionnel à ces entrées décodeur pour indiquer la position de chaque mot.

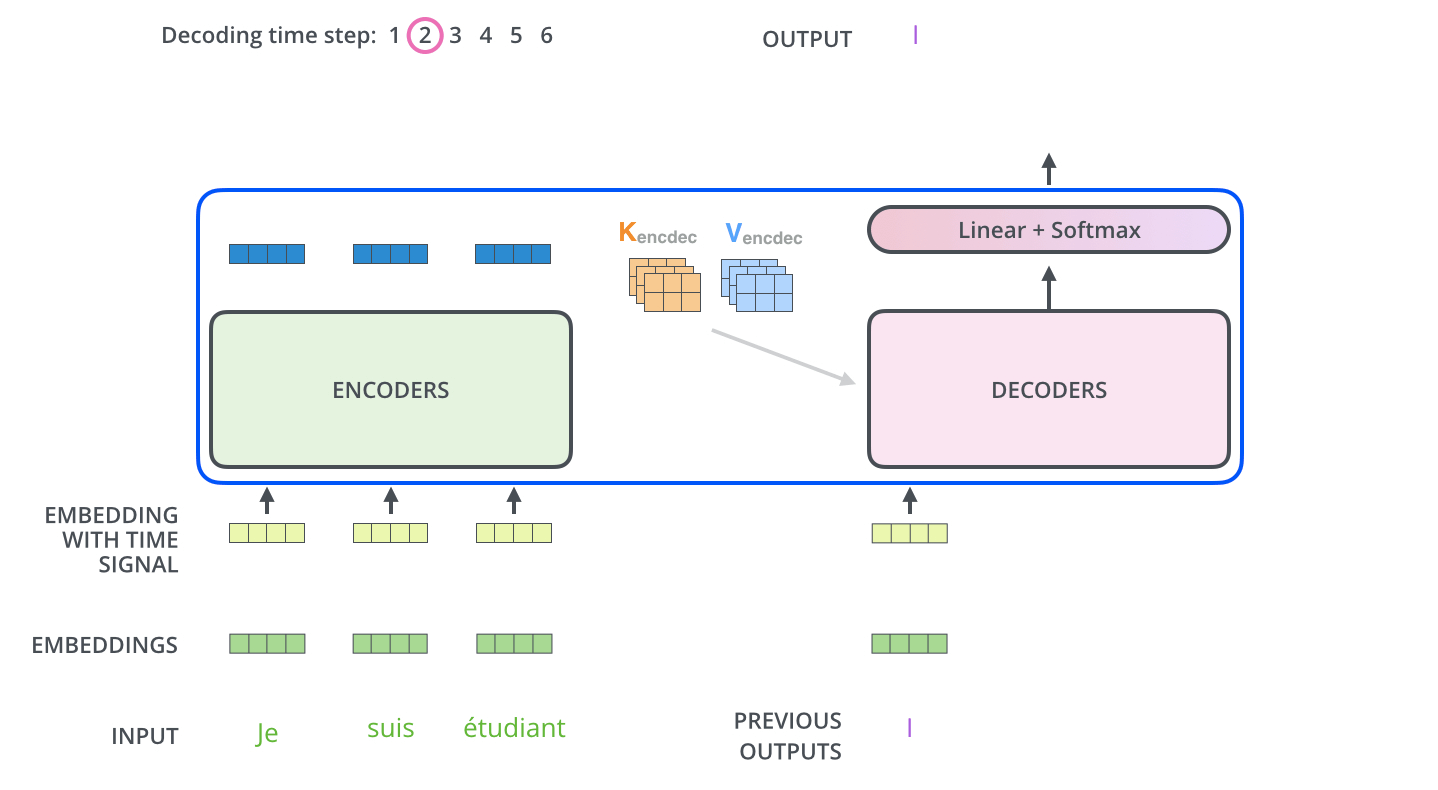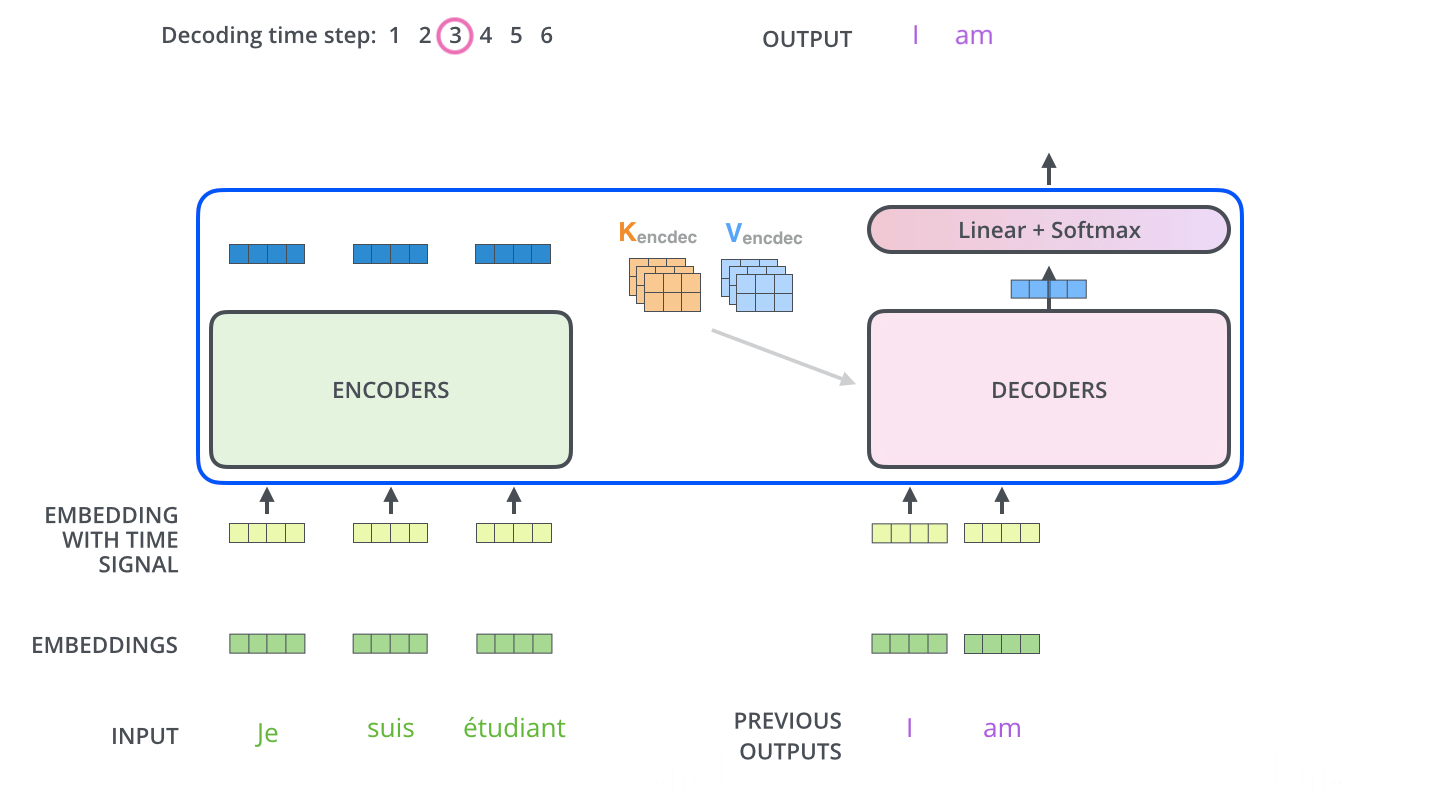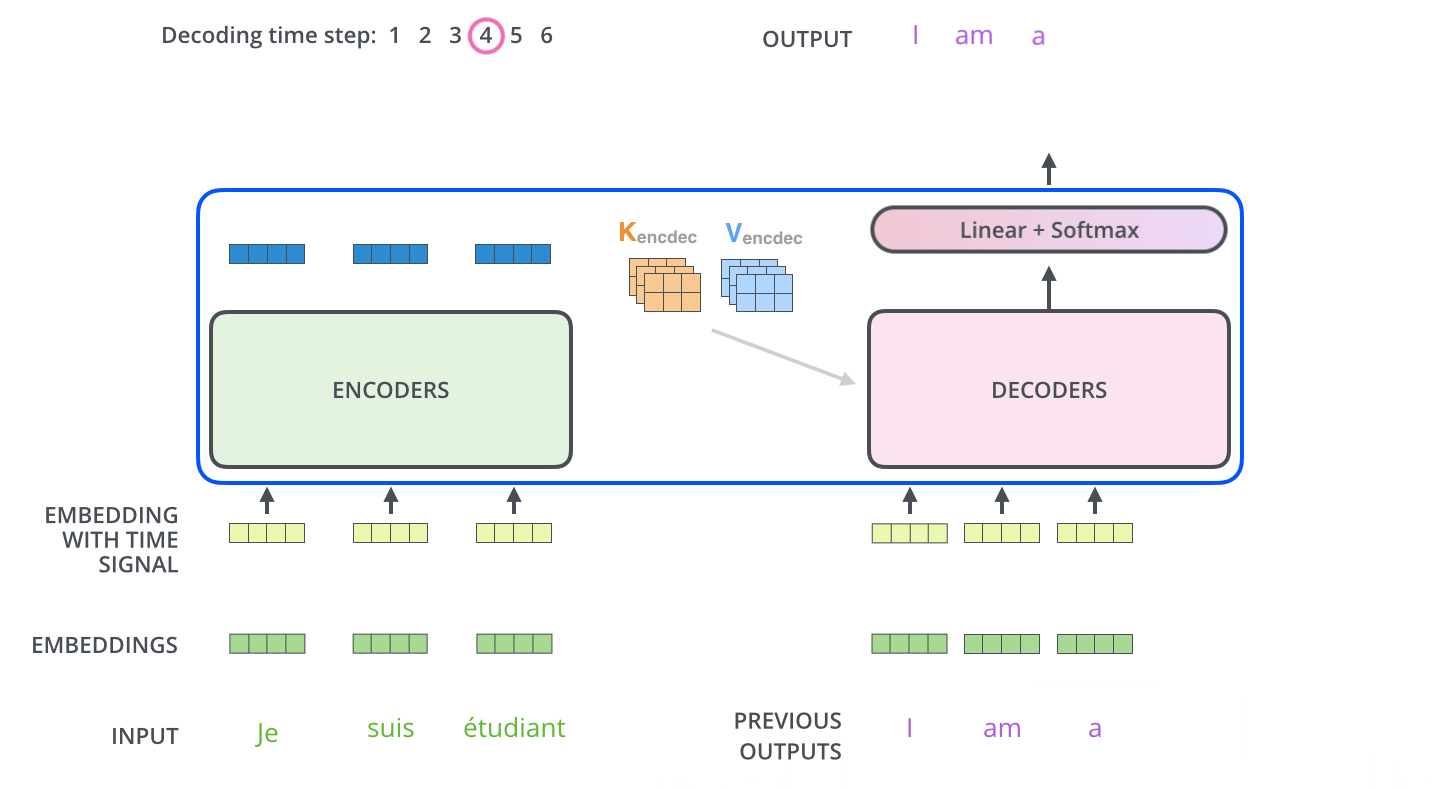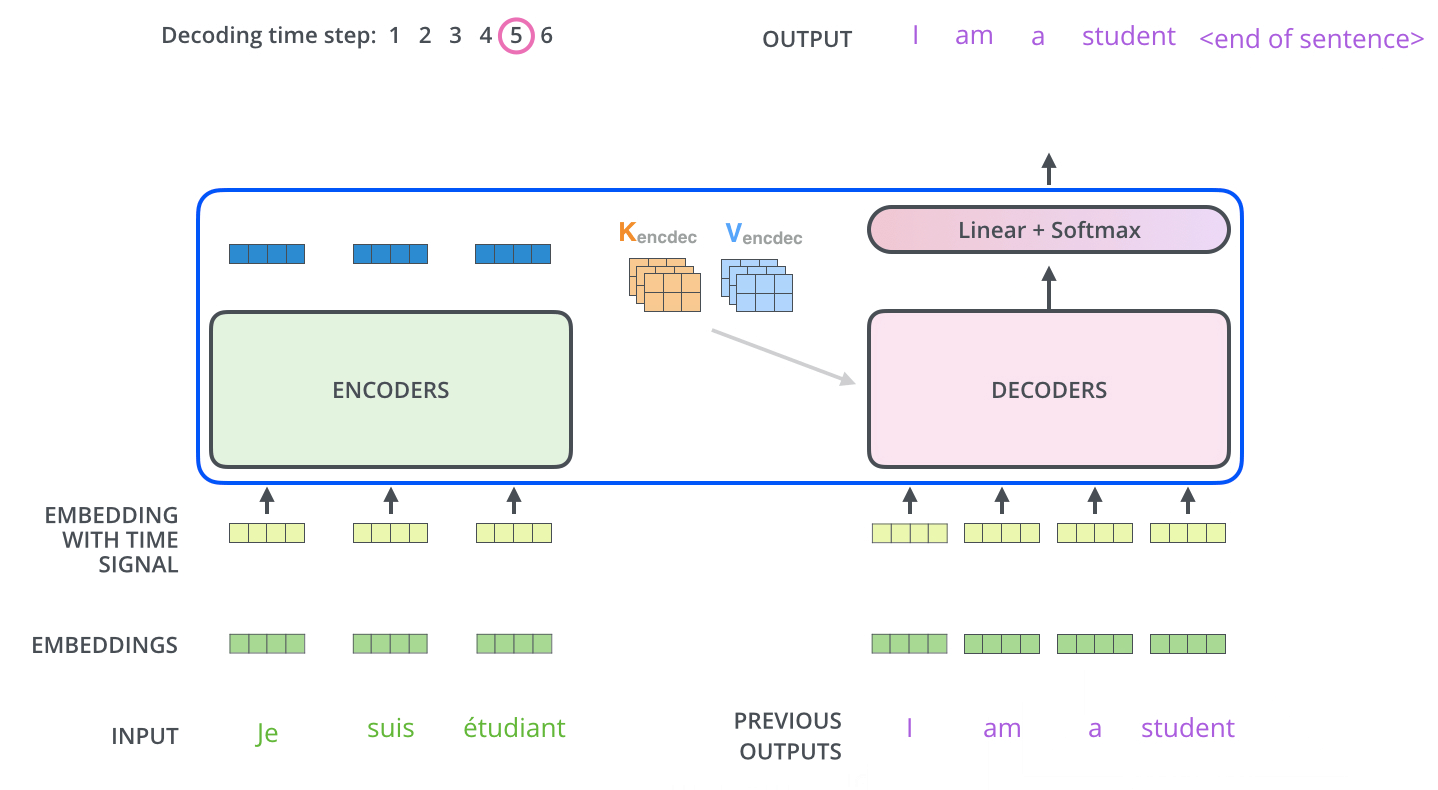
Après avoir terminé la phase d’encodage, nous commençons la phase de décodage. Chaque étape de la phase de décodage produit un élément de la séquence de sortie (la traduction en anglais dans ce cas).

Les couches d’auto-attention du décodeur fonctionnent d’une manière légèrement différente de celle de l’encodeur.

Dans le décodeur, la couche d’auto-attention ne peut s’occuper que des positions antérieures dans la séquence de sortie. Ceci est fait en masquant les positions futures (en les réglant sur -inf) avant l’étape softmax du calcul de l’auto-attention.

La couche « Attention encodeur-décodeur » fonctionne comme une auto-attention à plusieurs têtes, sauf qu’elle crée sa matrice de requêtes à partir de la couche inférieure et prend la matrice des clés et des valeurs à la sortie de la pile encodeur.


11. Les couches finales : linéaire et softmax

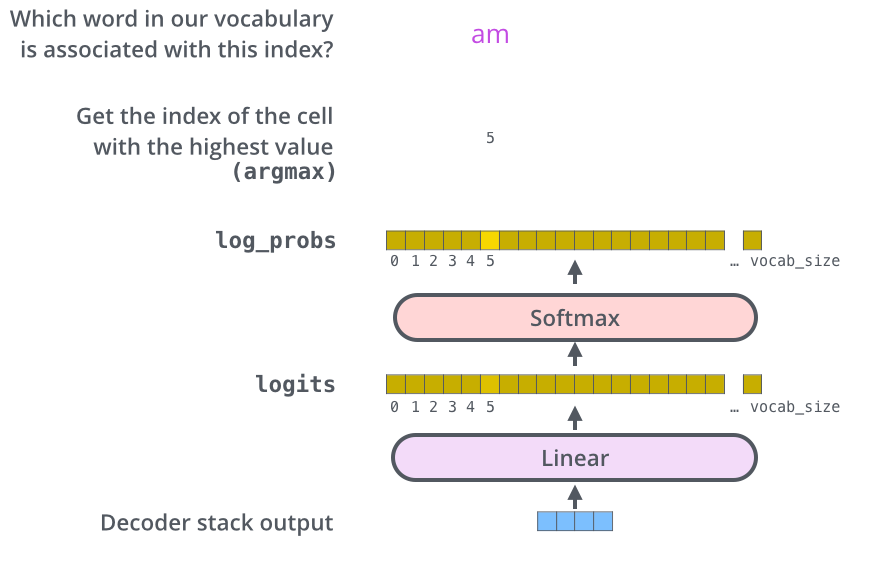
La pile de décodeurs délivre un vecteur de float. Comment le transformer en mots ? C’est le travail de la couche linéaire qui est suivie d’une couche softmax.

La couche linéaire est un simple réseau neuronal entièrement connecté qui projette le vecteur produit par la pile de décodeurs dans un vecteur beaucoup (beaucoup) plus grand appelé vecteur de logits.

Supposons que notre modèle connaisse 10 000 mots anglais uniques (le « vocabulaire de sortie » de notre modèle) qu’il a appris de son jeu de données d’entraînement. Cela rend le vecteur de logits large de 10 000 cellules, chaque cellule correspondant au score d’un mot unique. C’est ainsi que nous interprétons la sortie du modèle suivie de la couche linéaire.

La couche softmax transforme ensuite ces scores en probabilités (tous positifs et dont la somme vaut 1). La cellule ayant la probabilité la plus élevée est choisie et le mot qui lui est associé est produit comme sortie pour ce pas de temps.




12. L’entraînement

Maintenant que nous avons couvert l’ensemble du processus d’un transformer, il serait utile de jeter un coup d’œil à l’intuition de l’entraînement du modèle.

Pendant l’entraînement, un modèle non entraîné passe exactement par le même processus. Mais puisque nous l’entraînons sur un jeu de données d’entraînement labellisé, nous pouvons comparer sa sortie avec la sortie correcte réelle.

Pour visualiser ceci, supposons que notre vocabulaire de sortie ne contient que six mots (« a », « am », « i », « thanks », « student », et « ** »).

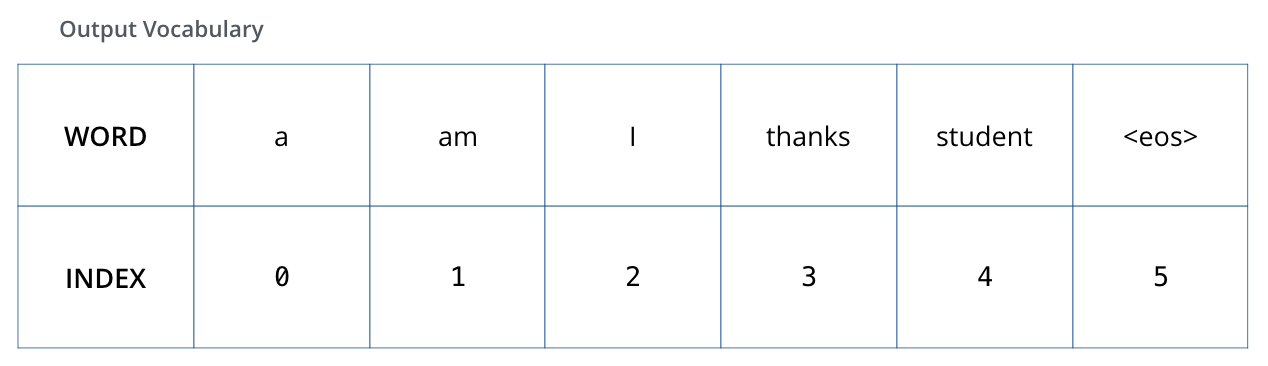
Une fois que nous avons défini notre vocabulaire de sortie, nous pouvons utiliser un vecteur de la même largeur pour indiquer chaque mot de notre vocabulaire. C’est ce qu’on appelle aussi le one-hot encoding. Ainsi, par exemple, nous pouvons indiquer le mot « am » à l’aide du vecteur suivant :

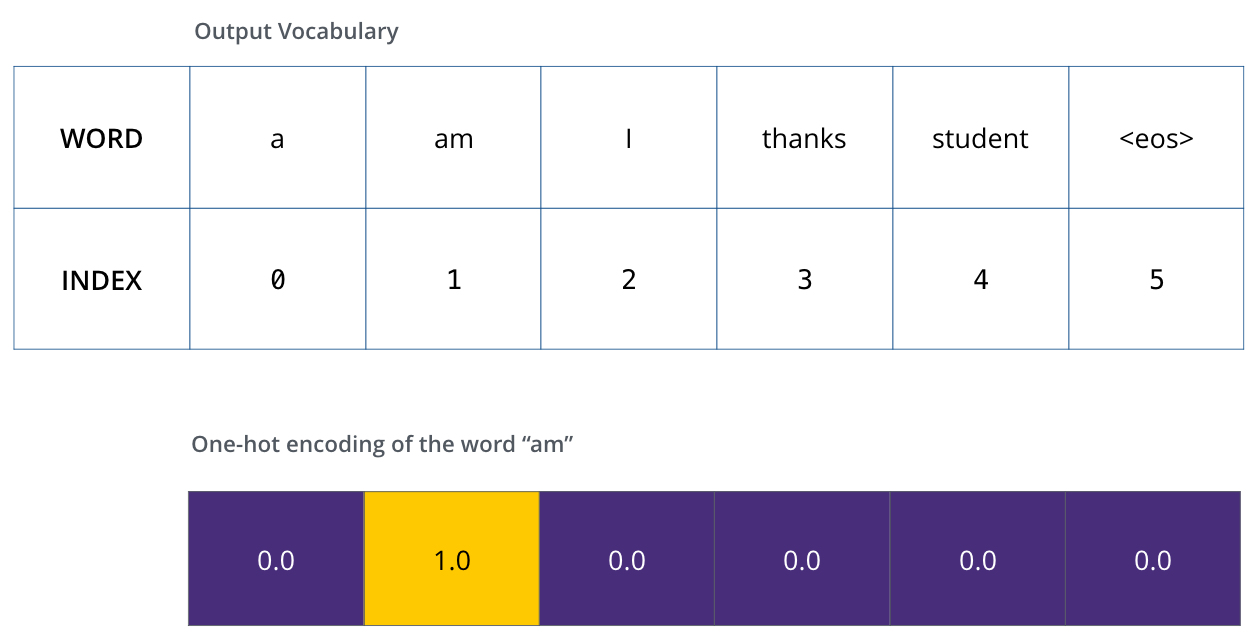
Après cette récapitulation, discutons de la fonction de perte du modèle, la métrique que nous optimisons pendant la phase d’entraînement.


13. La fonction de perte

Disons que nous sommes à la première étape de la phase d’entraînement et que nous souhaitons traduire « merci » en « thanks ». Ce que cela signifie, c’est que nous voulons que la sortie soit une distribution de probabilité indiquant le mot « merci ». Mais comme ce modèle n’est pas encore entraîné, il est peu probable que cela se produise tout de suite.

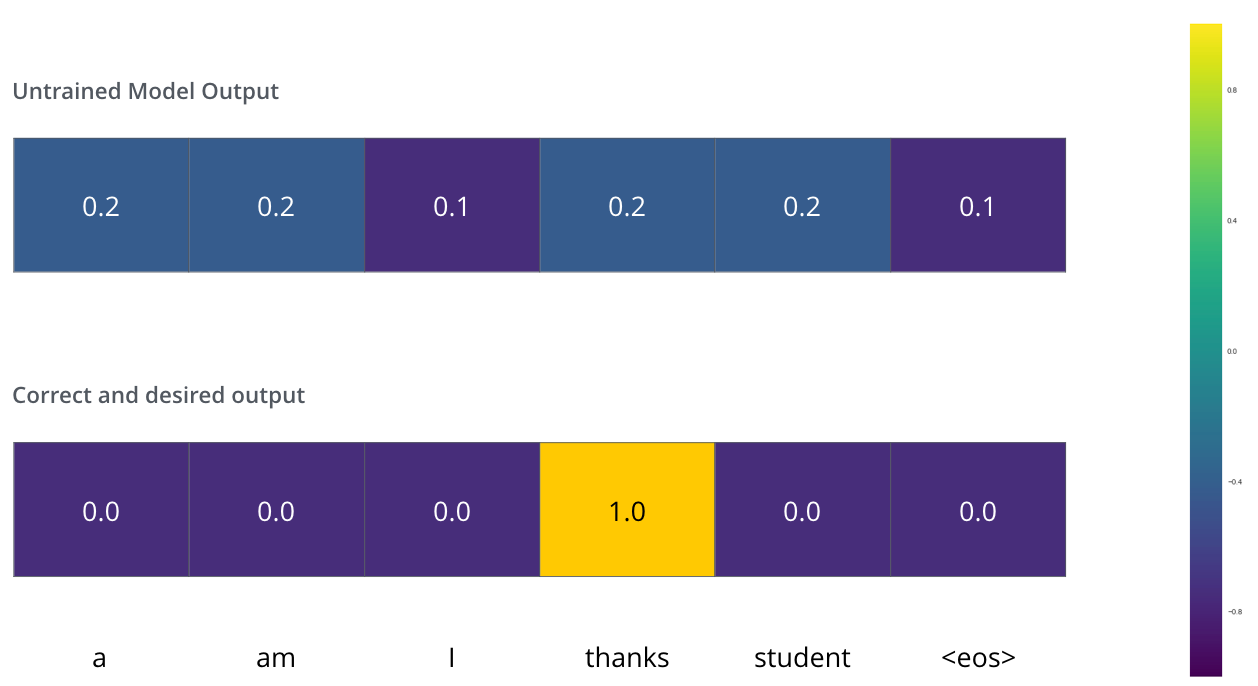
Comme les paramètres (poids) du modèle sont tous initialisés de façon aléatoire, le modèle (non entraîné) produit une distribution de probabilités avec des valeurs arbitraires pour chaque cellule/mot. Nous pouvons le comparer avec la sortie réelle, puis ajuster tous les poids du modèle à l’aide de la rétropropagation pour obtenir une sortie plus proche de la sortie souhaitée.

Comment comparer deux distributions de probabilités ? Nous soustrayons simplement l’une à l’autre. Pour plus de détails, voir l’entropie croisée et la divergence de Kullback-Leibler.

Mais notez qu’il s’agit d’un exemple très simplifié. De façon plus réaliste, nous utiliserons une phrase plutôt qu’un mot. Par exemple en entrée : « Je suis étudiant » et comme résultat attendu : « I am a student ». Ce que cela signifie vraiment, c’est que nous voulons que notre modèle produise successivement des distributions de probabilités où :

  • Chaque distribution de probabilité est représentée par un vecteur de largeur vocab_size (6 dans notre exemple, mais de façon plus réaliste un nombre comme 3 000 ou 10 000)
  • La première distribution de probabilités a la probabilité la plus élevée à la cellule associée au mot « I »
  • La deuxième distribution de probabilité a la probabilité la plus élevée à la cellule associée au mot « am »
  • Et ainsi de suite jusqu’à ce que la cinquième distribution de sortie indique ‘’, auquel est également associée une cellule du vocabulaire à 10 000 éléments
Résultat optimal

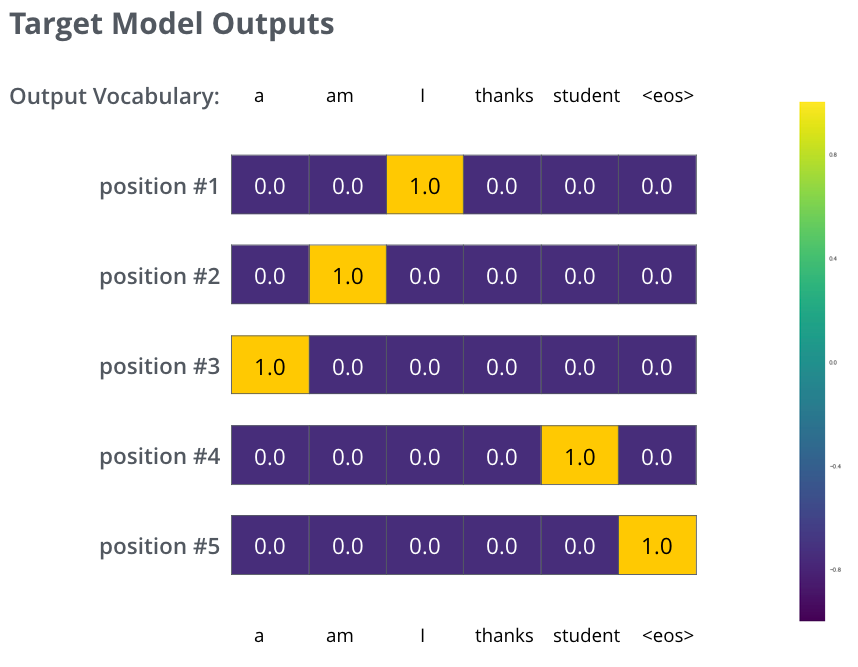
Après avoir entraîné le modèle pendant suffisamment de temps sur un jeu de données suffisamment grand, nous pouvons espérer un résultat semblable à celui-ci :

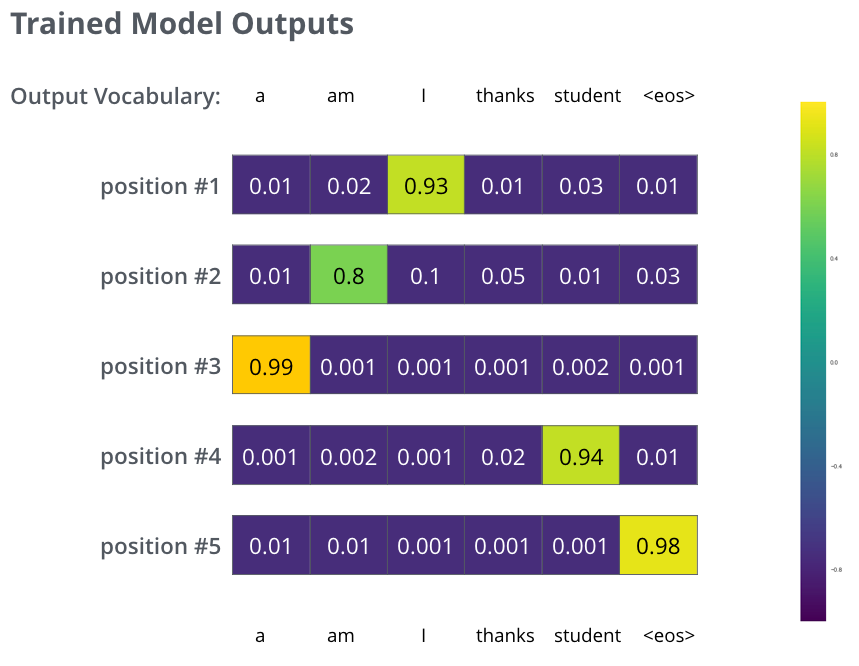
Comme le modèle produit les sorties une à une la fois, nous pouvons supposer que le modèle choisit le mot ayant la probabilité la plus élevée à partir de cette distribution de probabilité et jette le reste. C’est une façon de faire appellée greedy decoding (recherche gourmande).

Une autre façon de faire serait de s’accrocher, par exemple, aux deux premiers mots (disons, « I » et « a » par exemple), puis, à l’étape suivante, d’exécuter le modèle deux fois : une fois en supposant que la première position de sortie était le mot « I » , et une autre fois en supposant que la première position de sortie était « a ». La version la moins erronée étant retenue, en considérant les positions #1 et #2. Nous répétons ceci pour les positions #2 et #3, etc… Cette méthode est appelée « beam search » (recherche en faisceau).

Dans notre exemple, beam_size était deux (parce que nous avons comparé les résultats après avoir calculé les faisceaux pour les positions #1 et #2) et top_beams est aussi deux (puisque nous avons gardé deux mots). Ce sont deux hyperparamètres que vous pouvez expérimenter.


14. Pour aller plus loin

Lire l’article Attention Is All You Need (article original où est détaillé plus techniquement les paramètres utilisé pour les couches de normalisation, dropout, etc.), le transformer blog (Transformer: A Novel Neural Network Architecture for Language Understanding), et le Tensor2Tensor announcement.

Jouer avec le Jupyter Notebook de Tensor2Tensor et plus généralement explorer le GitHub Tensor2Tensor.

Des articles sur divers travaux utilisant les transformers :

Conclusion

L’architecture du transformer présentée dans cet article est une rupture technologique dans le domaine du traitement du langage naturel. ENORMEMENT d’autres modèles basés sur ce transformer de base ont été dévoilés depuis.
J’entre plus en détails pour deux d’entre eux que j’ai eu l’occasion d’utiliser professionnellement : BERT et le GPT2. Pour les autres architectures, vous pouvez consulter une liste non exhaustive dans cet article du blog.


Références

Citation

@inproceedings{transformer_blog_post,
author = {Loïck BOURDOIS},
title = {Illustration du Transformer},
year = {2019},
url = {https://lbourdois.github.io/blog/nlp/Transformer/}
}

Vous pourriez aimer aussi