Avant-propos

Cet article est une traduction de l’article de Alireza Dirafzoon : Illustrating the Reformer. Merci à lui de m’avoir autorisé à effectuer cette traduction. J’ai ajouté des éléments supplémentaires quand j’estimais que cela était pertinent.


Introduction

Récemment, Google a introduit l’architecture Reformer, un modèle de transformer conçu pour traiter efficacement de très longues séquences de données (par exemple jusqu’à 1 million de mots). L’exécution de reformer nécessite une consommation de mémoire beaucoup plus faible que les transformers classiques et permet d’obtenir des performances impressionnantes en utilisant un seul GPU. La publication Reformer : The efficient Transformer de Kitaev, Kaiser et Levskaya sera officiellement présentée au ICLR 2020 mais est déjà actuellement disponible en open review. Le modèle reformer devrait avoir un impact significatif en allant au-delà des applications linguistiques (par exemple, la génération de musique, de parole, d’images et de vidéos).

Avant de poursuivre cet article, sachez que le Reformer est une version optimisée du Transformer de Vaswani et al. Ainsi, si vous n’êtes pas familier avec dernier lisez d’abord l’article du blog qui lui est consacré : Illustration du transformer.


1. Le reformer à la rescousse des problèmes du transformer

Les modèles de transformers (BERT et ses dérivés, le GPT2, etc.) donnent de bons résultats mais beaucoup de ces modèles ne peuvent être entraînés que sur de grandes plateformes de calcul industrielles et ne peuvent pas être affinés sur un seul GPU pour certaines en raison de leurs besoins en mémoire. Par exemple, le modèle GPT-2 complet se compose d’environ 1,5 milliard de paramètres.
Le reformer apporte une solution à ce problème en modifiant la manière dont sont effectués les calculs à plusieurs endroits du transformer.
Regardons ces modifications plus en détails. Voici une version simplifiée du transformer :

Résumé simplifié du transformer


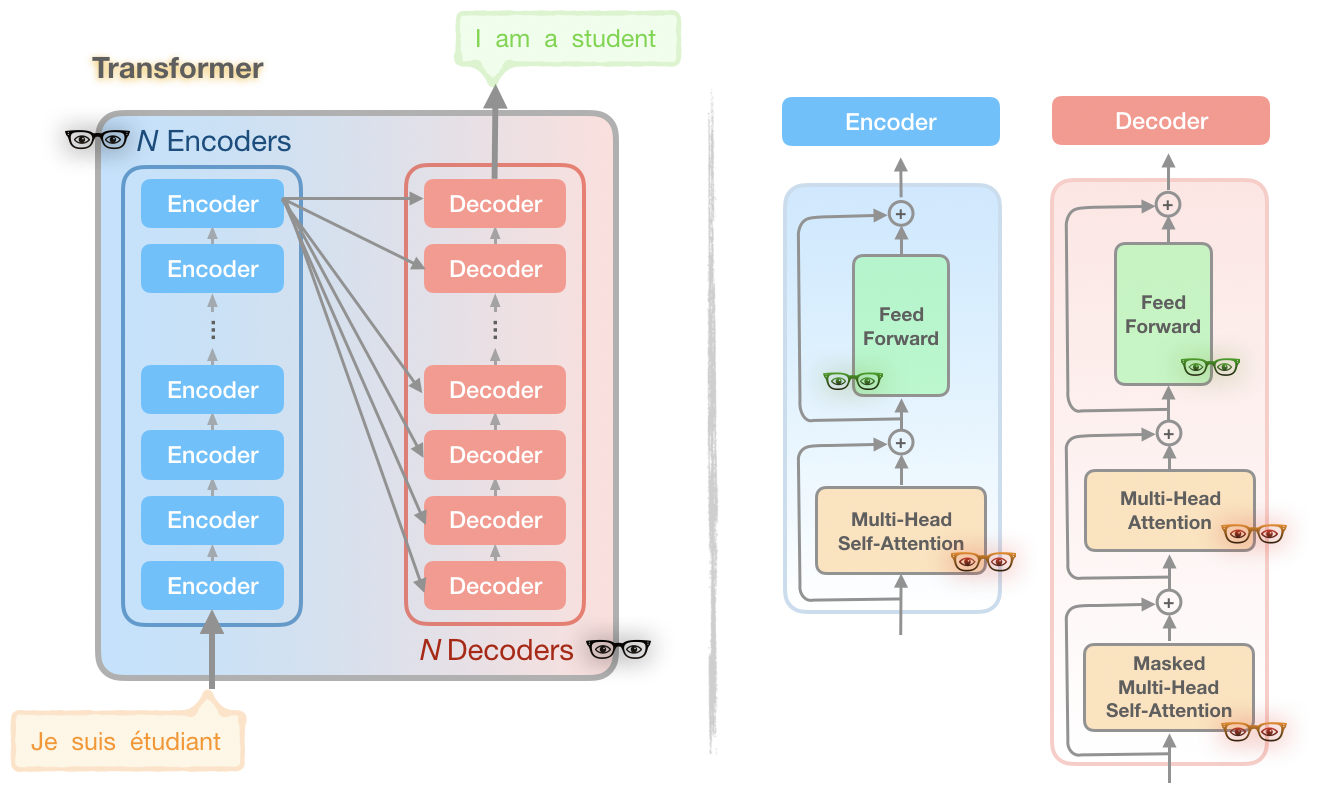
Sur le schéma ci-dessus, des logos de lunettes de 3 couleurs différentes sont présents. Chacun de ces logos représente une partie du modèle du transformer que les auteurs de reformer ont considéré comme une source de problèmes de calcul et de mémoire :

  • Problème 1 (lunettes rouges) : le calcul de l’attention
    Calculer l’attention sur des séquences de longueur L est de complexité O(L²) (à la fois temps et mémoire). Imaginez ce qui se passe si nous avons une séquence de longueur 64K.

  • Problème 2 (lunettes noires) : le nombre de couches
    Un modèle à N couches consomme N fois plus de mémoire qu’un modèle à une seule couche car les activations dans chaque couche doivent être stockées pour la rétropropagation.

  • Problème 3 (lunettes vertes) : la profondeur des couches feed-forward
    La profondeur des couches feed-forward intermédiaires est souvent beaucoup plus importante que la profondeur des activations de l’attention.

Le modèle reformer s’attaque aux trois principales sources de consommation de mémoire du transformer mentionnées ci-dessus et les améliore de telle sorte que le modèle reformer peut gérer des fenêtres contextuelles allant jusqu’à un million de mots, le tout sur un seul GPU de seulement 16Go de mémoire. Pour cela, le modèle Reformer combine deux techniques pour résoudre les problèmes d’attention et d’allocation de mémoire : le locality-sensitive-hashing (LSH) pour réduire la complexité de l’attention sur de longues séquences, et les couches résiduelles réversibles pour utiliser plus efficacement la mémoire disponible. Détaillons ces deux techniques.


2. L’Attention LSH (Locality sensitive hashing)

Penchons-nous sur le premier problème soulevé : le calcul de l’attention.

2.1 Attention et voisins les plus proches

En NLP, l’attention est un mécanisme qui permet au réseau de se concentrer attentivement sur différentes parties d’un contexte en fonction de leur relation avec l’étape temporelle traitée. Il existe 3 types de mécanisme d’attention dans le modèle de transformer comme ci-dessous :

Image provenant de la présentation de Łukasz Kaiser


Dans le transformer, l’attention est calculée via le produit scalaire, formulé comme :

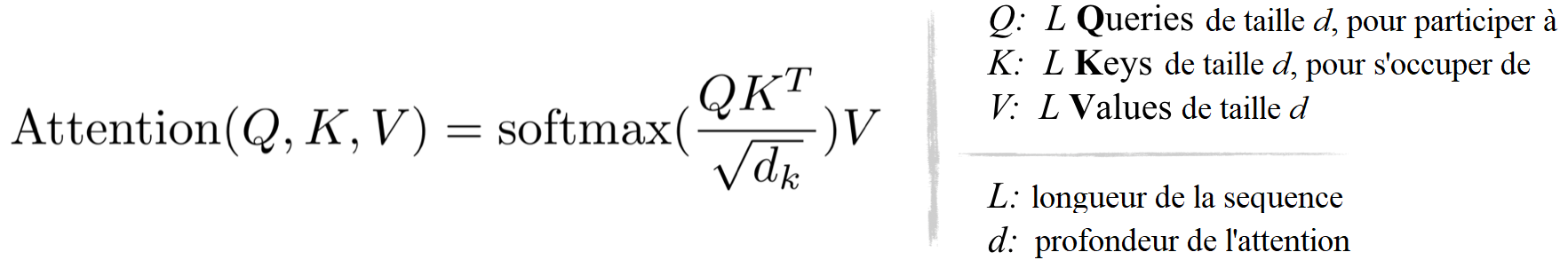
Pour l'ensemble de l'article nous adoptons la notation anglo-saxonne de la transposée


D’après l’équation ci-dessus et la figure ci-dessous, on peut observer que les coûts de calcul et de mémoire de la multiplication QKᵀ sont tous deux en O(L²), qui est le principal goulot d’étranglement de la mémoire.

Est-il nécessaire de calculer et de stocker la matrice complète QKᵀ ? La réponse est non, car nous ne sommes intéressés que par softmax(QKᵀ), qui est dominé par les éléments les plus grands d’une matrice éparse. Par conséquent, pour chaque requête q, nous ne devons prêter attention qu’aux clés k qui sont les plus proches de q. Par exemple, si K a une longueur de 64K, pour chaque q, nous ne pourrions considérer qu’un petit sous-ensemble des 32 ou 64 clés les plus proches. Le mécanisme d’attention du transformer trouve les clés les plus proches d’une requête, mais de manière inefficace.

La première nouveauté du reformer vient du remplacement de l’attention via le calcul du produit scalaire par un locality-sensitive hashing (hachage sensible à la localité) que l’on résumera par la suite par LSH. Cette transformation permet de passer d’une complexité de O(L²) à O(L log L).

2.2 Recherche des voisins les plus proches par LSH

LSH est un algorithme permettant une recherche efficace et approximative des voisins les plus proches dans des ensembles de données de grandes dimensions. L’idée principale de LSH est de sélectionner des fonctions de hachage telles que pour deux points « p » et « q », si « q » est proche de « p », alors avec une probabilité suffisante nous avons « hash(q) == hash(p) ».

2.2.1 L’approche basique

Le moyen le plus simple est de continuer à découper l’espace par des hyperplans aléatoires et d’ajouter sign(pᵀH) comme code de hachage de chaque point. Voyons un exemple ci-dessous :


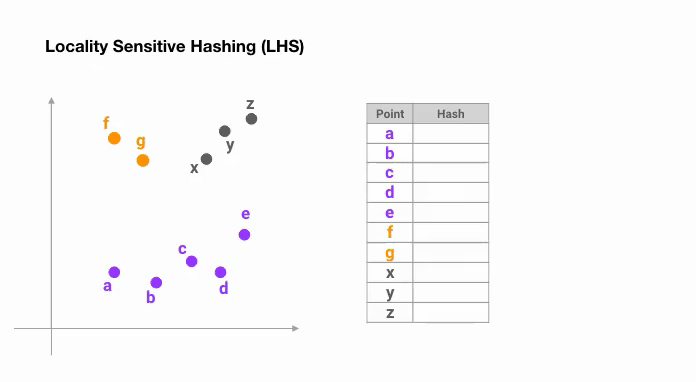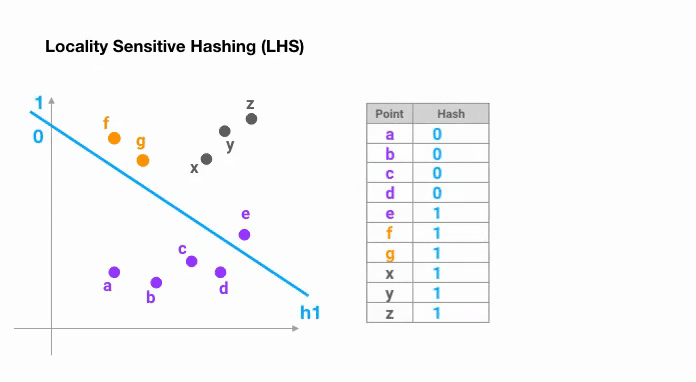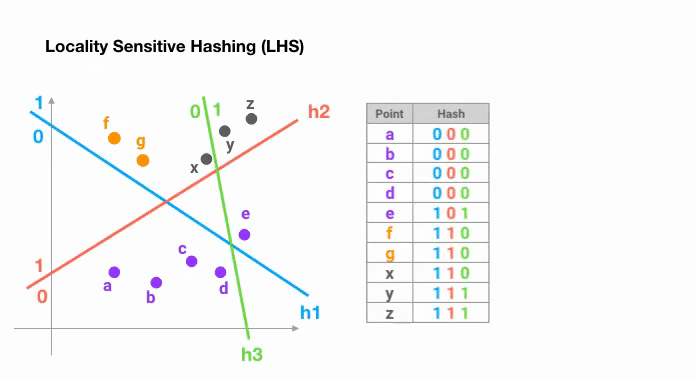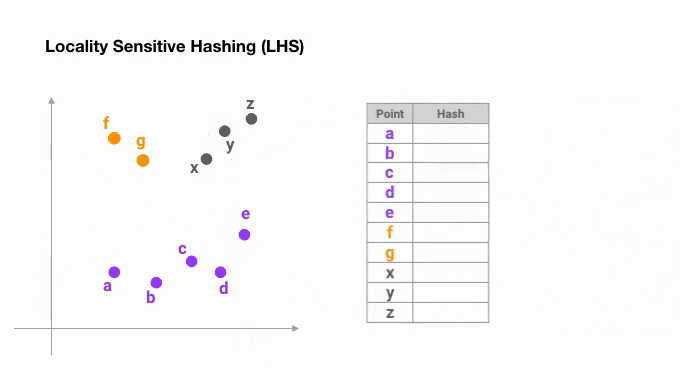
Une fois que nous avons trouvé des codes de hachage d’une longueur souhaitée, nous divisons les points en groupes en fonction de leurs codes de hachage. Dans l’exemple ci-dessus, « a » et « b » appartiennent au même groupe puisque hash(a) == hash(b). Maintenant, l’espace de recherche pour trouver les voisins les plus proches de chaque point se réduit considérablement, passant de l’ensemble des données au groupe auquel il appartient.

2.2.2 L’approche angulaire

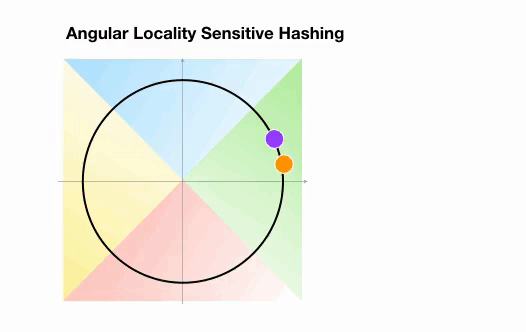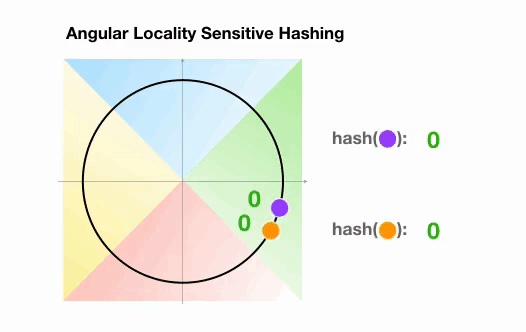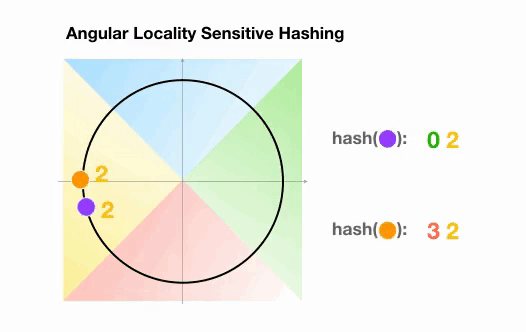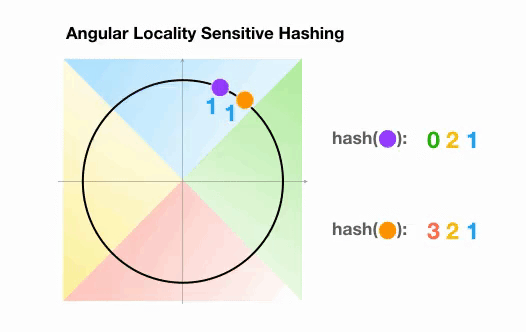
Une variante de l’algorithme LSH simple, appelée LSH angulaire, projette les points sur un cercle unité qui a été divisé en régions prédéfinies, chacune avec un code distinct. Ensuite, une série de rotations aléatoires des points définit le groupe auquel les points appartiennent. Illustrons cela par un exemple simplifié en 2D, tiré de l’article de reformer :

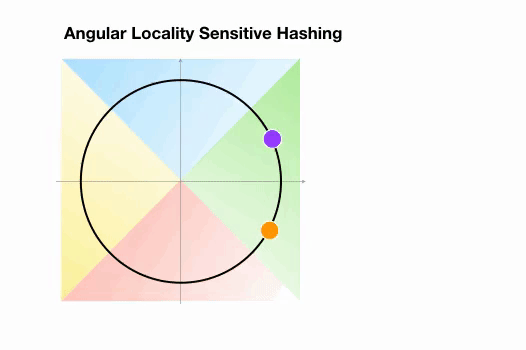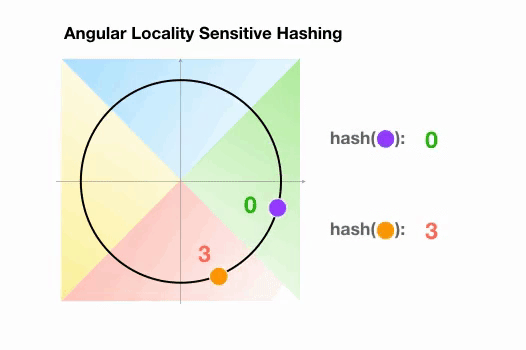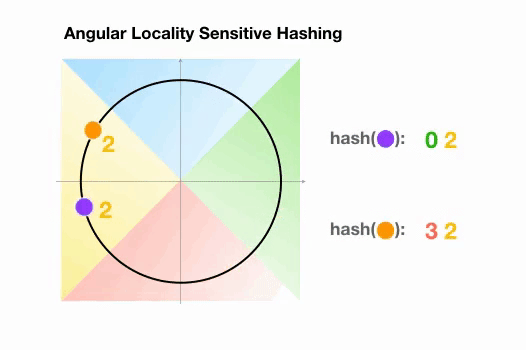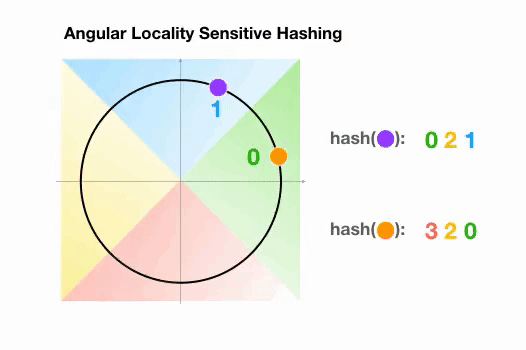
Ici, nous avons deux points qui sont projetés sur un cercle unité et tournés aléatoirement 3 fois avec des angles différents. On peut observer qu’il est peu probable qu’ils partagent le même groupe de hachage.

Dans l’exemple suivant, cependant, nous voyons que les deux points qui sont assez proches l’un de l’autre finiront par partager le même groupe de hachage après 3 rotations aléatoires :

2.3 Visualisation de l’attention LSH

Si l’on se réfère à la formule d’attention standard, au lieu de calculer l’attention sur tous les vecteurs des matrices Q et K, nous faisons ce qui suit :

  • Trouver les hachages LSH des matrices Q et K.
  • Calculer l’attention standard uniquement pour les vecteurs k et q dans les mêmes groupes de hachage. On répète ensuite la procédure ci-dessus plusieurs fois pour augmenter la probabilité que des éléments similaires ne tombent pas dans des groupes différents (les auteurs détaillent ce calcul dans l’appendix de leur article).

L’animation ci-dessous illustre une version simplifiée de l’attention LSH basée sur la figure de l’article du reformer :

2.4 L’attention LSH masquée

Pour mettre en œuvre l’attention LSH masquée, les auteurs associent chaque vecteur requête/clé à un indice de position, réorganisent les indices de position en utilisant les mêmes permutations que celles utilisées pour trier les vecteurs requête/clé, puis utilisent une opération de comparaison pour calculer le masque.

Alors que calculer l’attention d’un token futur n’est pas autorisée, les implémentations typiques du transformer permettent à une position de s’occuper d’elle-même.
Un tel comportement n’est pas souhaitable dans une formulation QK-partagé car le produit scalaire d’un vecteur requête avec lui-même sera presque toujours plus grand que le produit scalaire d’un vecteur requête avec un vecteur à une autre position. Les auteurs modifient donc le masquage pour interdire à un token de s’occuper de lui-même, sauf dans les situations où un token n’a pas d’autres cibles d’attention valables (par exemple, le premier token d’une séquence).


3. Transformer réversible et découpage

Regardons à présent le deuxième et le troisième problème du transformer, c’est-à-dire le nombre de couches d’encodeur et de décodeur, et la profondeur des couches feed-forward.

3.1 Réseau résiduel réversible (RevNet)

En observant attentivement les blocs d’encodeur et de décodeur du transformer (la figure avec les lunettes), on se rend compte que chaque couche d’attention et chaque couche feed-forward est enveloppée dans un bloc résiduel (partie gauche de la figure en dessous). Les réseaux résiduels (ResNets) présentés dans cet article par He et al. sont des composants puissants utilisés pour aider à résoudre le problème de la disparition du gradient dans les réseaux profonds (avec de nombreuses couches). Cependant, la consommation de mémoire dans les ResNets est un goulot d’étranglement car il faut stocker en mémoire les activations de chaque couche afin de calculer les gradients lors de la rétropropagation. Le coût de la mémoire est proportionnel au nombre d’unités dans le réseau.

Pour résoudre ce problème, on peut utiliser le réseau résiduel réversible (RevNet) de Gomez et Ren qui est composé d’une série de blocs réversibles. Dans le Revnet, les activations de chaque couche peuvent être reconstruites exactement à partir des activations de la couche suivante, ce qui nous permet d’effectuer une rétropropagation sans stocker les activations en mémoire. La figure ci-dessous illustre les blocs résiduels et les blocs résiduels réversibles. Notez comment nous pouvons calculer les entrées du bloc (X₁, X₂) à partir de ses sorties (Y₁, Y₂).


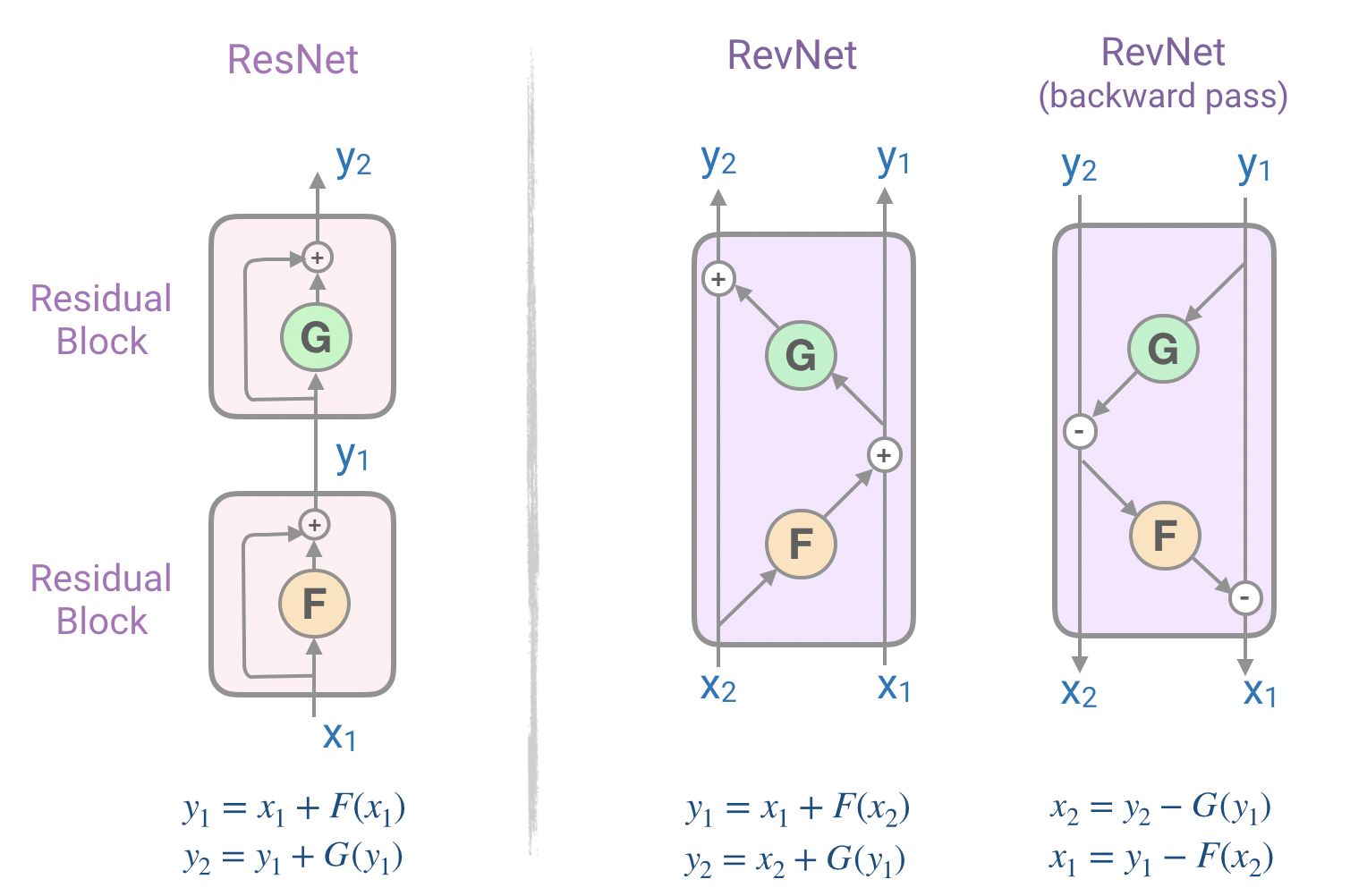
3.2 Transformer réversible

Pour traiter notre deuxième problème, le reformer applique l’idée du RevNet au transformer en combinant les couches d’attention et de feed-forward à l’intérieur du bloc RevNet. Dans la figure ci-dessus, F devient une couche d’attention et G la couche feed-forward et on a alors :
Y₁ = X₁ + Attention(X₂),
Y₂ = X₂ + FeedForward(Y₁)

L’utilisation de couches résiduelles réversibles au lieu de couches résiduelles standard permet désormais de ne stocker les activations qu’une seule fois pendant le processus d’entraînement au lieu de N fois.

3.3 Découpage

La dernière partie des améliorations apportées par le reformer porte sur le troisième problème, à savoir les vecteurs intermédiaires de grandes dimensions des couches feed-forward (pouvant aller jusqu’à des dimensions de 4000 et plus).

Comme les calculs des couches feed-forward sont indépendants entre les positions d’une séquence, les calculs des propagations avant et arrière ainsi que le calcul inverse peuvent tous être divisés en morceaux. Par exemple pour la propagation vers l’avant on a :



4. Résultats expérimentaux

Les auteurs ont mené des expériences sur deux tâches : la tâche de génération d’images imagenet64 (avec des séquences de longueur 12K) et la tâche de texte enwik8 (avec des séquences de longueur 64K), et ont évalué les effets des modifications sur la mémoire, la précision et la vitesse.

Les résultats de leur expérience ont montré que le transformer réversible permet d’économiser la mémoire sans sacrifier la précision :

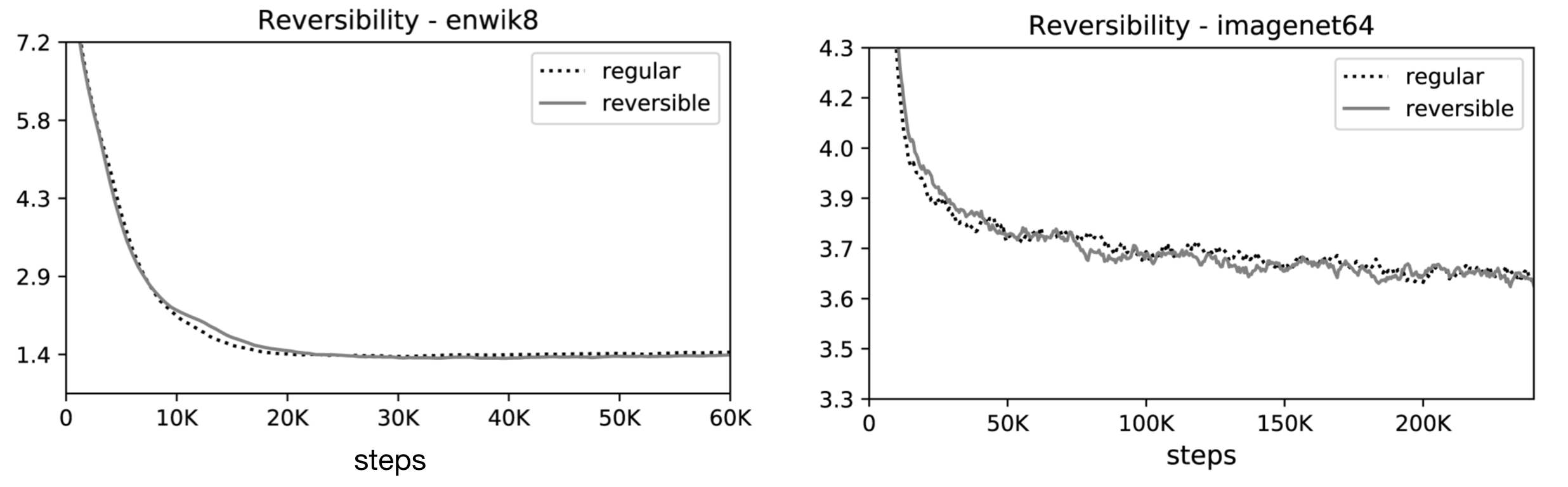
Comme l’attention LSH est une approximation de l’attention totale, sa précision s’améliore à mesure que la valeur du hachage augmente. Lorsque la valeur de hachage est de 8, l’attention LSH est presque équivalente à l’attention complète (celle du transformer).

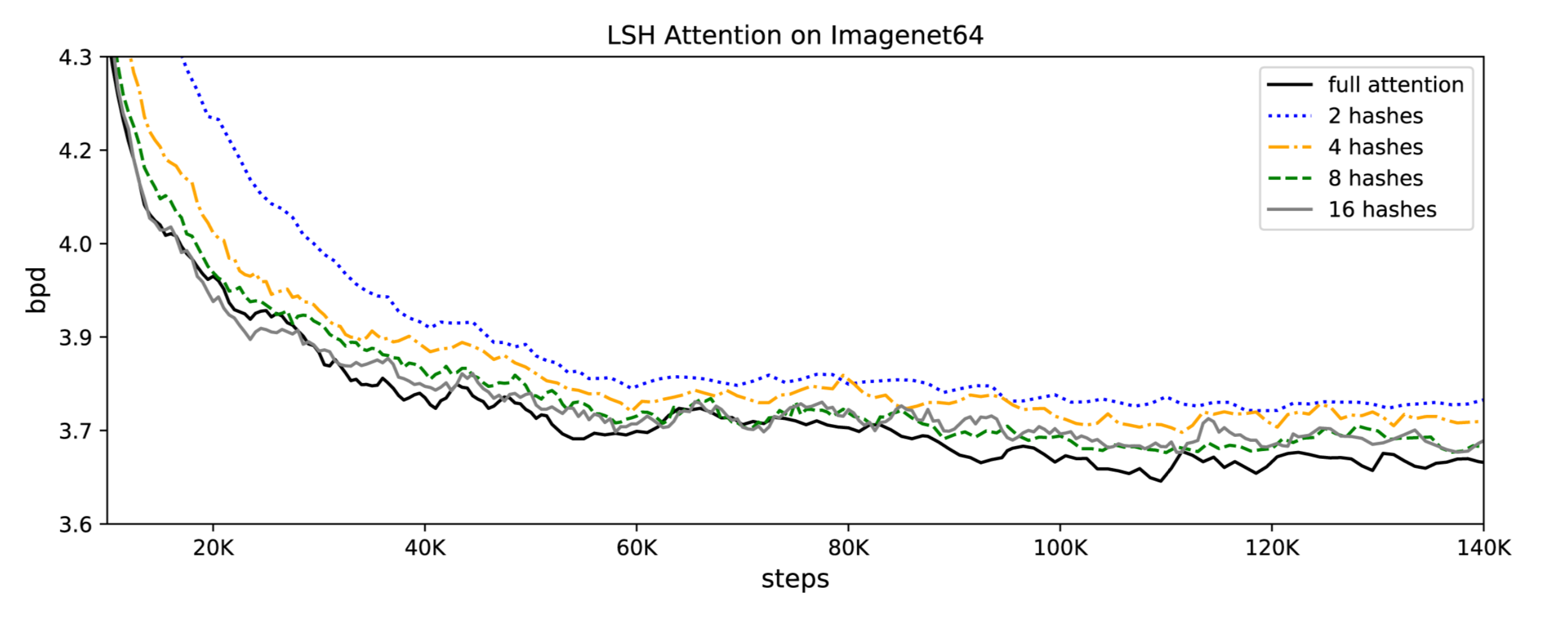
Ils ont également démontré que l’attention du transformer ralentit à mesure que la longueur de la séquence augmente, tandis que la vitesse d’attention LSH reste constante, et qu’elle fonctionne sur des séquences de longueur ~100K à la vitesse habituelle sur des GPUs de 8GB :


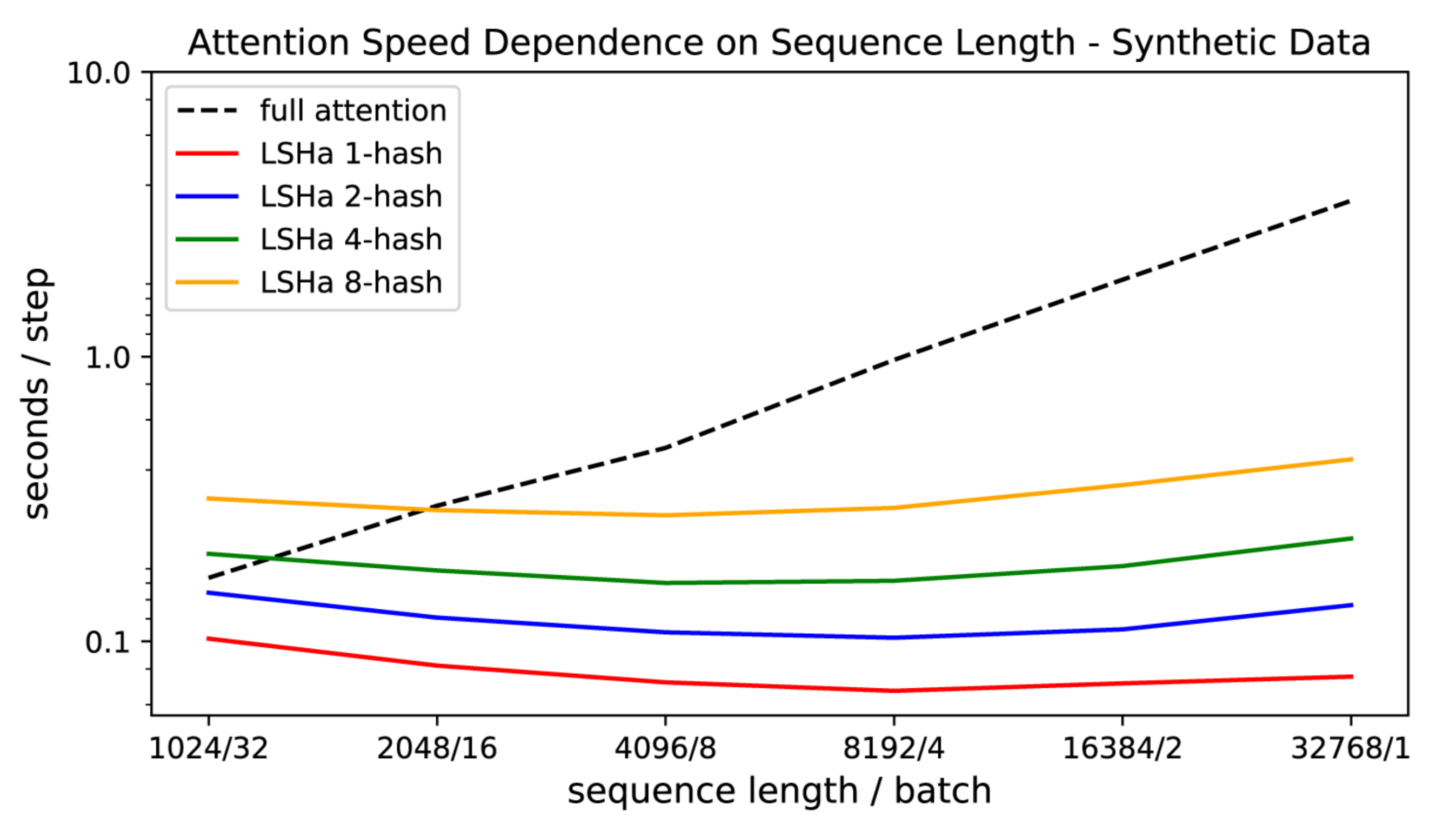
Le modèle final du reformer a donc des performances similaires à celles du modèle transformer, mais a montré une plus grande efficacité de stockage et une vitesse plus rapide sur les longues séquences.


Conclusion

Le code du reformer a été publié dans le cadre de la nouvelle bibliothèque Trax. Trax est une bibliothèque qui vise à vous permettre de comprendre l’apprentissage profond à partir de zéro. Le code du reformer comprend plusieurs exemples de tâches tel que de la génération d’images et de texte.


Références

Citation

@inproceedings{reformer_blog_post,
author = {Loïck BOURDOIS},
title = {Illustration du Reformer},
year = {2023},
url = {https://lbourdois.github.io/blog/nlp/Reformer/}
}

Vous pourriez aimer aussi