Avant-propos

Cet article est une traduction de celui de Maarten Grootendorst : A Visual Guide to Reasoning LLMs.
Maarten est co-auteur du livre Hands-On Large Language Models.


Introduction

DeepSeek-R1, OpenAI o3-mini et Google Gemini 2.0 Flash Thinking sont de parfaits exemples de la manière dont les LLM peuvent être poussés vers de nouveaux niveaux grâce à des cadres de « raisonnement ». Ils sont un marqueur du changement de paradigme consistant à passer à l’échelle les calculs de lors de la phase d’inférence plutôt que lors de la phase d’entraînement. Dans cet article, nous allons explorer le domaine des LLM avec raisonnement à travers plus de 50 illustrations. Nous nous intéresserons également aux calculs lors de la phase d’inférence, ainsi qu’au modèle DeepSeek-R1. Nous explorons ces concepts un par un pour développer une intuition sur ce changement de paradigme.


Qu’est-ce qu’un LLM avec raisonnement ?

Par rapport aux LLM classiques, les LLM avec raisonnement ont tendance à décomposer un problème en étapes plus petites (souvent appelées étapes de raisonnement ou processus de pensée) avant de répondre à une question donnée.

Que signifie un « processus de pensée », une « étape de raisonnement » ou une « chaîne de pensée » ? Bien que nous puissions philosopher sur la question de savoir si les LLM sont réellement capables de penser comme des humains, ces étapes de raisonnement décomposent le processus en inférences plus petites et structurées.

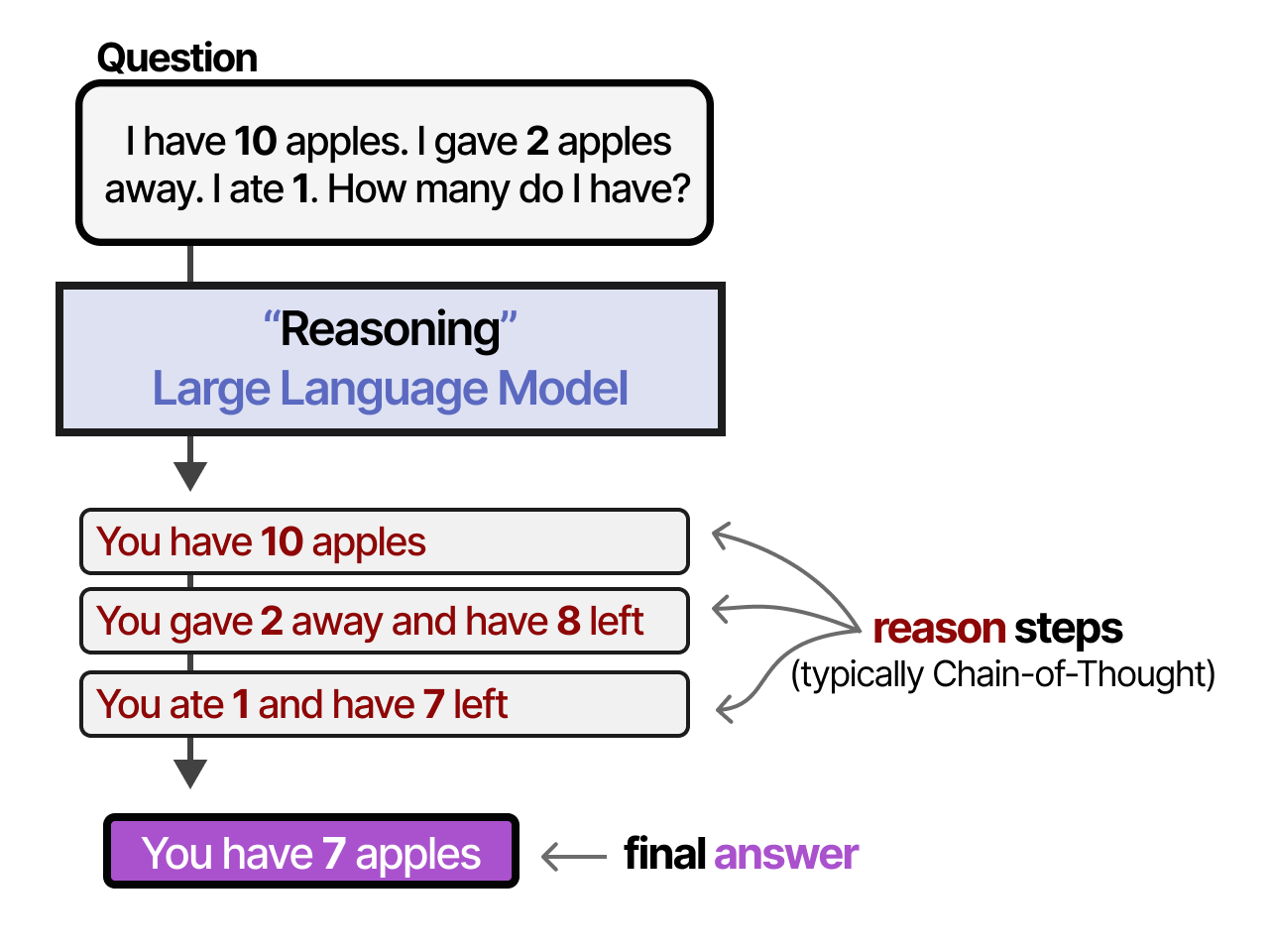
En d’autres termes, au lieu d’apprendre « quoi » répondre, les LLM apprennent « comment » répondre ! Pour comprendre comment les LLM avec raisonnement sont créés, commençons par explorer le changement de paradigme consistant à passer à l’échelle les calculs de lors de la phase d’inférence plutôt que lors de la phase d’entraînement.


Calculs à la phase d’entraînement

Jusqu’à mi-2024, pour augmenter la performance des LLM pendant le pré-entraînement, les développeurs augmentaient souvent la taille :
• du modèle (le nombre de paramètres)
• du jeu de données (le nombre de tokens montrés au modèle)
• de la puissance de calcul (le nombre de FLOPs i.e. le nombre d’opérations à virgule flottantes exécutables par seconde par notre GPU)
L’ensemble s’appelle le calcul à la phase d’entraînement, ce qui renvoie à l’idée que les données de pré-entraînement sont le « carburant de l’intelligence artificielle ». En substance, plus votre budget de pré-entraînement est important, plus le modèle obtenu sera performant.

Le calcul à la phase d’entraînement peut inclure à la fois le calcul nécessaire pendant l’entraînement et pendant le finetuning.

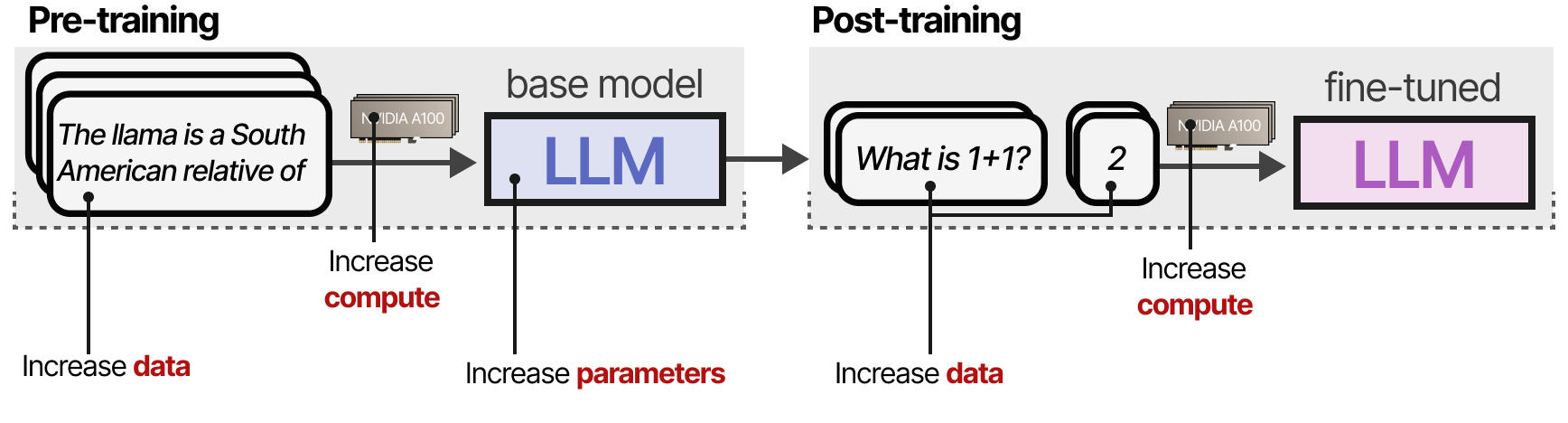
Le tout a été au cœur de l’amélioration des performances des LLM.

Lois d’échelle

La corrélation entre l’échelle d’un modèle (calcul, taille du jeu de données et taille du modèle) et ses performances est étudiée à l’aide de diverses lois d’échelle. Il s’agit de ce que l’on appelle des « lois de puissance », où l’augmentation d’une variable (par exemple, le calcul) entraîne un changement proportionnel d’une autre variable (par exemple, la performance).

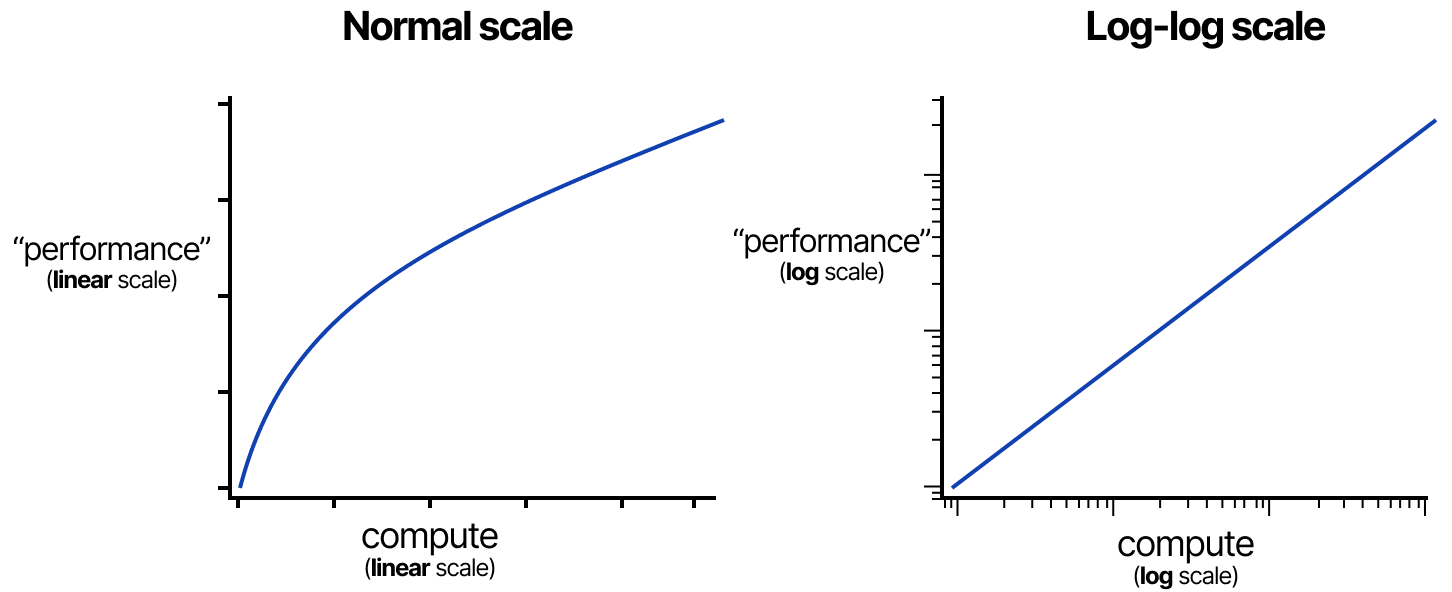
Elles sont généralement représentées sur une échelle logarithmique (donnant une ligne droite) afin de mettre en évidence la forte augmentation de la capacité de calcul. Les lois les plus connues sont celles de KAPLAN, MCCANDLISH et al. (2020) et de Chinchilla de DeepMind (notamment HOFFMANN, BORGEAUD, MENSCH et SIFRE) (2022). Ces lois indiquent plus ou moins que les performances d’un modèle augmentent avec l’accroissement de la puissance de calcul, du nombre de tokens et de celui des paramètres.

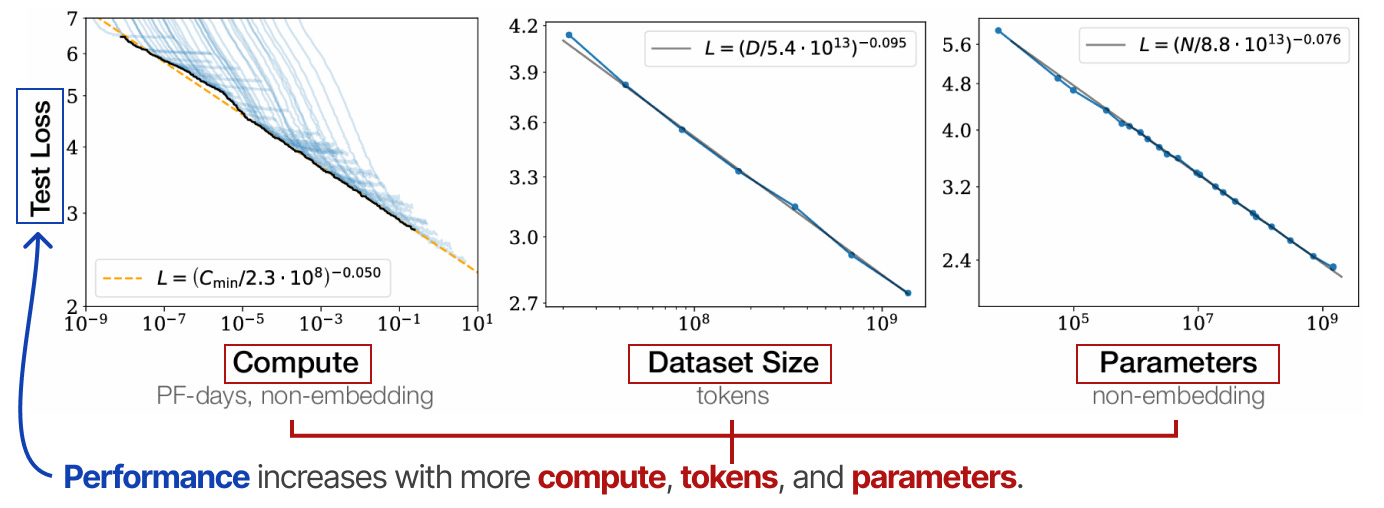
Figure annotée du papier de Kaplan & McCandlish montrant comment les performances peuvent augmenter avec différentes mesures de calcul (entraînement plus long, taille du jeu de données et nombre de paramètres).

Elles suggèrent que ces trois facteurs doivent être augmentés en tandem pour obtenir des performances optimales. La loi d’échelle de KAPLAN & MCCANDLISH stipule, qu’à calcul fixe, la mise à l’échelle de la taille du modèle est généralement plus efficace que la mise à l’échelle des données. En revanche, celle de Chinchilla suggère que la taille du modèle et les données sont d’égale importance. Cependant, tout au long de l’année 2024, alors que la puissance de calculs, la taille des jeux de données et le nombre de paramètres ont régulièrement augmenté, les gains de performance se sont avérés produire des rendements marginaux décroissants. C’est-à-dire que les rendements diminuent au fur et à mesure que l’on passe à l’échelle.

D’où la question suivante : « avons-nous atteint un mur ? »


Calculs à la phase d’inférence

L’aspect onéreux de l’augmentation des calculs de la phase d’entraînement a suscité un intérêt pour une autre solution, à savoir les calculs à la phase d’inférence. C’est-à-dire qu’au lieu d’augmenter continuellement les budgets du pré-entraînement, les calculs à la phase de test permettent aux modèles de « réfléchir plus longtemps » pendant l’inférence.

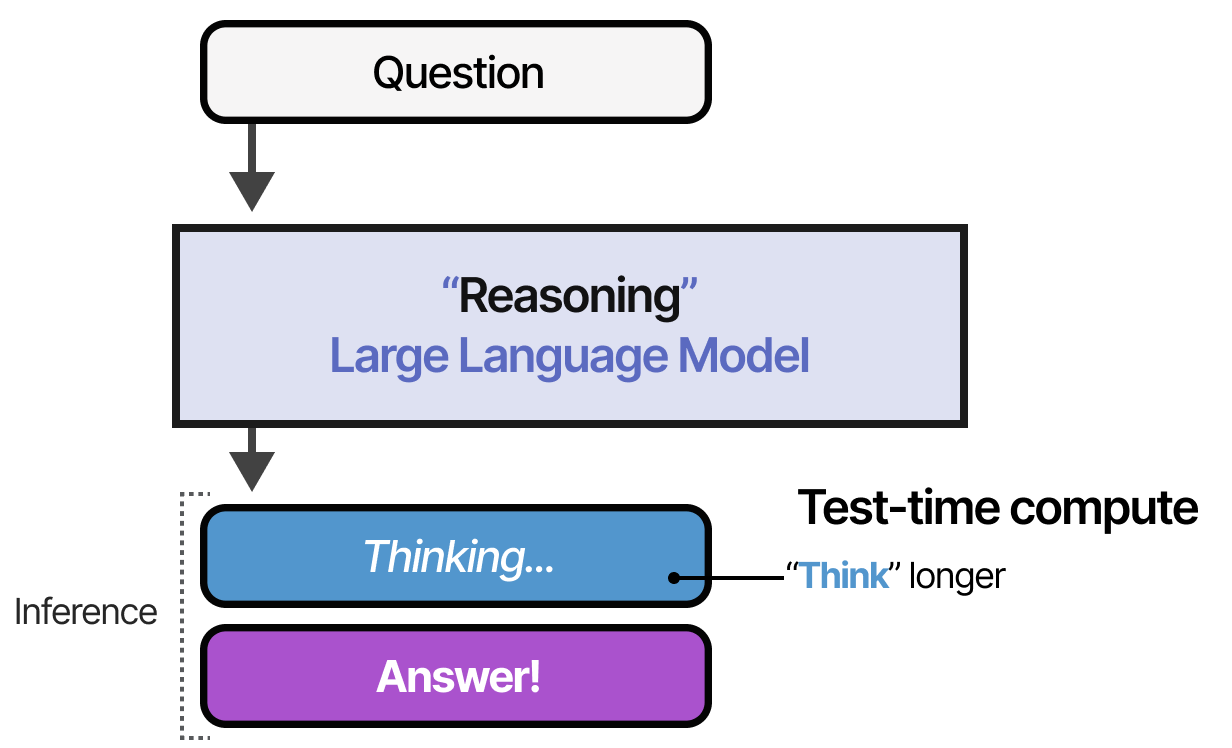
Les modèles sans raisonnement ne produisent que la réponse et sautent toute étape de « raisonnement » :

Les modèles de raisonnement, quant à eux, utilisent davantage de tokens pour aboutir à leur réponse par le biais d’un processus de « réflexion » systématique :

L’idée est que notre LLM doit dépenser plus de calculs (en VRAM) pour créer une réponse. Cependant, si tout le calcul est utilisé pour générer la réponse, c’est un peu inefficace. Au lieu de cela, en créant à l’avance davantage de tokens contenant des informations supplémentaires, des relations et de nouvelles réflexions, le modèle a consacré plus de temps à la génération de la réponse finale.



Lois d’échelle

Par rapport à la phase d’entraînement, les lois de mise à l’échelle pour la phase d’inférence sont relativement nouvelles. Il convient de noter deux sources intéressantes qui établissent un lien entre les deux phases. Tout d’abord, un article d’OpenAI montre que les calculs pour la phase d’inférence pourraient en fait suivre la même tendance que ceux de la phase d’entraînement.

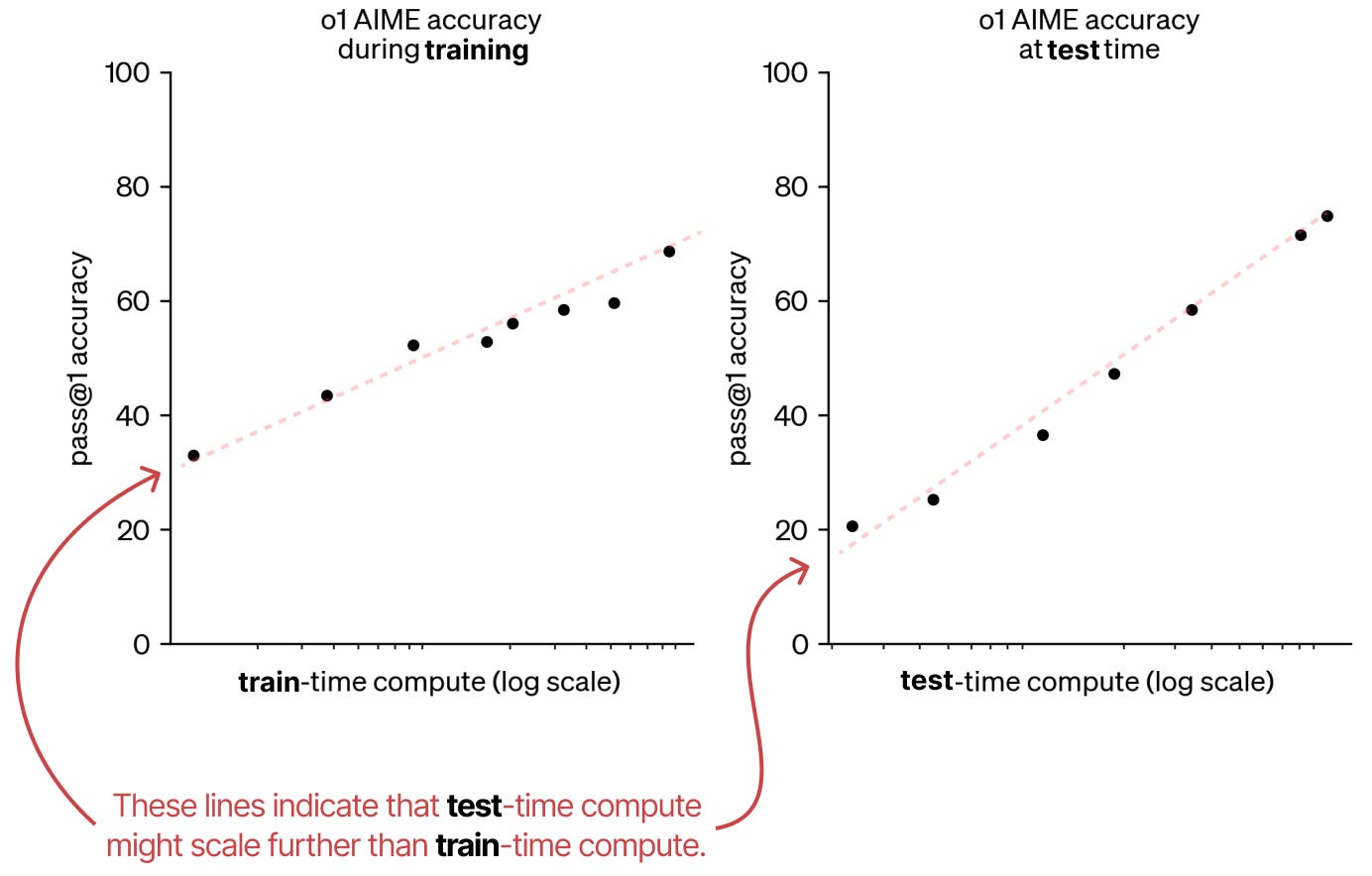
Figure annotée de l’article d’OpenAI.

Ainsi, ils affirment qu’il pourrait y avoir un changement de paradigme avec une focalisation sur la phase d’inférence bien qu’il s’agit encore d’un nouveau domaine. Deuxièmement, un article intéressant intitulé Scaling Scaling Laws with Board Games par JONES (2021), entraîne plusieurs AlphaZero de SILVER, HUBERT, SCHRITTWIESER et al. (2017) à jouer à Hex sur différents degrés de calcul.

L’auteur montre que les calculs à l’étape d’entraînement et d’inférence sont étroitement liés. Chaque ligne en pointillé indique le calcul minimum nécessaire pour un score ELO particulier.

Les calculs à l’étape d’inférence passant à l’échelle comme ceux de l’étape d’entraînement, on assiste à un changement de paradigme vers des modèles avec « raisonnement » utilisant davantage de calcul à l’inférence. Grâce à ce changement de paradigme, ces types de modèles ont une balance plus équilibrée entre entraînement (pré-entraînement et finetuning) et inférence.

La partie inférence passant à l’échelle également dans la durée :

Nous explorerons ce point plus en détails lorsque nous nous plongerons sur le DeepSeek-R1 !

Les différentes catégories de calculs à l’inférence

L’incroyable succès des modèles avec raisonnement tels que DeepSeek R-1 et OpenAI o1 montre qu’il existe d’autres techniques que la simple pensée « plus longue ». Comme nous le verrons, les calculs à l’inférence peuvent prendre différentes formes, notamment la chaîne de pensée, la révision de réponses, le retour en arrière, l’échantillonnage et bien d’autres choses. D’après SNELL et al. (2024), on peut les classer en deux grandes catégories :
• La vérification des recherches (échantillonnage des générations et sélection de la meilleure réponse)
• La modification de la distribution de la proposition (processus de « réflexion » entraîné)

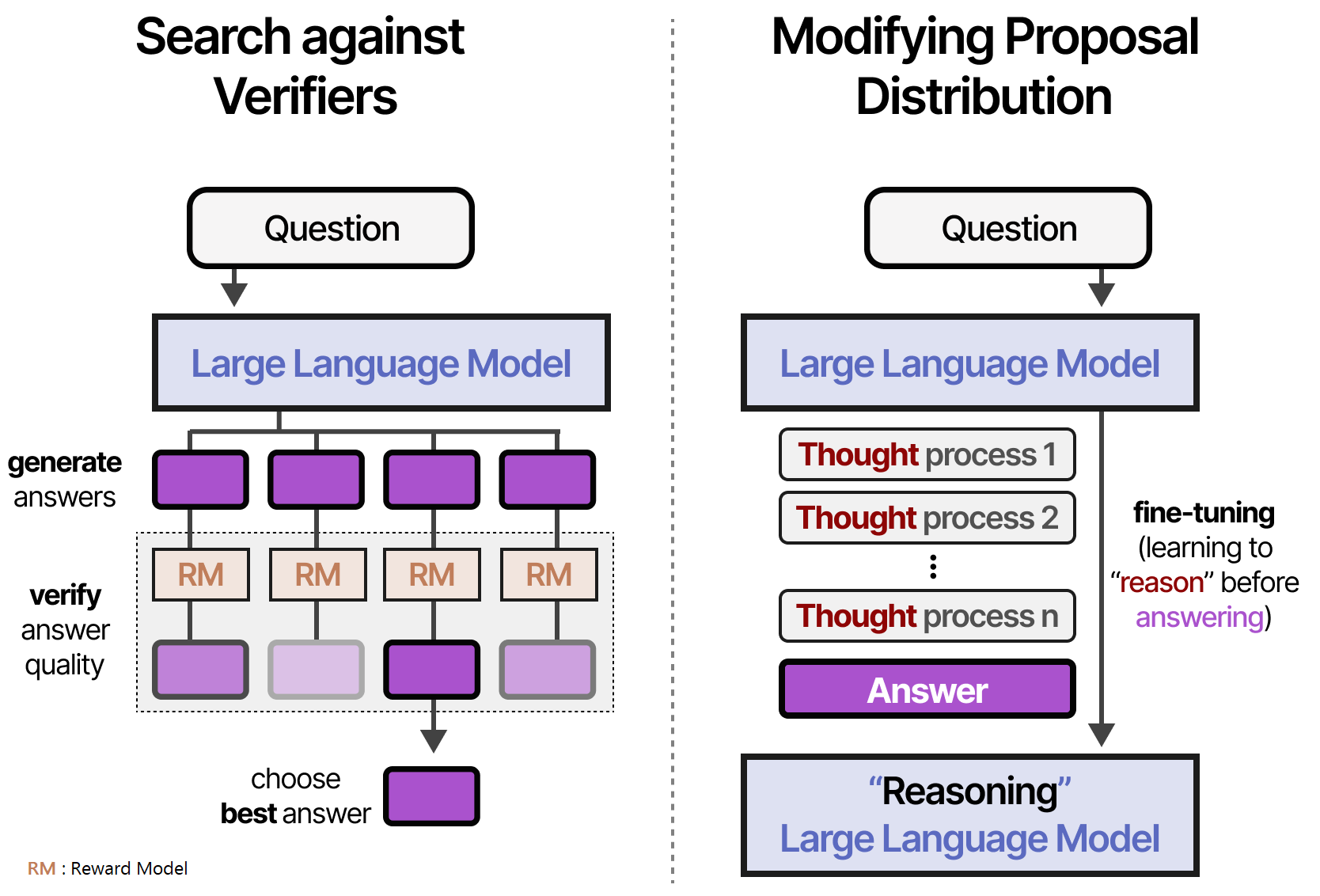
Ainsi, la vérification des recherches est axée sur la sortie, tandis que la modification de la distribution de la proposition est axée sur l’entrée.

Il y a deux types de vérificateurs que nous allons étudier :
• Les Modèles de récompense des résultats (ORM pour Outcome Reward Models)
• Les Modèles de récompense des processus (PRM pour Process Reward Models)
Les ORM ne jugent que le résultat et ne se préoccupe pas du processus sous-jacent :

A contratio les PRM jugent également le processus qui conduit au résultat (le « raisonnement ») :

Un exemple concret pour rendre ces étapes de raisonnement un peu plus explicites :

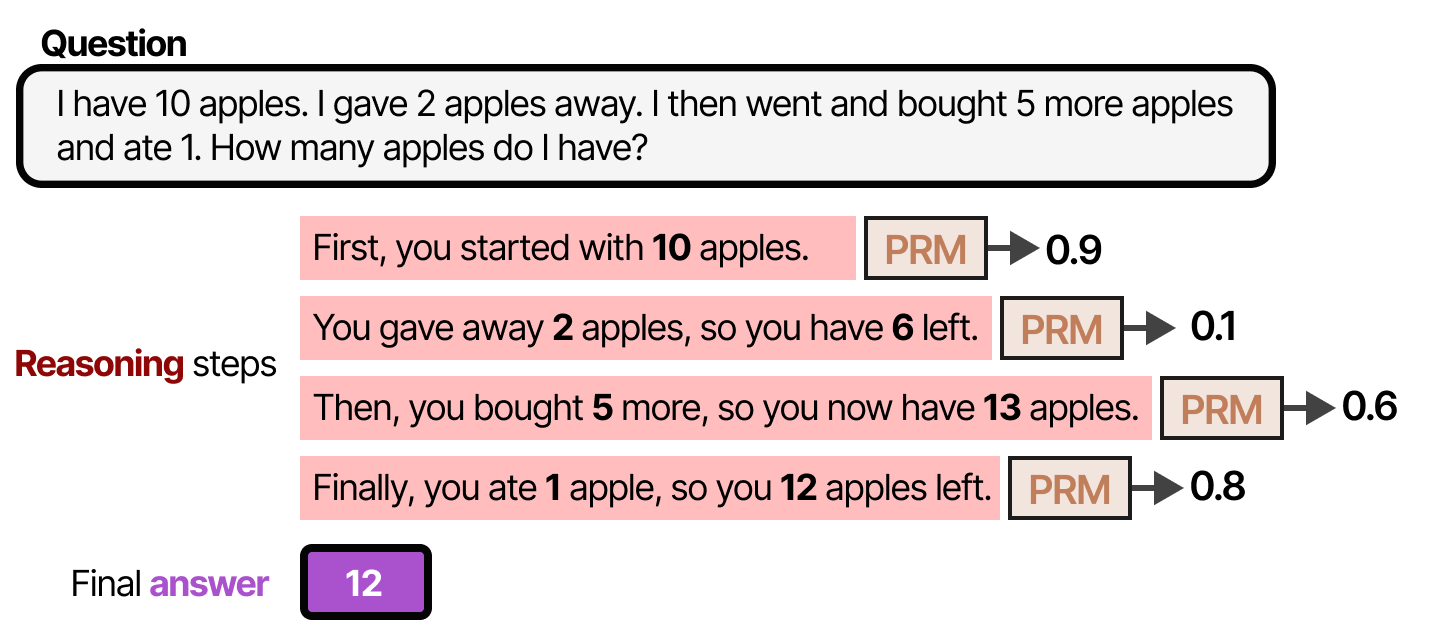
Notez que l’étape 2 est une étape de raisonnement médiocre et qu’elle est mal notée par le PRM. Maintenant que vous avez une vue générale de la différence entre ORM et PRM, voyons comment ils peuvent être appliqués dans différentes techniques de vérification !


La vérification des recherches

La vérification des recherches implique généralement deux étapes :
• Premièrement, plusieurs échantillons de raisonnement et de réponses sont créés
• Deuxièmement, un vérificateur (modèle de récompense) évalue la sortie générée

Le vérificateur est généralement un LLM, finetuné à juger le résultat (ORM) ou le processus (PRM). L’un des principaux avantages de l’utilisation de vérificateurs est qu’il n’est pas nécessaire de réentraîner ou de finetuner le LLM que vous utilisez pour répondre à la question.

Vote à la majorité

La méthode la plus simple consiste à ne pas utiliser de modèle de récompense ou de vérificateur, mais à procéder à un vote à la majorité. Nous laissons le modèle générer plusieurs réponses et la réponse la plus fréquente sera la réponse finale.

Cette méthode est également appelée autoconsistance par WANG et al. (2022) afin de souligner la nécessité de générer plusieurs réponses et étapes de raisonnement.

Meilleur échantillon parmi N

La méthode Meilleur échantillon parmi \(N\) (Best-of-\(N\) samples) génère \(N\) échantillons et utilise ensuite un vérificateur (ORM) pour évaluer chaque réponse :

  • Tout d’abord, le LLM (souvent appelé l’Offrant) génère plusieurs réponses en utilisant une température élevée ou variable.
  • Ensuite, chaque réponse est soumise à un ORM qui en note la qualité. La réponse qui obtient le score le plus élevé est sélectionnée :

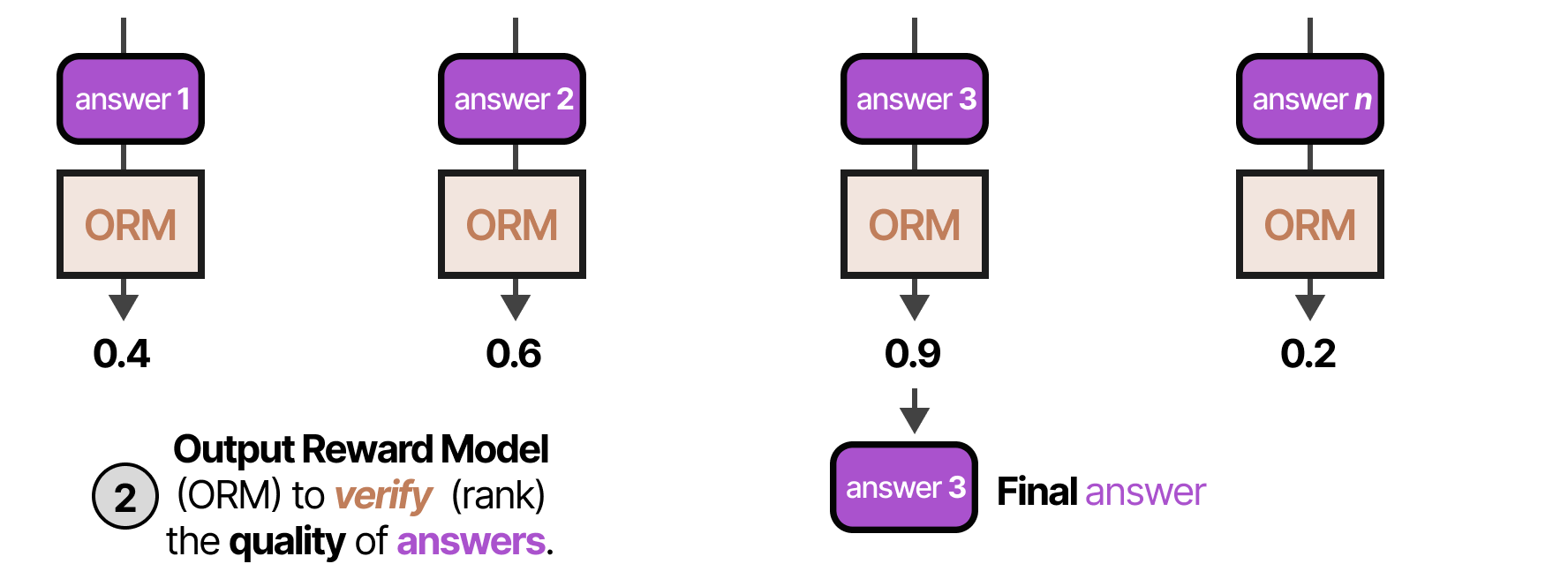
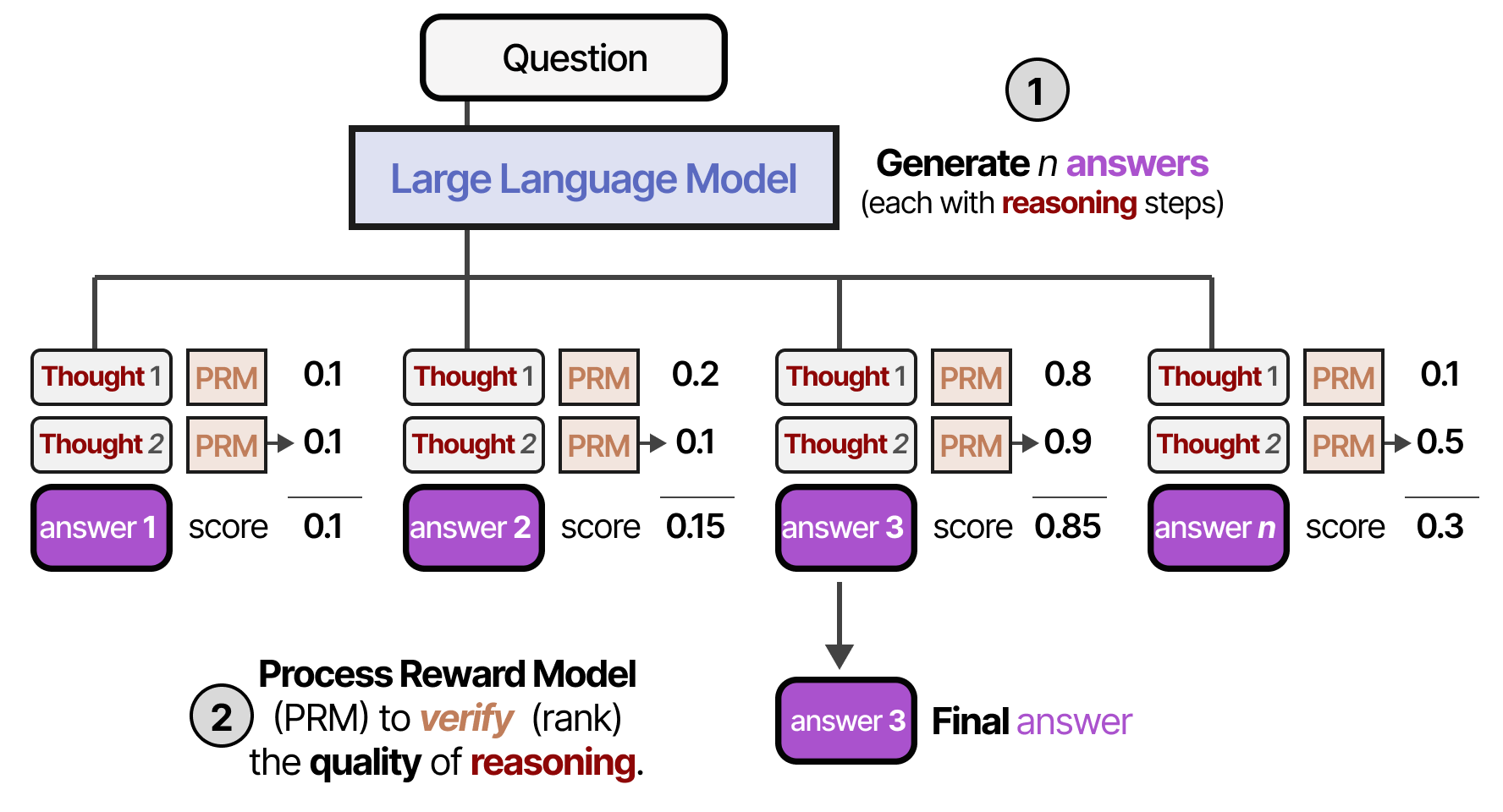
Au lieu de juger la réponse, on peut également juger le processus de raisonnement à l’aide d’un PRM qui évalue la qualité de chaque étape du raisonnement. Il choisit au final le candidat ayant la moyenne totale la plus élevée.

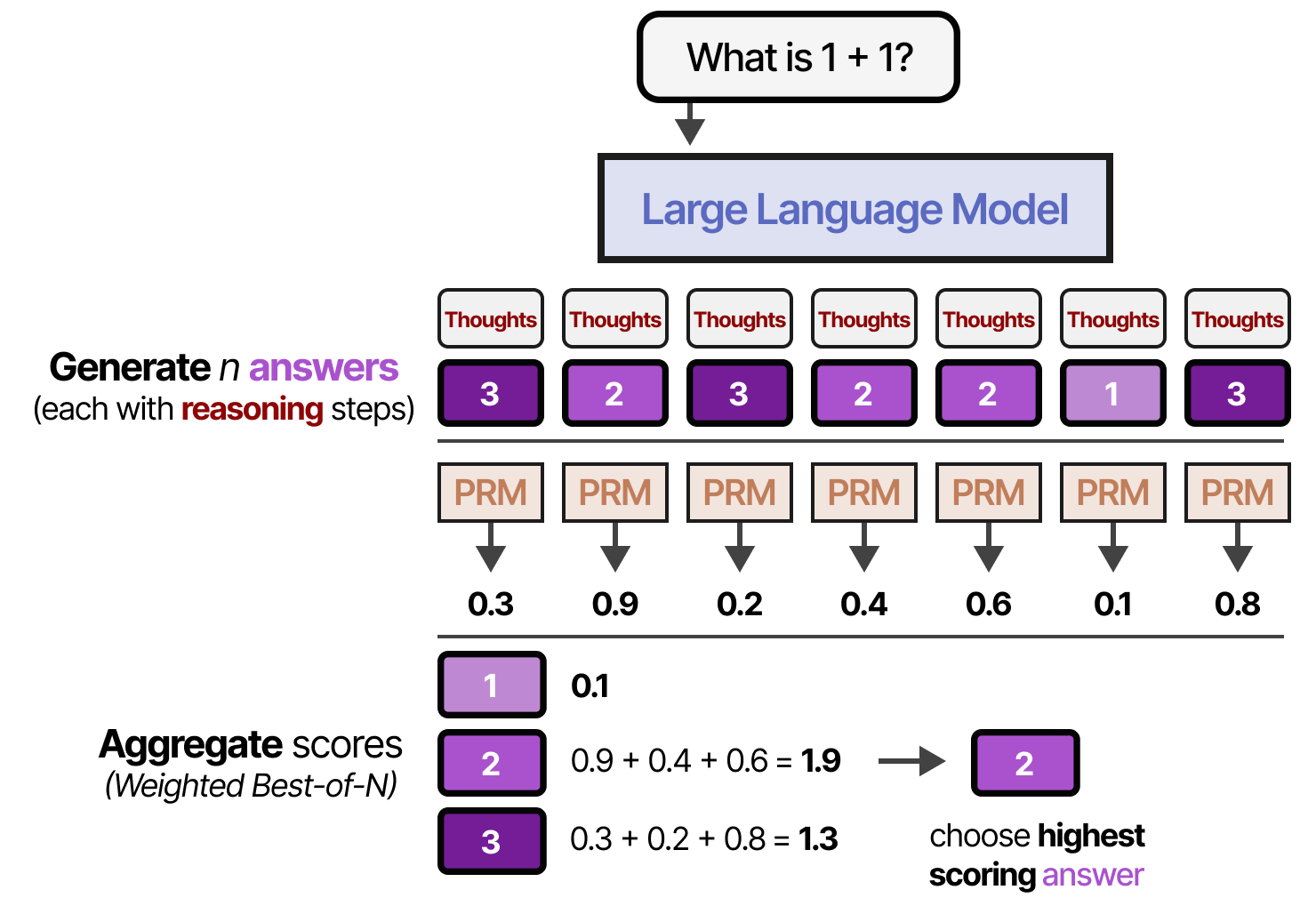
Avec les deux types de vérifications, nous pouvons également pondérer chaque réponse candidate et choisir celle qui a le poids total le plus élevé. C’est ce qu’on appelle les échantillons Best-of-\(N\) pondérés :



Recherche en faisceau avec PRM

Ce processus de génération de réponses et d’étapes intermédiaires peut être étendu avec la recherche en faisceau. Avec la recherche en faisceau, plusieurs étapes de raisonnement sont échantillonnées et chacune d’entre elles est évaluée par le PRM (comme pour l’arbre de pensée de YAO et al. (2023)). Les top-3 des faisceaux (chemins les mieux notés) sont suivis tout au long du processus.

Cette méthode permet d’arrêter rapidement les chemins de « raisonnement » ne s’avèrant pas fructueux (mal notés par le MRP). Les réponses obtenues sont ensuite pondérées à l’aide de l’approche Best-of-\(N\) que nous avons explorée précédemment.

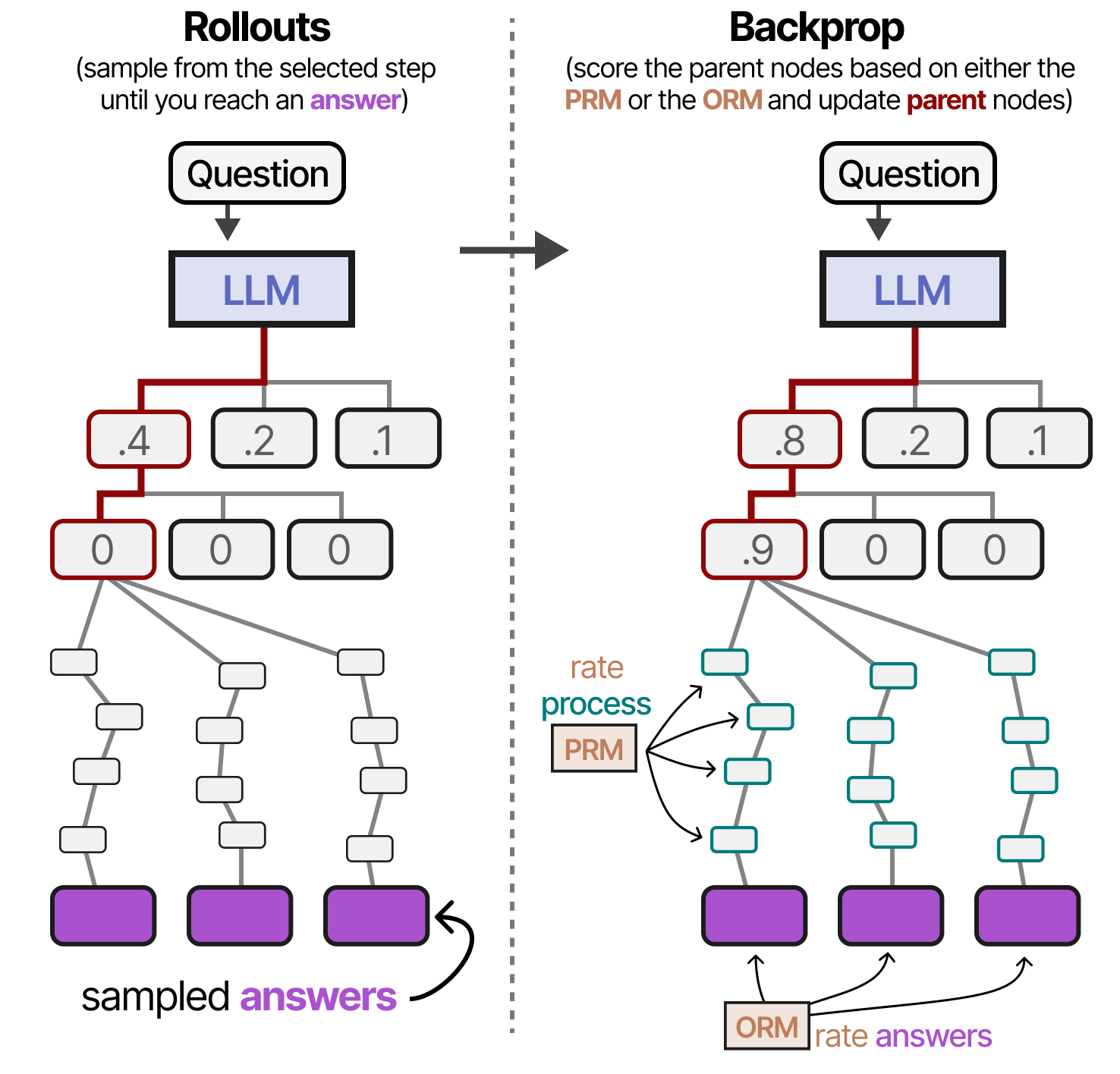
Recherche arborescente de Monte Carlo

La recherche arborescente de Monte Carlo est une excellente technique pour rendre les recherches arborescentes plus efficaces. Elle se compose de quatre étapes :
• Sélection (sélectionner une feuille donnée sur la base d’une formule prédéterminée)
• Expansion (créer des nœuds supplémentaires)
• Simulation (création aléatoire de nouveaux nœuds jusqu’à ce que vous atteigniez la fin)
• Rétropropagation (mise à jour des scores des nœuds parents sur la base des résultats)
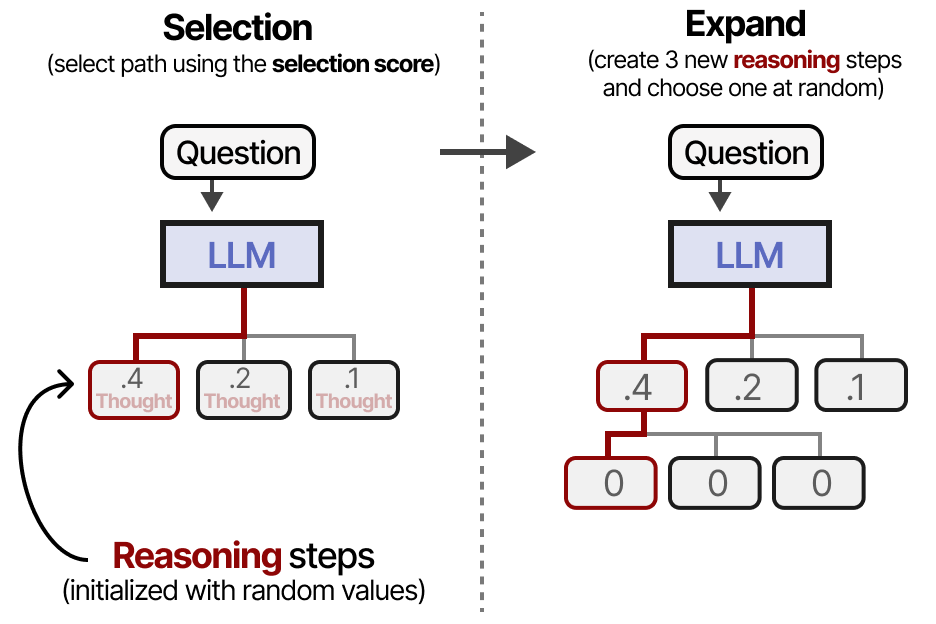
L’objectif principal de ces étapes est de continuer à développer les meilleures étapes de raisonnement tout en explorant d’autres voies. Il s’agit donc d’un équilibre entre l’exploration et l’exploitation. Voici un exemple de la manière dont les nœuds sont notés et sélectionnés :

Ainsi, lorsque nous sélectionnons une nouvelle étape de raisonnement à explorer, il n’est pas nécessaire qu’elle soit la plus performante jusqu’à présent. En utilisant ce type de formule, nous commençons par sélectionner un nœud (étape de raisonnement) et nous l’étendons en générant de nouvelles étapes de raisonnement. Comme précédemment, cela peut se faire avec des valeurs de température raisonnablement élevées et variables :

L’une des étapes du raisonnement élargi est sélectionnée et simulée plusieurs fois jusqu’à ce qu’elle aboutisse à plusieurs réponses. Ces simulations peuvent être jugées sur la base des étapes du raisonnement (PRM), des récompenses (ORM) ou d’une combinaison des deux. Les scores des nœuds parents sont mis à jour (rétropropagation) et nous pouvons recommencer le processus en commençant par la sélection.




Modifier la distribution des propositions

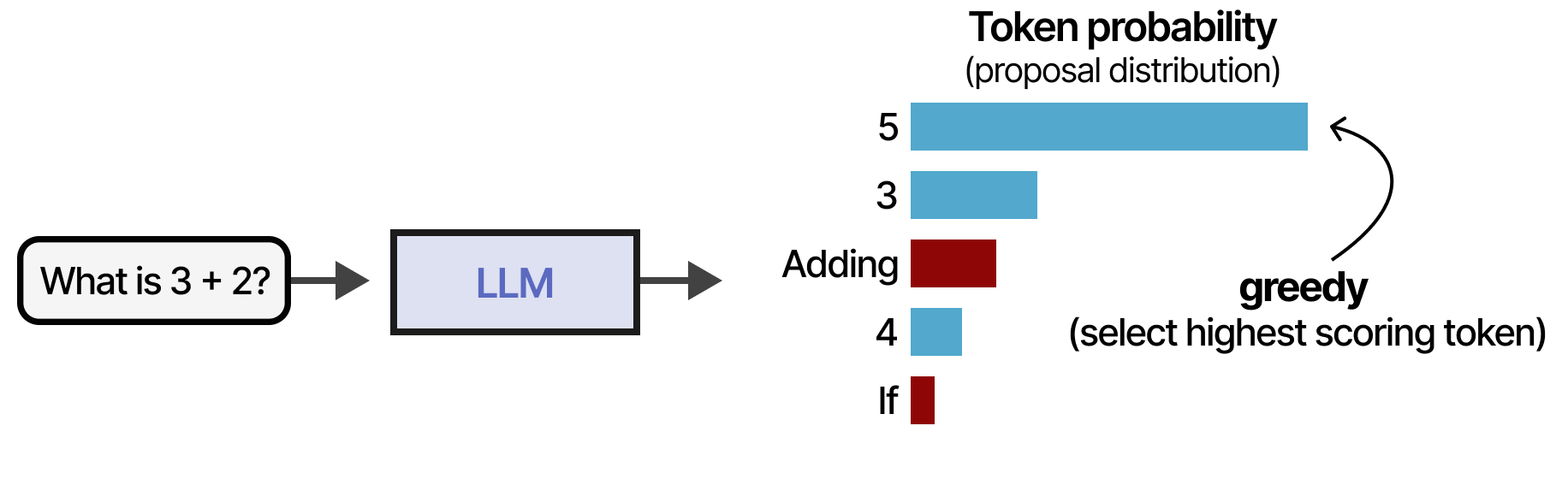
Voyons à présent la deuxième catégorie pour concevoir un LLM avec raisonnement. Au lieu de rechercher les étapes de raisonnement correctes avec des vérificateurs (axé sur les sorties), le modèle est entraîné à créer des étapes de raisonnement améliorées (axé sur les entrées). En d’autres termes, la distribution à partir de laquelle les complétions/pensées/tokens sont échantillonnés est modifiée. Imaginons que nous disposions d’une question et d’une distribution à partir desquelles nous pouvons prélever des tokens. Une stratégie courante consisterait à obtenir le token ayant obtenu le score le plus élevé :

Notez toutefois que certains des tokens sont colorés en rouge dans l’image ci-dessus. Ce sont les tokens qui sont les plus susceptibles de conduire à un processus de raisonnement :

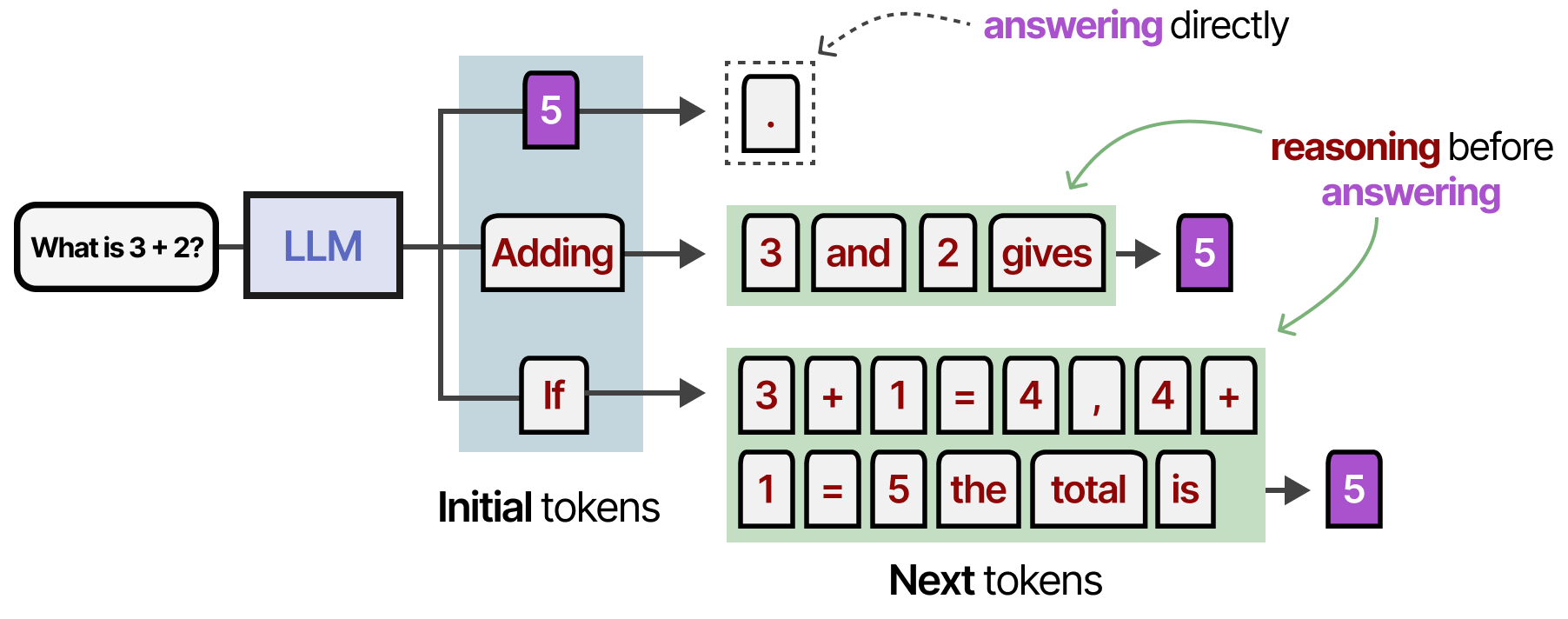
Bien qu’il ne soit pas nécessairement erroné de choisir le token le plus vraisemblable, la sélection d’un token conduisant à un processus de raisonnement tend à améliorer la réponse. Lorsque nous modifions la distribution des propositions (i.e. la distribution de probabilité des tokens), nous faisons en sorte que le modèle reclasse la distribution de manière à ce que les tokens de raisonnement soient sélectionnés plus fréquemment :

Il existe plusieurs méthodes pour modifier la distribution pouvant être classées en deux grandes catégories :
• Modifier l’instruction (i.e. le prompt)
• Entraîner le modèle à se concentrer sur les tokens/processus de raisonnement

Modification du prompt

La modification du prompt est un procédé dont le but est d’améliorer les résultats. Il peut également inciter le modèle à présenter certains des processus de raisonnement que nous avons vus précédemment. Pour modifier la distribution, nous pouvons fournir au modèle des exemples (apprentissage en contexte) qu’il doit suivre pour générer un comportement de type raisonnement :

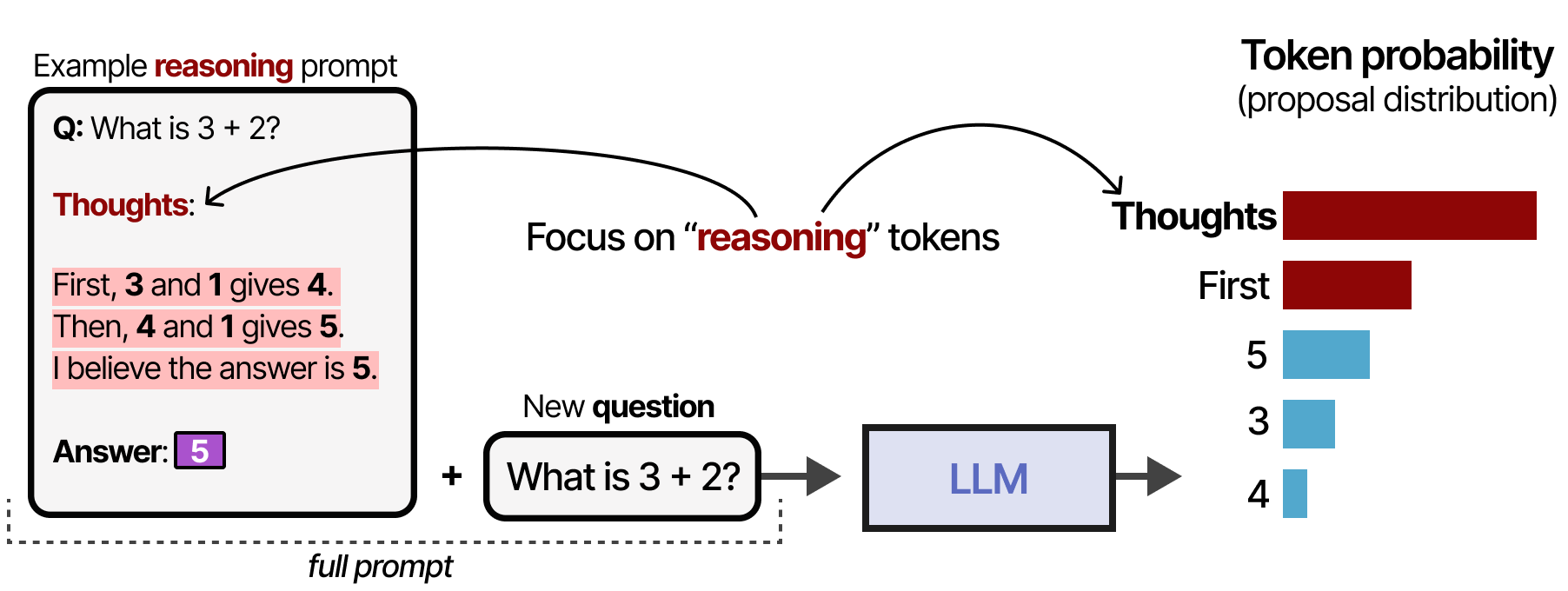
Ce processus peut être encore simplifié en déclarant simplement « Let’s think step-by-step » comme l’a montré KOJIMA et al. (2022). Cela modifie la répartition des propositions de telle sorte que le LLM a tendance à décomposer le processus avant de répondre :

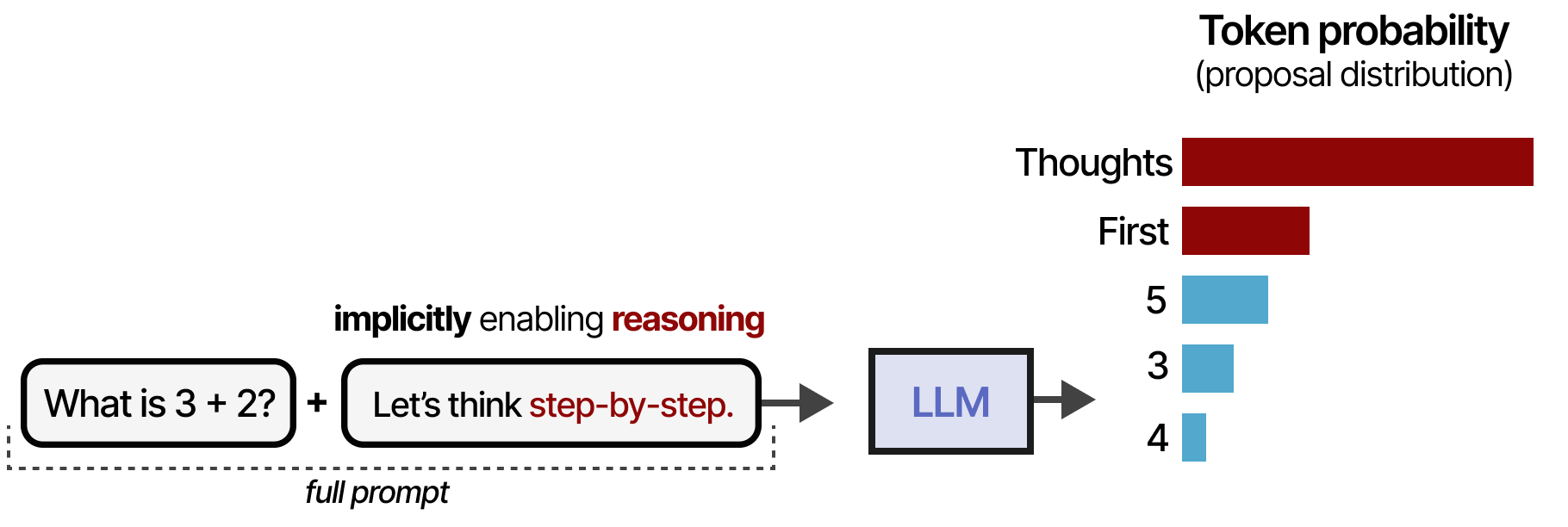
Cependant, le modèle n’a pas appris de manière intrinsèque à suivre ce processus. De plus, il s’agit d’un processus statique et linéaire qui empêche l’autorenouvellement. En effet, si un modèle commence par un processus de raisonnement incorrect, il a tendance à le conserver au lieu de le réviser.

STaR

Outre les prompts, nous pouvons faire en sorte que le modèle apprenne à « raisonner » en l’entraînant de manière à ce qu’il soit récompensé pour les étapes de raisonnement qu’il génère. Cela implique généralement un jeu de données de raisonnement et un apprentissage par renforcement pour récompenser certains comportements. Une technique fréquemment utilisés est STaR ou Self-Taught Reasoner par ZELIKMAN, WU et al. (2022). STaR est une méthode qui utilise le LLM pour générer ses propres données de raisonnement en tant qu’entrée pour finetuner le modèle. Dans la première étape (1), le LLM génère un duo d’étapes de raisonnement et une réponse. Si la réponse est correcte (2a), le raisonnement et la réponse sont ajoutés à un jeu de données d’entraînement sous la forme de triplet (3b). Ces données sont utilisées pour effectuer un finetuning supervisé du modèle (5) :

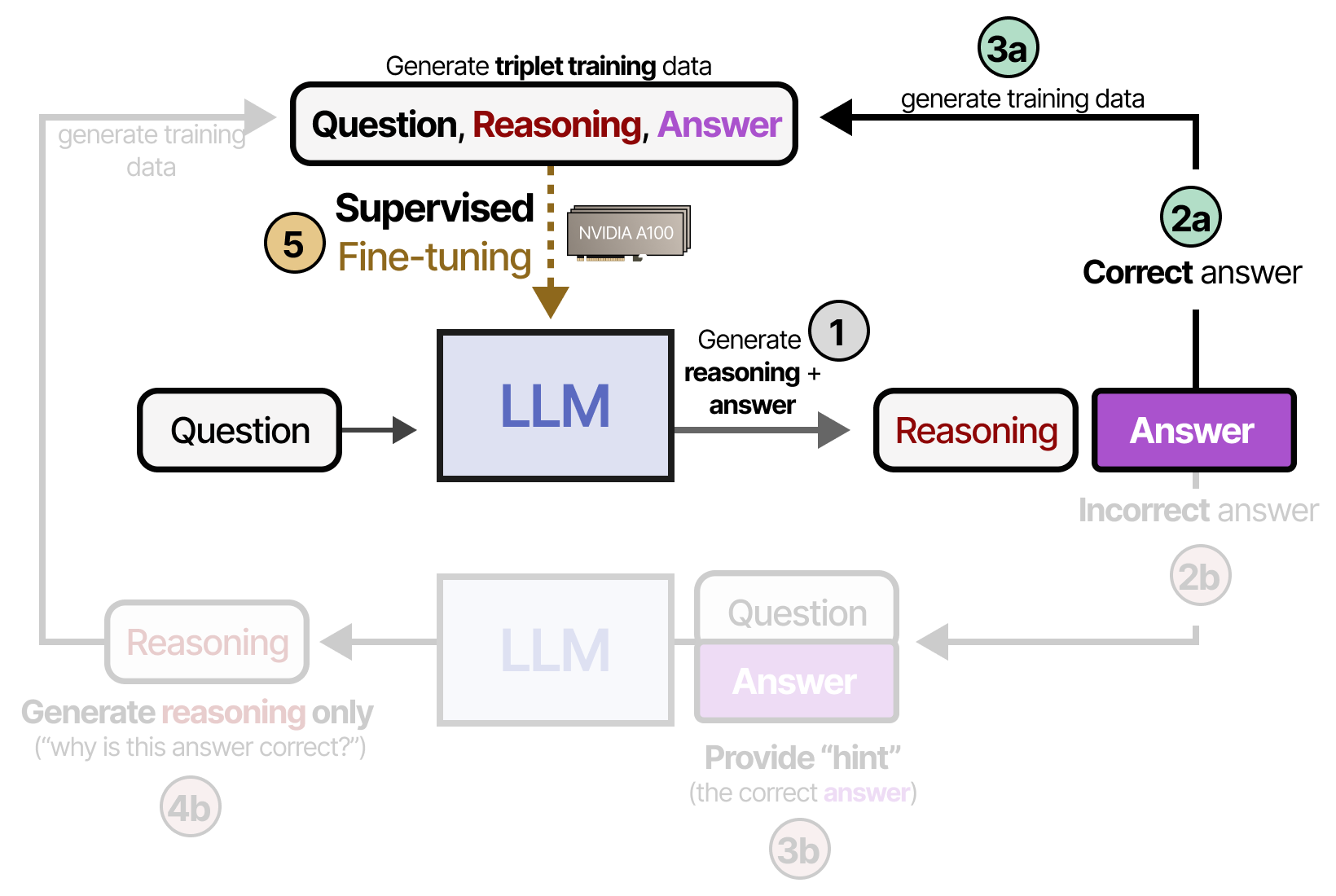
Si toutefois le modèle fournit une réponse incorrecte (2b), nous donnons un « indice » (i.e. la bonne réponse) et demandons au modèle d’expliquer pourquoi cette réponse est correcte (4b). L’étape finale consiste à ces données aux triplets d’entraînement pour effectuer un finetuning supervisé du modèle (5) :

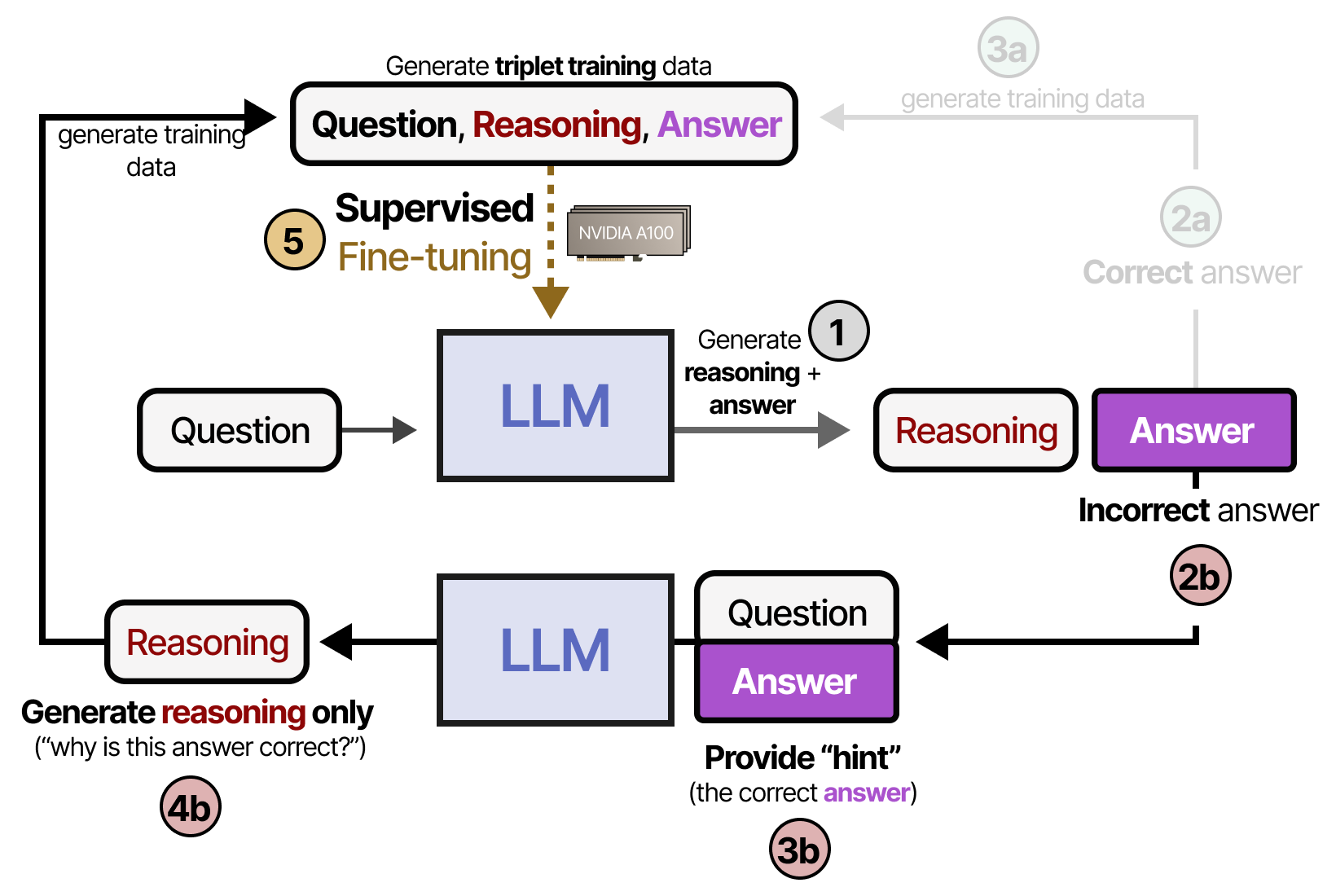
Un élément clé ici (ainsi que de nombreuses autres techniques de modification de la distribution) est que nous entraînons explicitement le modèle à suivre les processus de raisonnement que nous lui montrons. En d’autres termes, nous décidons de la manière dont le processus de raisonnement doit se dérouler par le biais d’un finetuning supervisé. Le pipeline complet est très intéressant car il génère essentiellement des exemples d’entraînement synthétiques. L’utilisation d’exemples d’entraînement synthétiques est une méthode incroyable pour distiller ce processus de raisonnement dans d’autres modèles.


DeepSeek-R1

Un modèle de raisonnement majeur est le DeepSeek-R1 (2025) de DeepSeek, dont les poids sont open-source. En concurrence directe avec le modèle de raisonnement OpenAI o1 d’OpenAI, DeepSeek-R1 a eu un impact majeur sur le domaine. DeepSeek a fait un travail remarquable en distillant élégamment le raisonnement dans son modèle de base (DeepSeek-V3-Base (2024)) par le biais de diverses techniques. Il est intéressant de noter qu’aucun vérificateur n’a été utilisé et qu’au lieu de recourir à un finetuning supervisé pour distiller le comportement de raisonnement, l’accent a été mis sur l’apprentissage par renforcement. Voyons comment l’équipe de DeepSeek a procédé !

Raisonner avec DeepSeek-R1 Zero

Le modèle expérimental appelé DeepSeek-R1 Zero a constitué une avancée majeure dans la l’élaboration de DeepSeek-R1. À partir de DeepSeek-V3-Base, au lieu d’utiliser un finetuning supervisé sur un jeu de données de raisonnement, ils ont seulement utilisé l’apprentissage par renforcement (RL) pour activer le comportement de raisonnement. Pour ce faire, ils commencent par un prompt très simple (similaire à un prompt système) à utiliser dans le pipeline :

Notez qu’ils mentionnent explicitement que le processus de raisonnement doit se dérouler entre les balises <think>, mais qu’ils ne précisent pas à quoi doit ressembler le processus de raisonnement. Lors de la phase d’apprentissage par renforcement, deux récompenses spécifiques basées sur des règles ont été créées :
• Récompenses pour la précision : Récompense la réponse en la testant.
• Récompenses pour le format : Récompense l’utilisation des balises <thinking> et <answer>.
L’algorithme d’apprentissage par renforcement utilisé dans ce processus est appelé le Group Relative Policy Optimization (GRPO) de SHAO, WANG, ZHU, GUO et al. (2024). L’intuition qui sous-tend cet algorithme est qu’il rend plus ou moins probables tous les choix qui ont conduit à une réponse correcte ou incorrecte. Ces choix peuvent être à la fois des ensembles de tokens et des étapes de raisonnement.

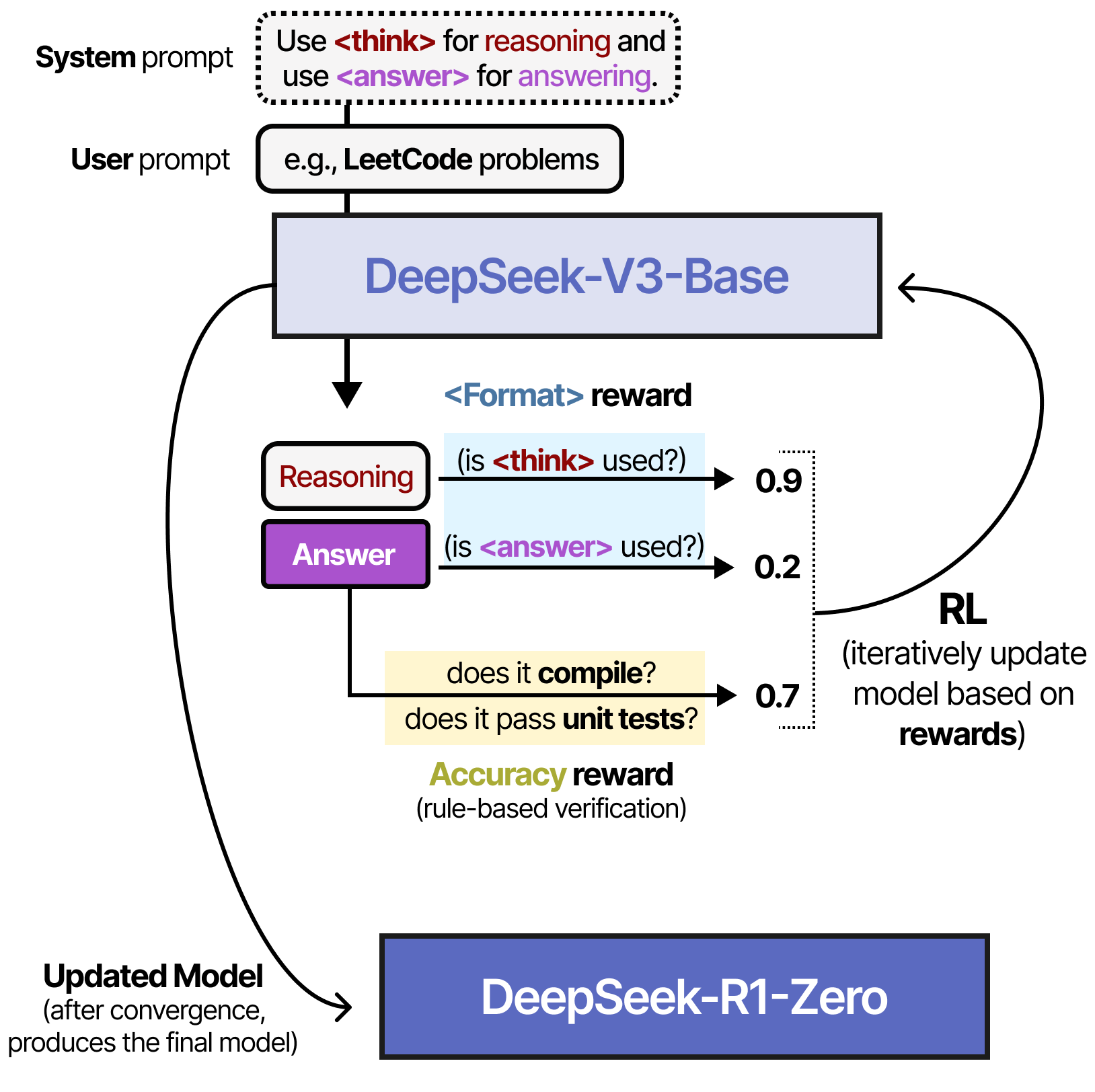
Il est intéressant de noter qu’aucun exemple n’a été donné sur la manière dont le processus <think> devrait se dérouler. Il est simplement indiqué qu’il faut utiliser les balises <think>, et rien de plus ! En fournissant ces récompenses indirectes liées au comportement de la chaîne de pensée, le modèle a appris par lui-même que plus le processus de raisonnement est long et complexe, plus la réponse a de chances d’être correcte.

En utilisant des récompenses indirectes, le modèle explore librement le comportement le plus optimal de type chaîne de pensée via des étapes de raisonnement de plus en plus nombreuses.

Ce graphique est particulièrement important car il renforce le changement de paradigme de la focalisation des calculs de l’entraînement vers l’inférence. Comme ces modèles génèrent des séquences de pensées plus longues, ils se concentrent sur le calcul d’inférence. En utilisant ce pipeline, les auteurs ont constaté que le modèle découvre de lui-même le comportement le plus optimal de type chaîne de pensée, y compris les capacités de raisonnement avancées telles que l’autoréflexion et l’auto-vérification. Cependant, le modèle présentait encore un inconvénient de taille. Il était peu lisible et avait tendance à mélanger les langues. Ils ont donc exploré une autre solution, qui a abouti au désormais célèbre DeepSeek-R1.

DeepSeek-R1

Voyons comment ils ont stabilisé le processus de raisonnement !
Pour créer DeepSeek-R1, les auteurs ont suivi cinq étapes :

  1. Démarrage à froid
  2. Apprentissage par renforcement axé sur le raisonnement
  3. Filtrage des données
  4. Finetuning supervisé
  5. Apprentissage par renforcement pour tous les scénarios

Dans l’étape 1, DeepSeek-V3-Base a été finetuné avec un petit jeu de données de raisonnement de haute qualité (≈ 5 000 tokens). Cela a été fait pour éviter le problème de démarrage à froid qui entraîne une mauvaise lisibilité.

À l’étape 2, le modèle résultant a été entraîné à l’aide d’un processus d’apprentissage par renforcement similaire à celui utilisé pour entraîner DeepSeek-R1-Zero. Cependant, une autre mesure de récompense a été ajoutée pour s’assurer que la langue cible reste cohérente.

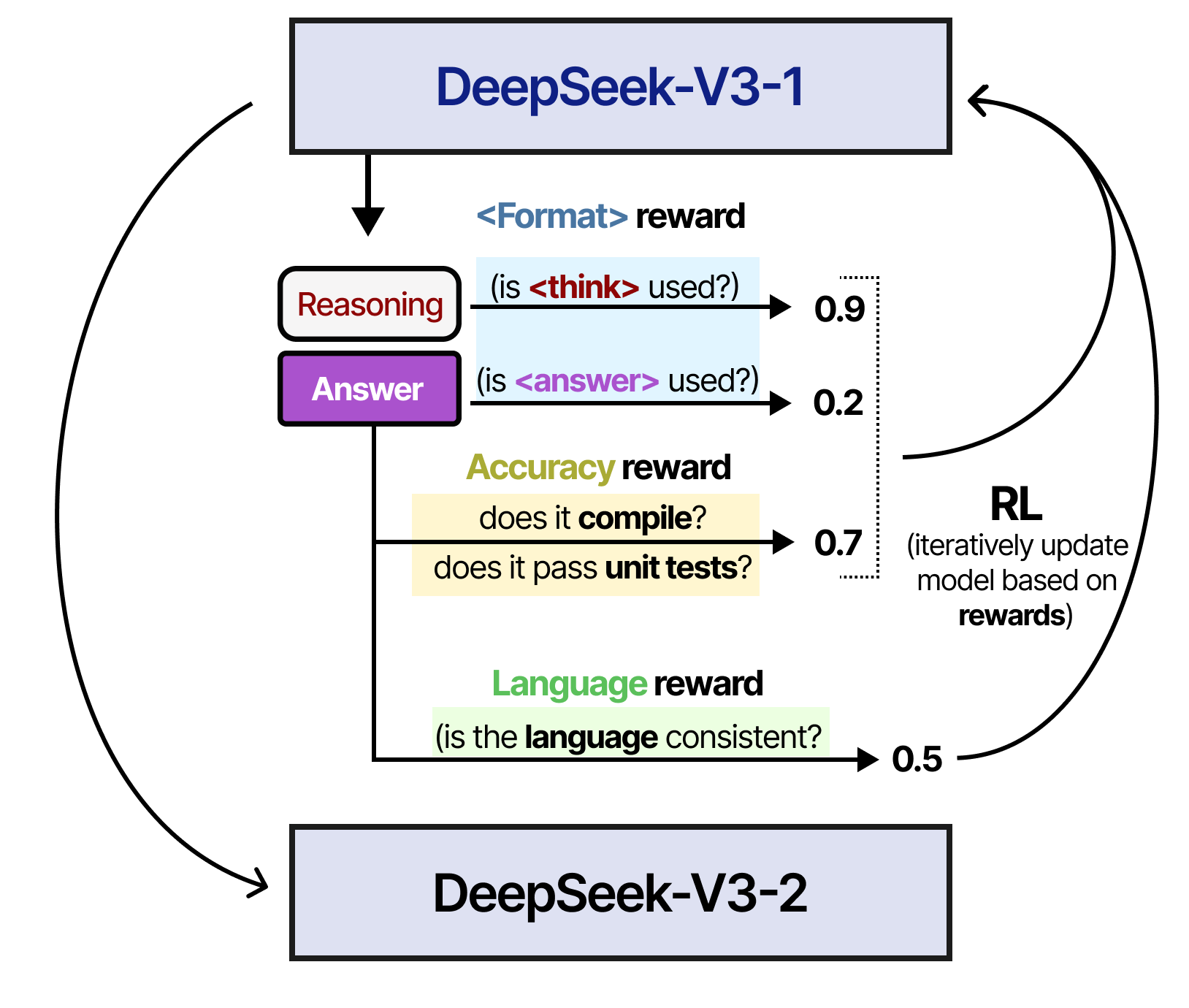
À l’étape 3, le modèle de l’étape 2 est utilisé pour générer des données de raisonnement synthétiques qui serviront à l’apprentissage supervisé de l’étape 4. Grâce à un filtrage (récompenses basées sur des règles) et à un modèle de récompense (DeepSeek-V3-Base), 600 000 échantillons de raisonnement de haute qualité sont alors créés. De plus, 200 000 échantillons de non raisonnement sont créés en utilisant DeepSeek-V3-Base.

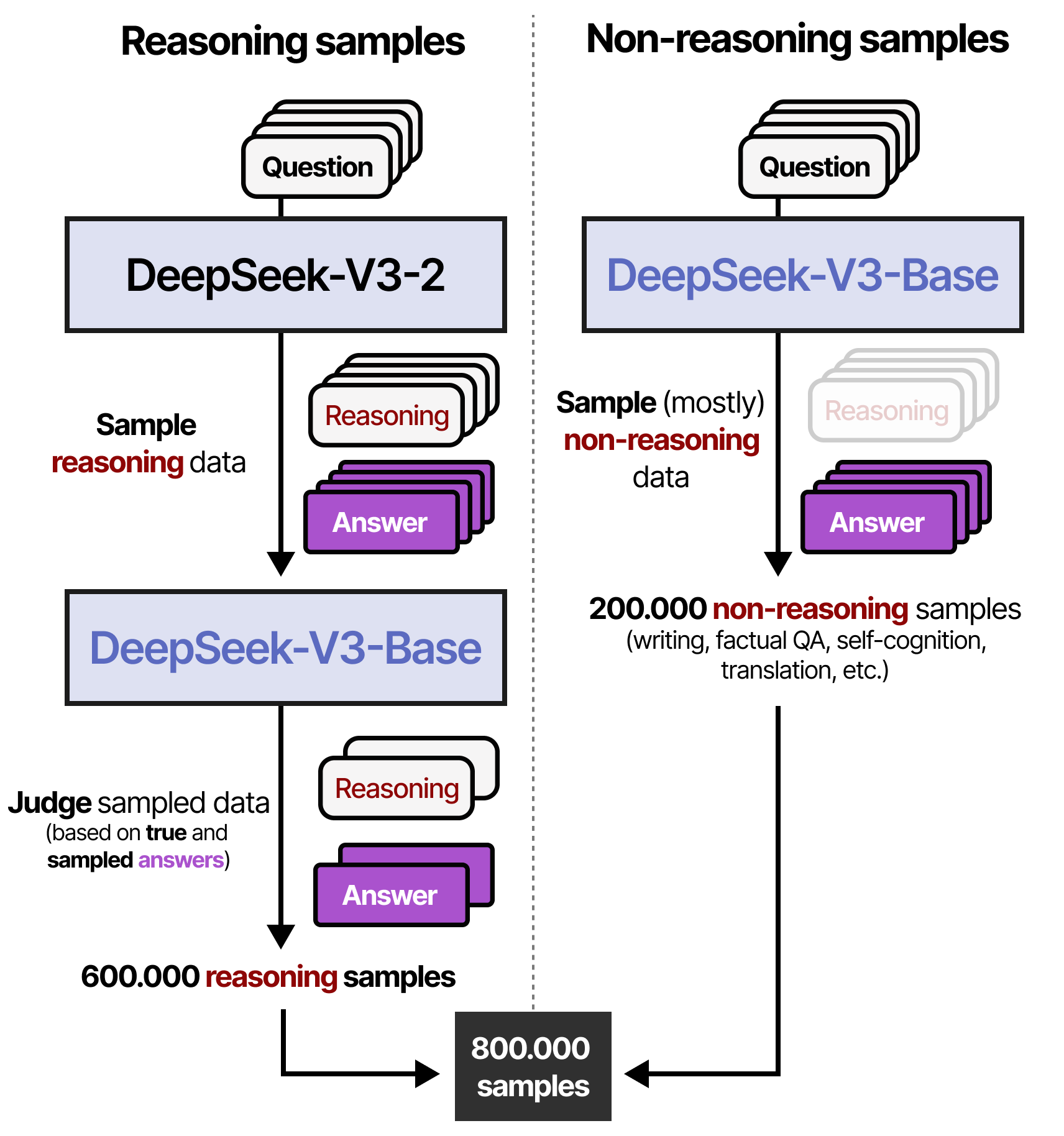
À l’étape 4, l’ensemble de données des 800 000 échantillons résultats de l’étape3 sont utilisés pour effectuer un finetuning supervisé du DeepSeek-V3-Base.

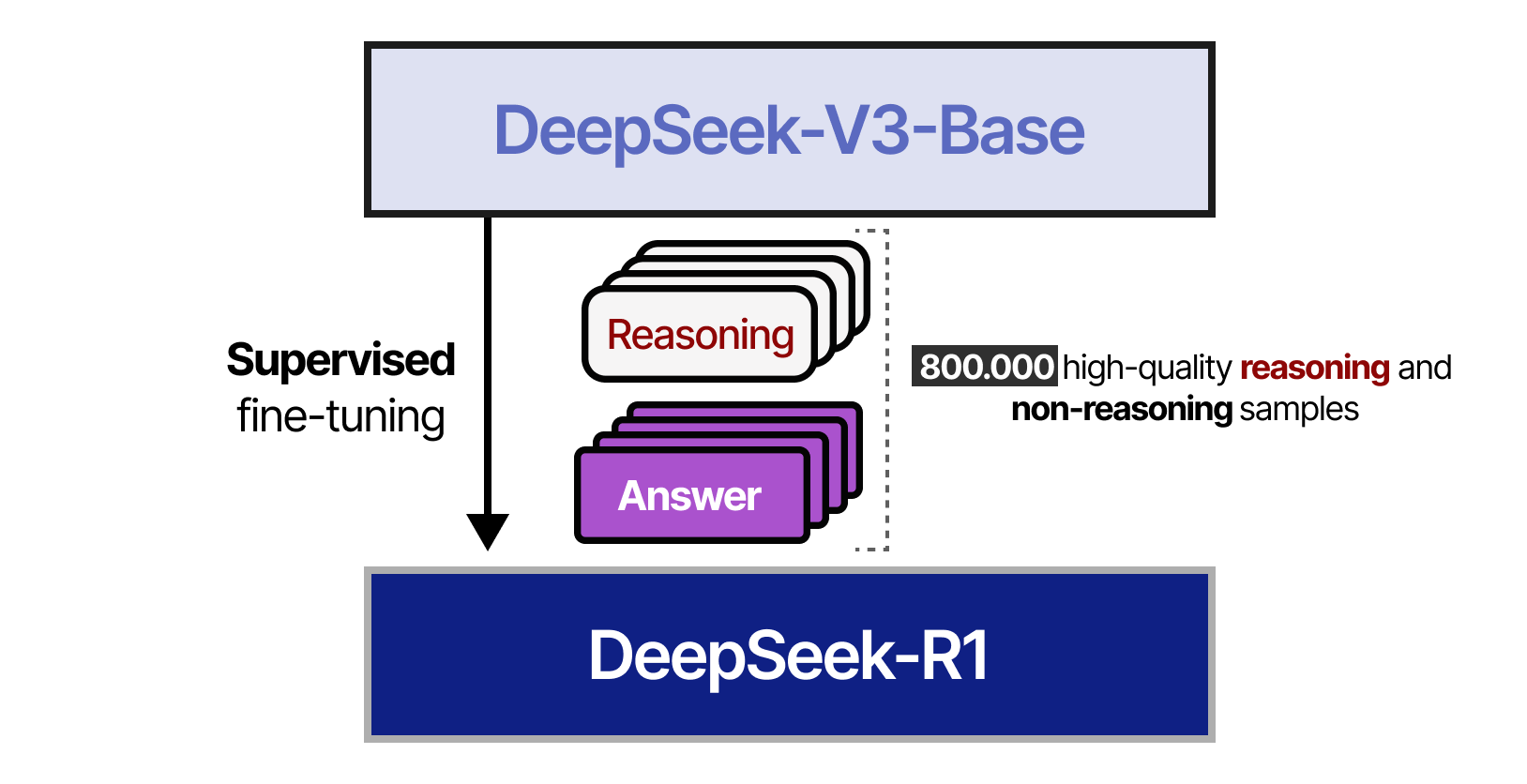
À l’étape 5, un entraînement par apprentissage par renforcement est effectué en utilisant une approche similaire à celle utilisée dans DeepSeek-R1-Zero. Cependant, pour l’aligner sur les préférences humaines, des signaux de récompense supplémentaires sont ajoutés, axés sur l’utilité et l’innocuité. Il est également demandé au modèle de résumer le processus de raisonnement afin d’éviter les problèmes de lisibilité.

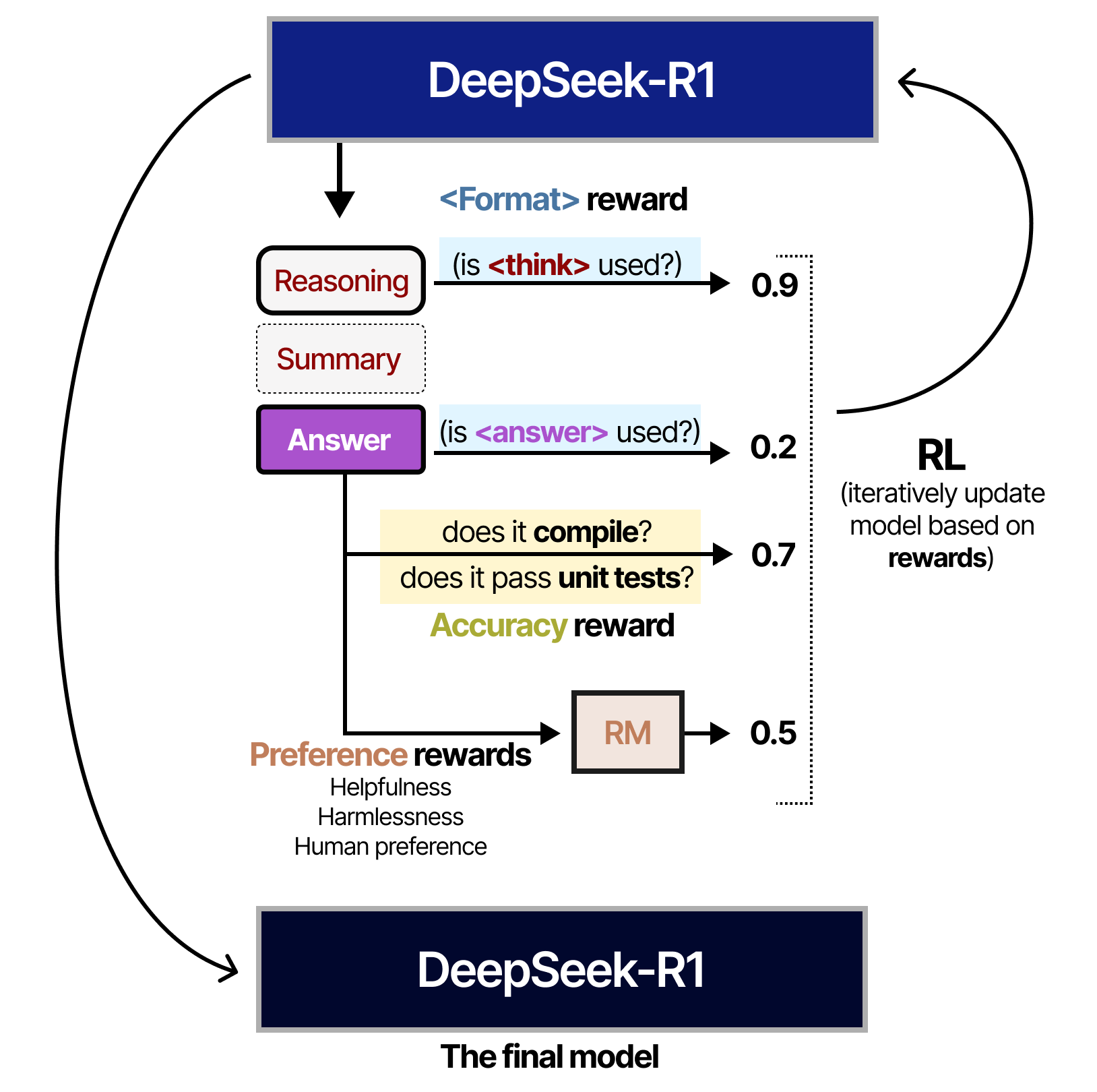
Et c’est tout ! Cela signifie que DeepSeek-R1 est en fait une spécialisation de DeepSeek-V3-Base grâce à un finetuning supervisé et à l’apprentissage par renforcement. Le plus gros du travail consiste à s’assurer que des échantillons de très grande qualité sont générés !

Distiller le raisonnement avec DeepSeek-R1

DeepSeek-R1 est un modèle énorme de 671Mds de paramètres. Cela signifie qu’il est impossible d’exécuter un tel modèle sur du matériel grand public. Heureusement, les auteurs ont étudié les moyens de distiller la qualité de raisonnement de DeepSeek-R1 dans d’autres modèles, tels que Qwen-32B, que nous pouvons faire tourner sur des GPU raisonnables ! Pour ce faire, ils utilisent le DeepSeek-R1 comme modèle d’enseignant et le plus petit modèle comme élève. Les deux modèles reçoivent une instruction et doivent générer une distribution de probabilité des tokens. Au cours de l’entraînement, l’élève tentera de suivre de près la distribution du professeur.

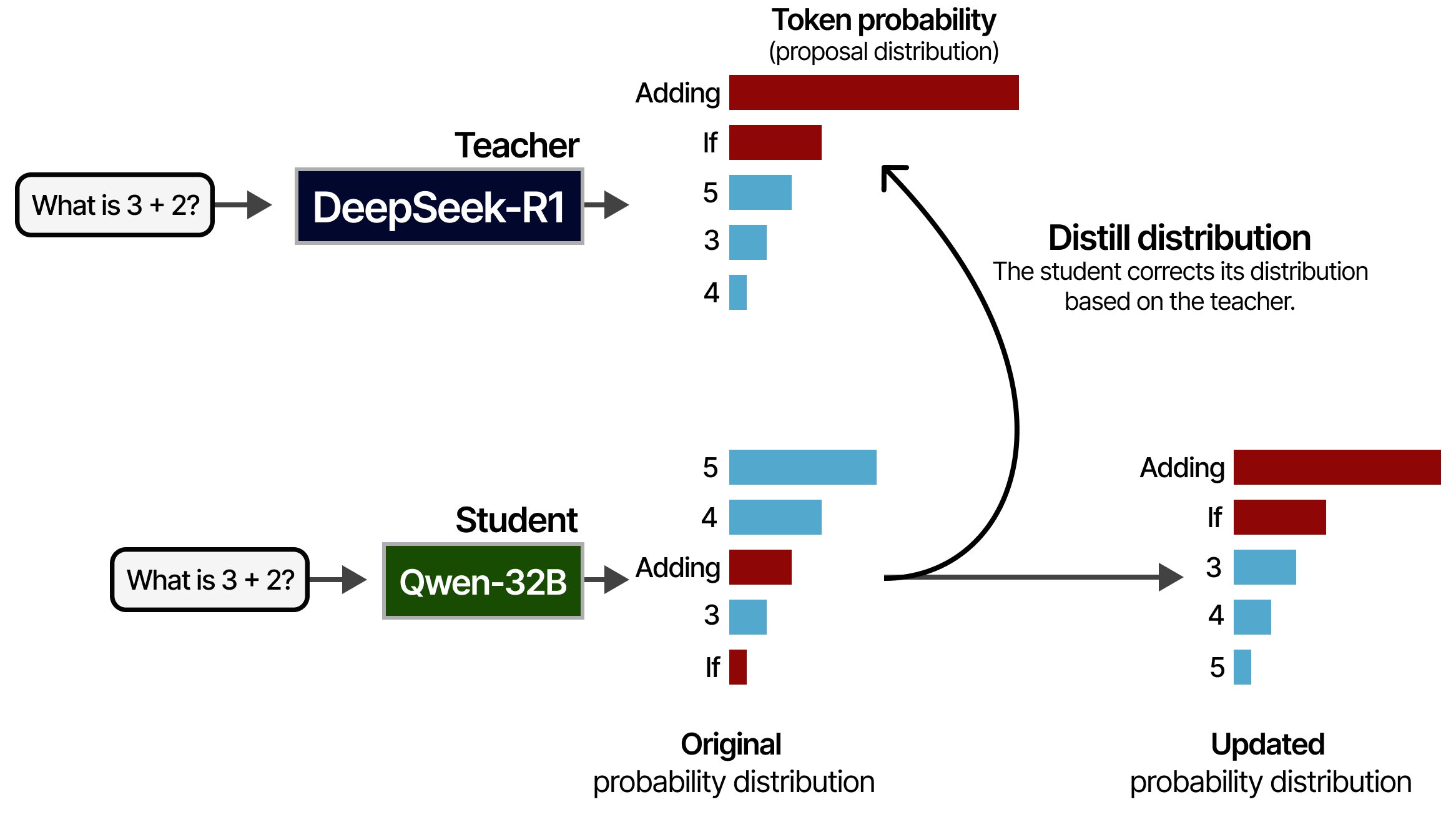
Ce processus a été réalisé à partir de l’ensemble des 800 000 échantillons de haute qualité que nous avons vus précédemment :

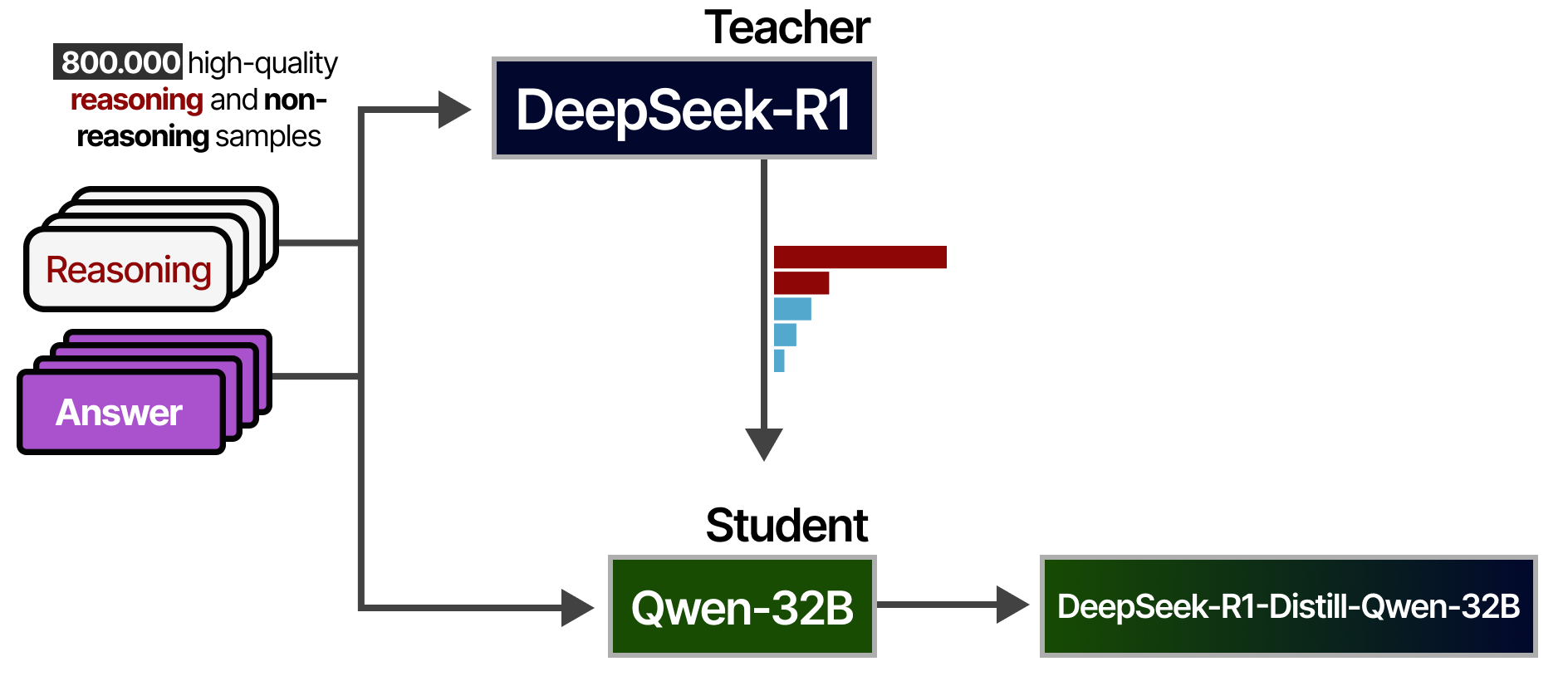
Les modèles distillés qui en résultent sont très performants puisqu’ils n’ont pas seulement appris à partir des 800 000 échantillons, mais aussi de la manière dont le professeur (DeepSeek-R1) y répondrait !

Tentatives infructueuses

Nous avons parlé plus haut des modèles de récompense de processus (PRM) et de la recherche arborescente de Monte Carlo. Il s’avère que DeepSeek a également essayé ces techniques pour inculquer le raisonnement au modèle mais sans succès. Avec la recherche arborescente de Monte Carlo, les auteurs ont rencontré des problèmes liés au vaste espace de recherche et ont dû limiter les expansions de nœuds. Avec les PRM pour les techniques Best-of-\(N\), ils ont rencontré des problèmes de surcharge de calcul en raison du réentraînement permanent du modèle de récompense afin d’empêcher le piratage des récompenses. Cela ne signifie pas que ces techniques ne sont pas valables, mais cela donne un aperçu intéressant des limites de ces techniques !


Conclusion

Ceci conclut notre voyage sur les LLM avec raisonnement. Nous espérons que cet article vous a permis de mieux comprendre le potentiel de la mise à l’échelle des calculs lors de la phase d’inférence. J’espère que cette introduction a été accessible. Si vous souhaitez aller plus loin sur ce sujet, je vous suggère les ressources suivantes :
• L’article The Illustrated DeepSeek-R1 est un guide sur DeepSeek-R1 par Jay ALAMMAR.
• Cet excellent article d’Hugging Face sur la mise à l’échelle des calculs lors de la phase d’inférence avec des expériences intéressantes.
• Cette vidéo de Sasha RUSH, est un excellent support pour entrer dans les détails techniques des techniques courantes de calcul de la phase d’inférence.


Références




Citation 

@inproceedings{LLM_raisonnement_blog_post,
author = {Loïck BOURDOIS},
title = {Un guide visuel sur les LLM avec raisonnement},
year = {2025},
url = {https://lbourdois.github.io/blog/LLM_raisonnement/}
}

Vous pourriez aimer aussi