Avant-propos Permalink

Cet article est une traduction de celui de Maarten Grootendorst : A Visual Guide to Mixture of Experts (MoE).
Maarten est co-auteur du livre Hands-On Large Language Models.

Introduction Permalink

Dans cet article, nous allons prendre le temps d’explorer la composante importante, qu’est le mélange d’experts ou MoE (pour mixture of experts), à travers plus de 50 visualisations !
Nous passerons en revue les deux principaux composants d’un MoE, à savoir les experts et le routeur, tels qu’ils sont appliqués dans les architectures basées sur les grands modèles de langue ou LLM (pour Large Language Model).

Qu’est-ce qu’un mélange d’experts ? Permalink

Le mélange d’experts est une technique qui utilise de nombreux sous-modèles différents (ou « experts ») pour améliorer la qualité des LLM. Deux éléments principaux définissent un MoE :
• Experts - Chaque couche FFNN dispose alors d’un ensemble d’experts dont un sous-ensemble peut être choisi. Ces experts sont généralement des eux-mêmes FFNN.
• Routeur - Détermine quels tokens sont envoyés à quels experts.
Dans chaque couche d’un LLM avec un MoE, nous trouvons des experts (quelque peu spécialisés) :

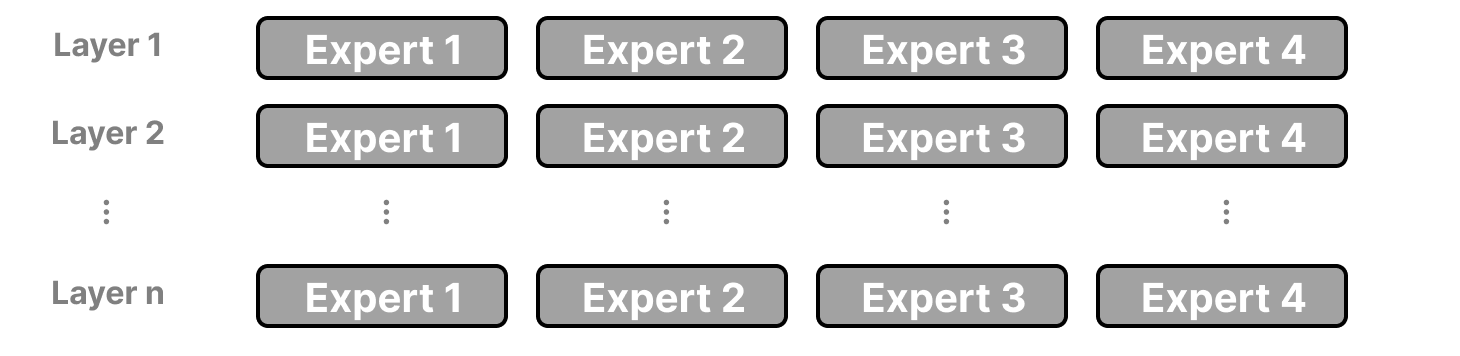
Il faut savoir qu’un expert n’est pas spécialisé dans un domaine spécifique comme la psychologie ou la biologie par exemple. Il apprend tout au plus des informations syntaxiques au niveau du mot :

Plus précisément, leur expertise porte sur le traitement de tokens spécifiques dans des contextes spécifiques. Le routeur sélectionne le(s) expert(s) le(s) mieux adapté(s) à une entrée donnée :

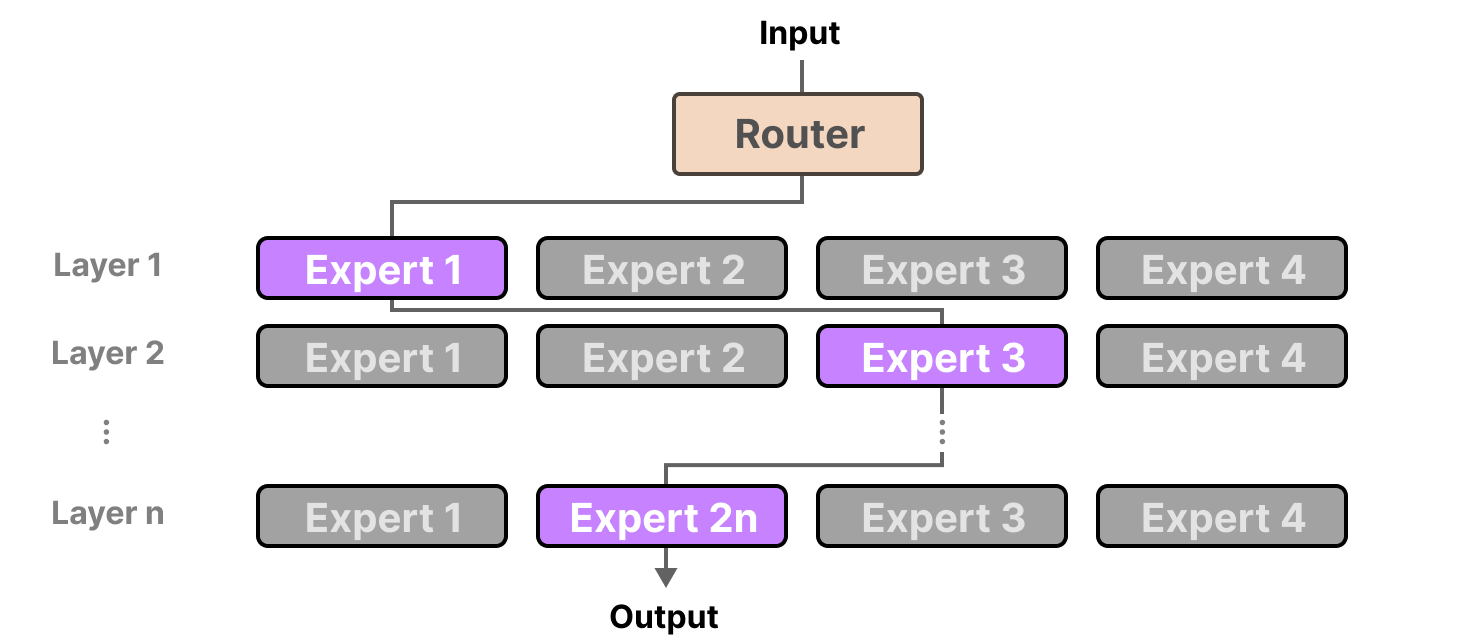
Chaque expert n’est pas un LLM complet mais un sous-modèle faisant partie de l’architecture du LLM.

Les experts Permalink

Pour explorer ce que les experts représentent et comment ils fonctionnent, examinons d’abord ce que le MoE est censé remplacer : les couches denses.

Couches denses Permalink

Le mélange d’experts part d’une fonctionnalité relativement basique des LLM, à savoir le Feedforward Neural Network (FFNN).
Rappelons qu’un transformer-décodeur (i.e. un GPT) standard applique le FFNN après la couche de normalisation :

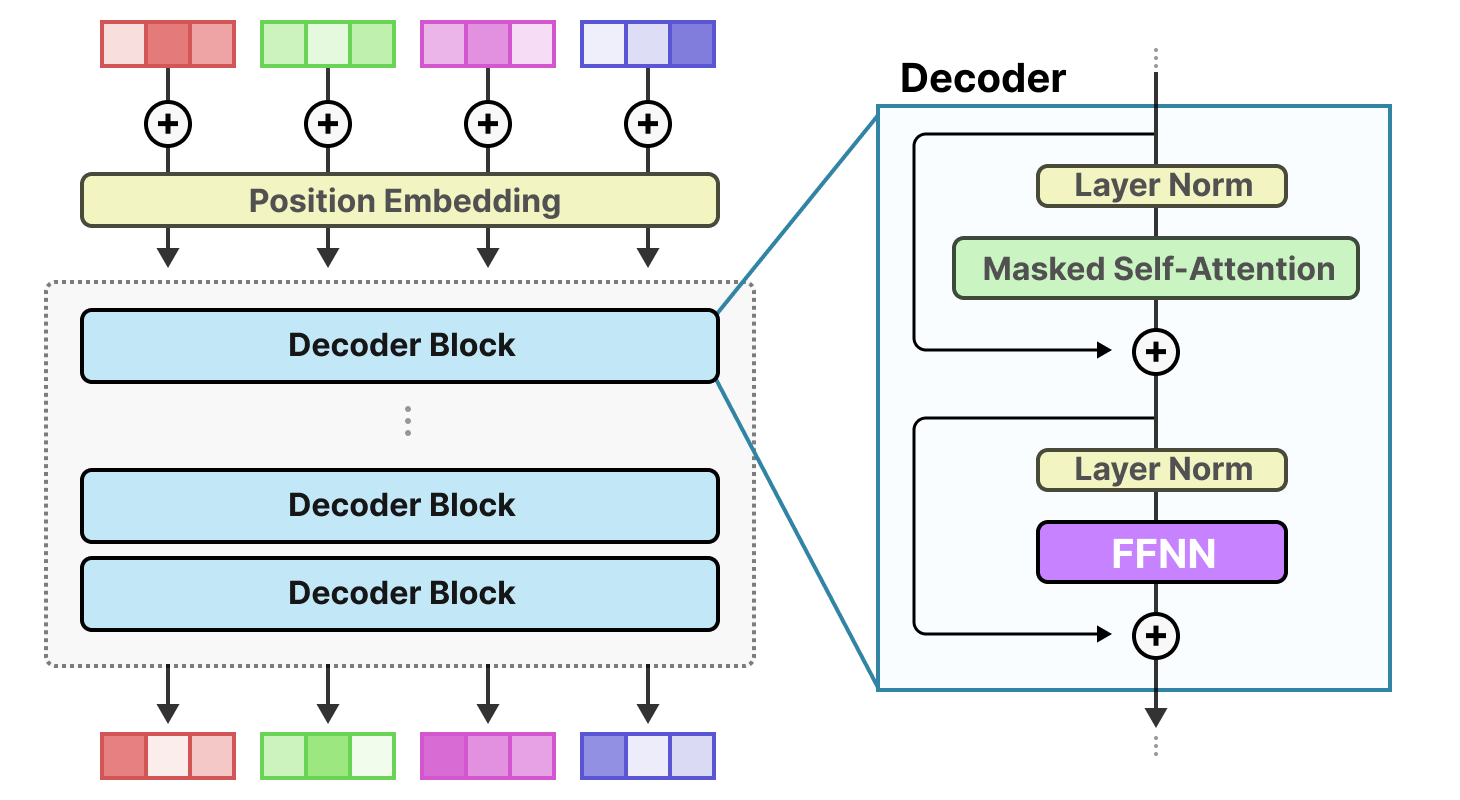
Un FFNN permet au modèle d’utiliser les informations contextuelles créées par le mécanisme d’attention, en les transformant davantage pour saisir des relations plus complexes dans les données.
Cependant, le FFNN croît rapidement en taille. Pour apprendre ces relations complexes, il étend généralement les données qu’il reçoit :

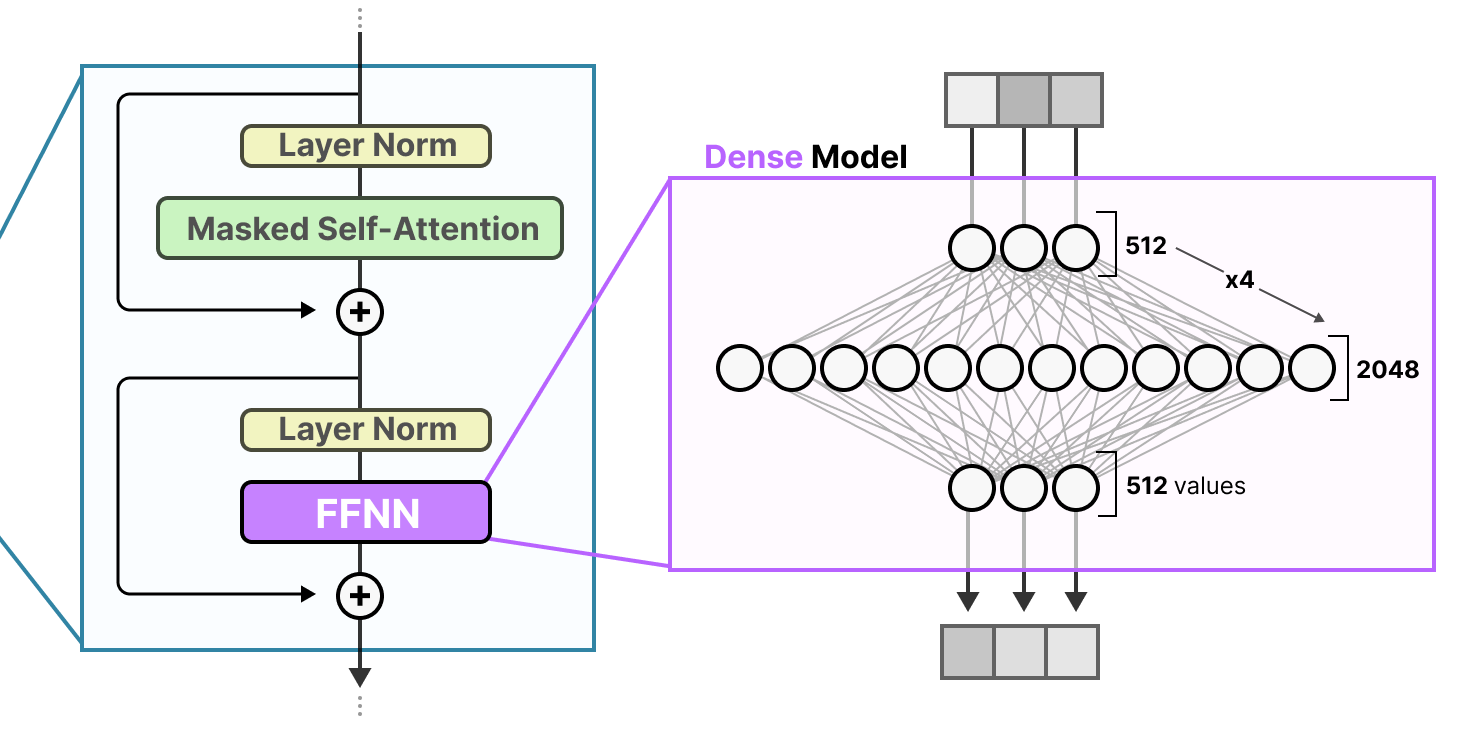
Couches éparses Permalink

Le FFNN dans un transformer standard est appelé un modèle dense puisque tous les paramètres (ses poids et ses biais) sont activés. Rien n’est oublié et tout est utilisé pour calculer la sortie.
Si nous examinons de plus près le modèle dense, nous remarquons que l’entrée active tous les paramètres dans une certaine mesure :

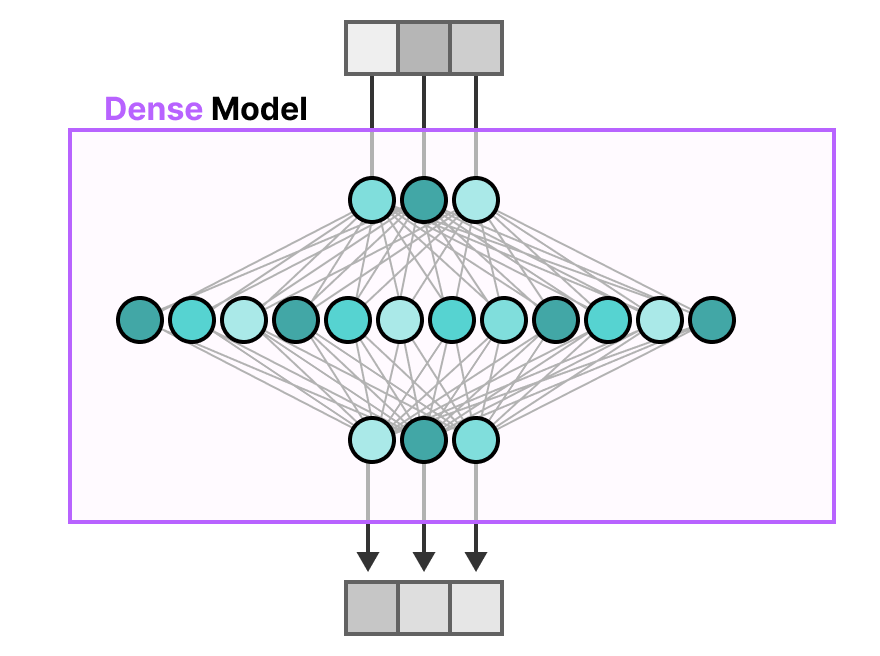
Au contraire, les modèles épars n’activent qu’une partie de l’ensemble de leurs paramètres et sont étroitement liés au mélange d’experts.
Pour illustrer ceci, nous pouvons découper notre modèle dense en morceaux (appelés experts), le réentraîner et n’activer qu’un sous-ensemble d’experts à un moment donné :

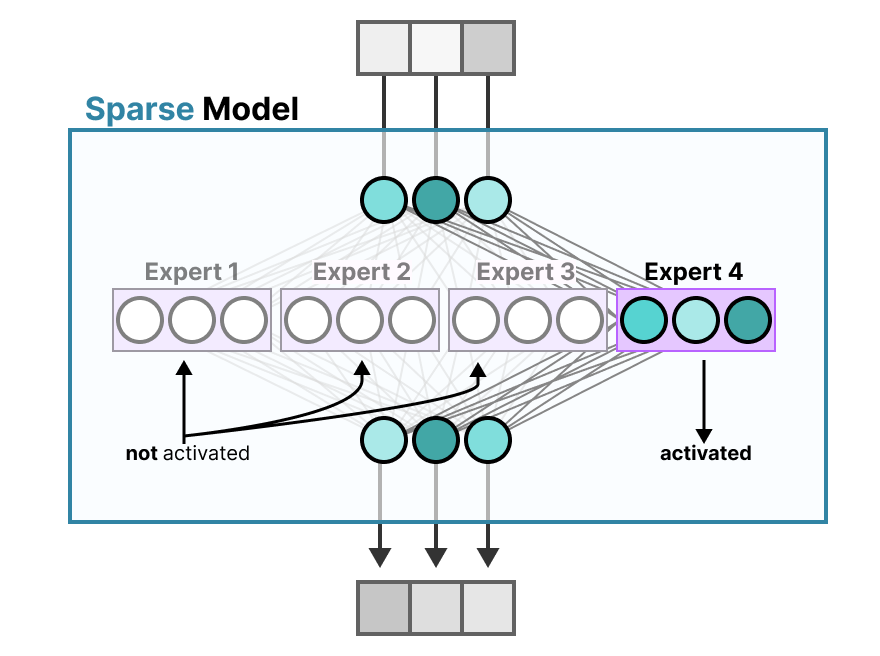
L’idée sous-jacente est que chaque expert apprend des informations différentes au cours de l’entraînement. Ensuite, lors de l’inférence, seuls des experts spécifiques sont utilisés car ils sont les plus pertinents pour une tâche donnée.
Lors d’une question, nous pouvons sélectionner l’expert le mieux adapté à une tâche donnée :

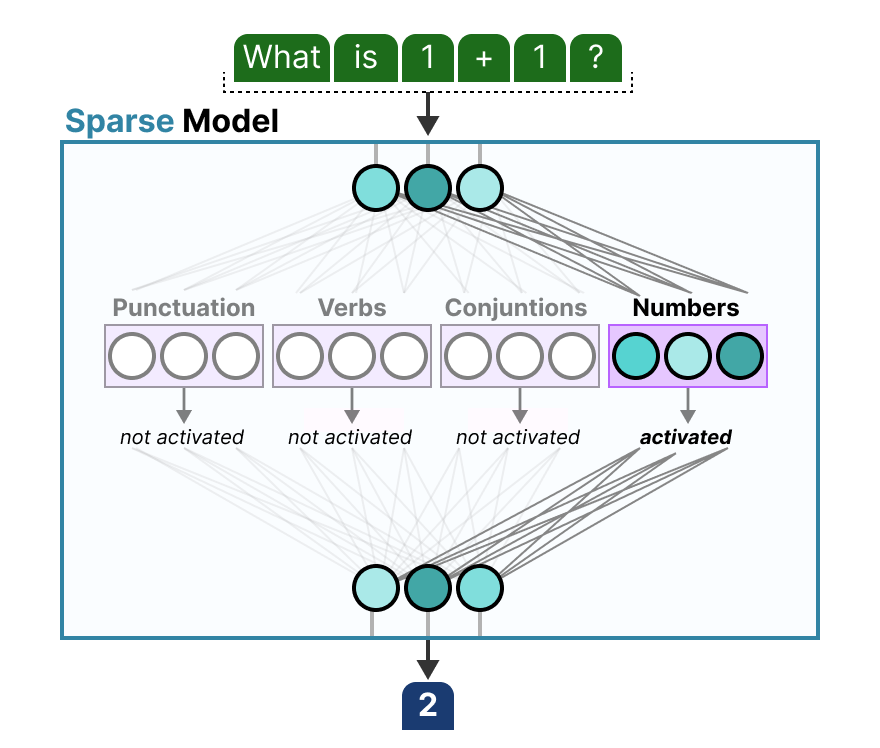
Qu’est-ce qu’apprend un expert? Permalink

Comme l’avons indiqué, les experts apprennent des informations plus fines que des domaines entiers (voir notamment le papier ST-MoE: Designing stable and transferable sparse expert models de ZOPH, BELLO, FEDUS et al. (2022)). C’est pourquoi les qualifier d’ « experts » a parfois été considéré comme trompeur.

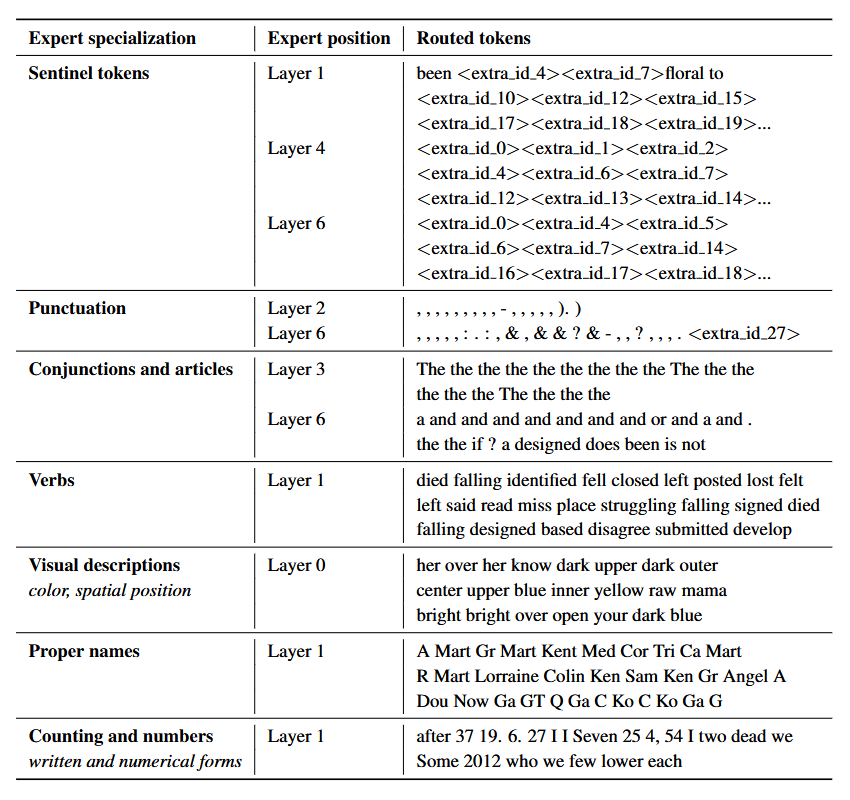
Les experts de modèle décodeur ne semblent toutefois pas avoir le même type de spécialisation. Cela ne signifie pas pour autant que tous les experts sont égaux.
Un bon exemple se trouve dans le papier Mixtral of Experts de Mistral (2024) où chaque token est surligné avec le premier choix de l’expert.

Ainsi, bien que les experts d’un décodeur ne semblent pas avoir de spécialisation, ils apparaissent être utilisés de manière cohérente pour certains types de tokens.

L’architecture des experts Permalink

Bien qu’il soit agréable de voir les experts comme une couche cachée d’un modèle dense découpé en morceaux, ils sont souvent eux-mêmes des FFNN entiers :

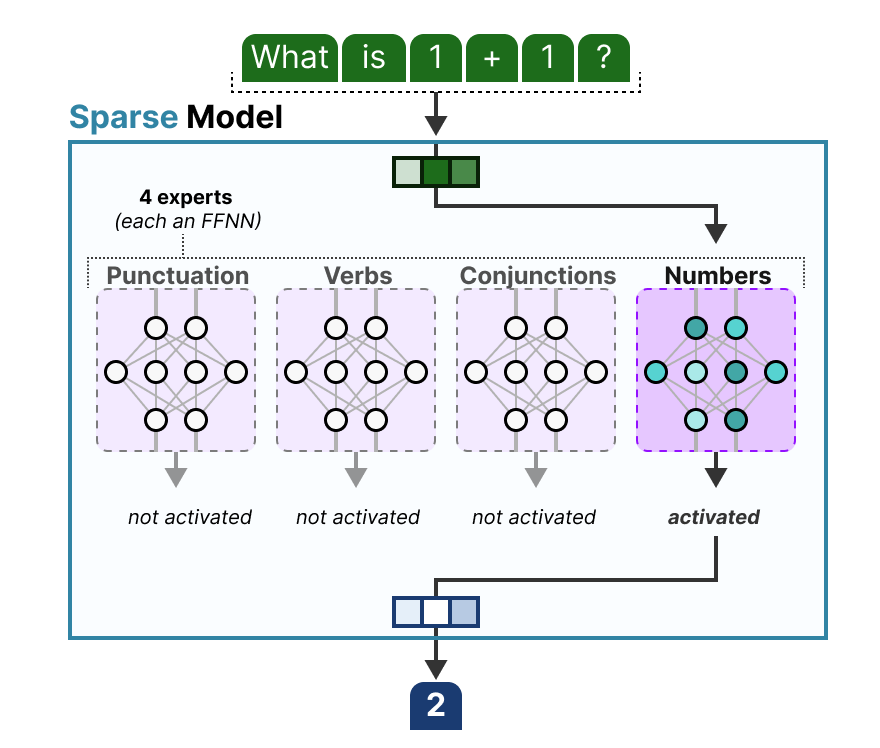
Comme la plupart des LLM sont un empilement de plusieurs blocs décodeur, une entrée passera par plusieurs experts avant de générer la sortie :

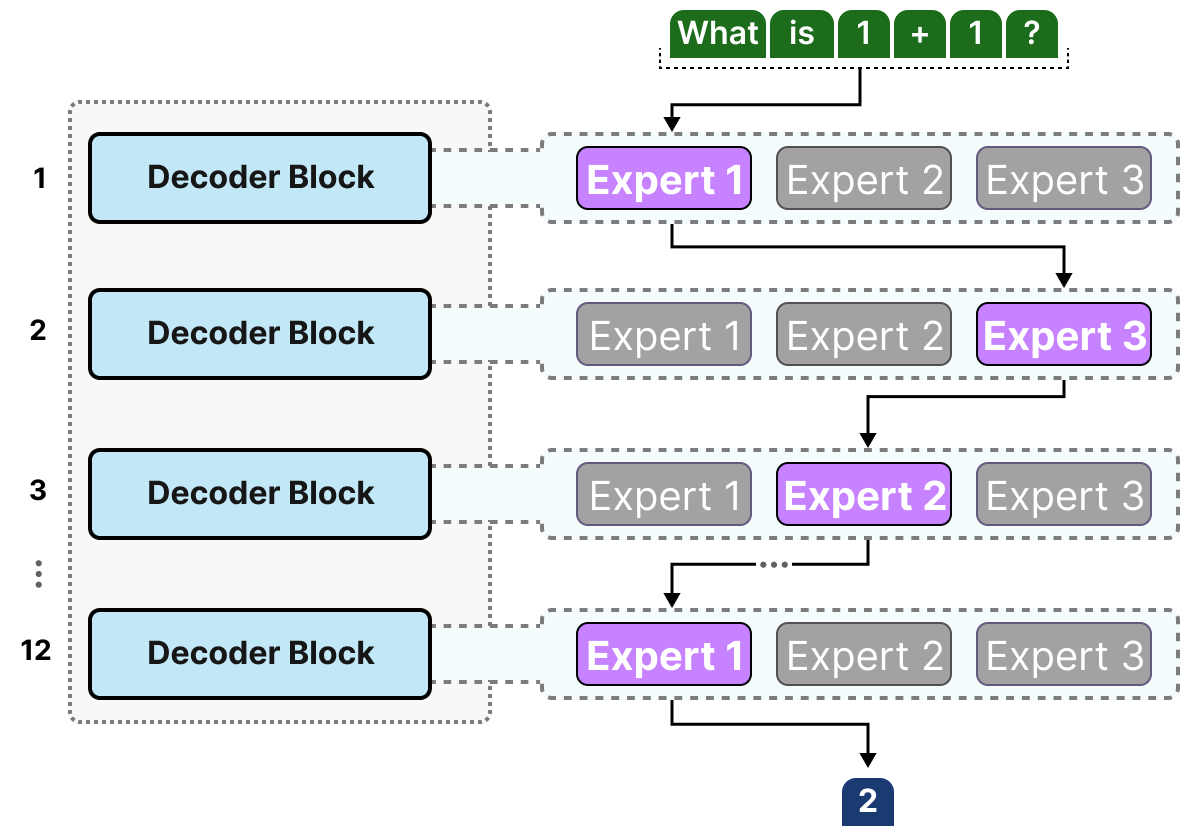
Les experts choisis diffèrent probablement d’un token à l’autre, ce qui se traduit par des « chemins » différents :

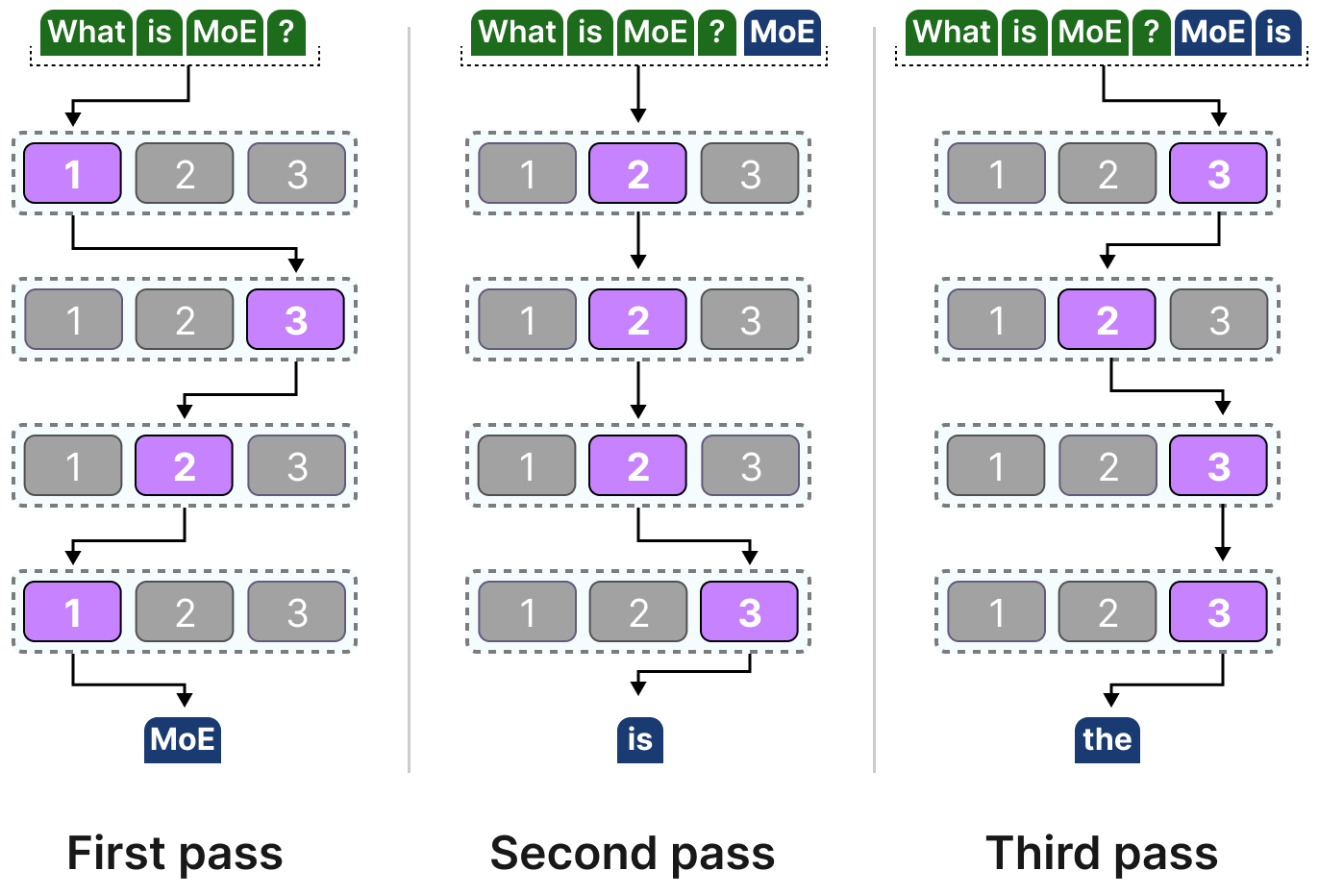
Si nous modifions notre visualisation du bloc décodeur, ce dernier contiendra désormais davantage de FFNN (un pour chaque expert) :

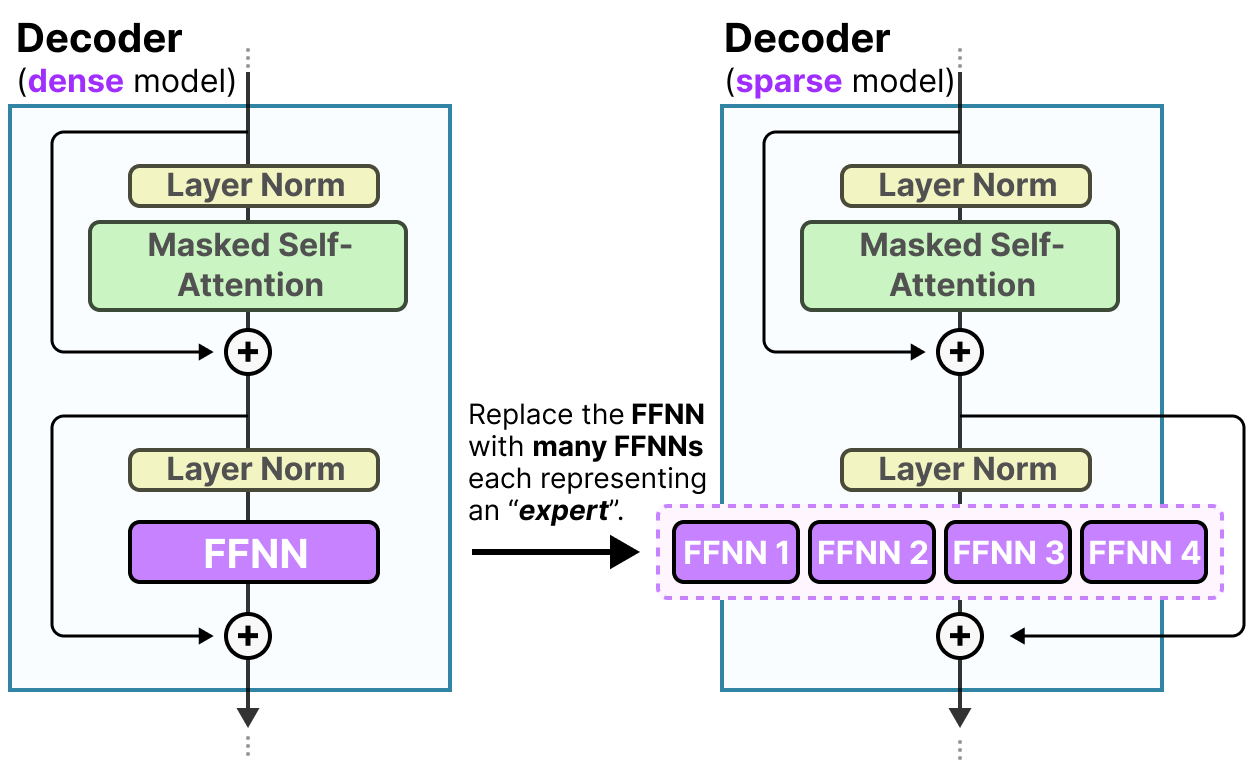
Le bloc décodeur dispose désormais de plusieurs FFNN (chacun étant un expert) qu’il peut utiliser lors de l’inférence.

Le mécanisme de routage Permalink

Maintenant que nous disposons d’un ensemble d’experts, comment le modèle sait-il quels experts utiliser ?
Juste avant les experts, un routeur (également appelé réseau de portes) est ajouté ; il est entraîné à sélectionner l’expert à choisir pour un token donné.

Le routeur Permalink

Le routeur est également un FFNN. Il est utilisé pour sélectionner l’expert le plus adapté en fonction d’une entrée particulière via les probabilités qu’il produit :

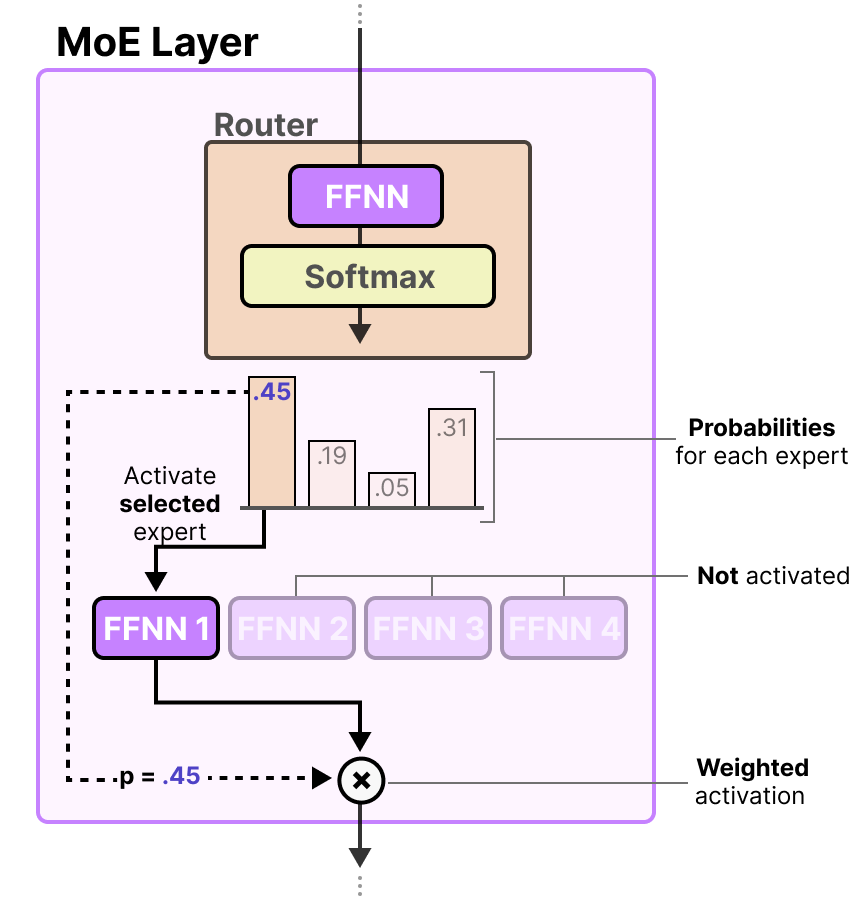
La couche expert renvoie la sortie de l’expert sélectionné multipliée par la valeur de la porte (probabilités de sélection).
Le routeur et les experts (dont seuls quelques-uns sont sélectionnés) constituent la couche MoE :

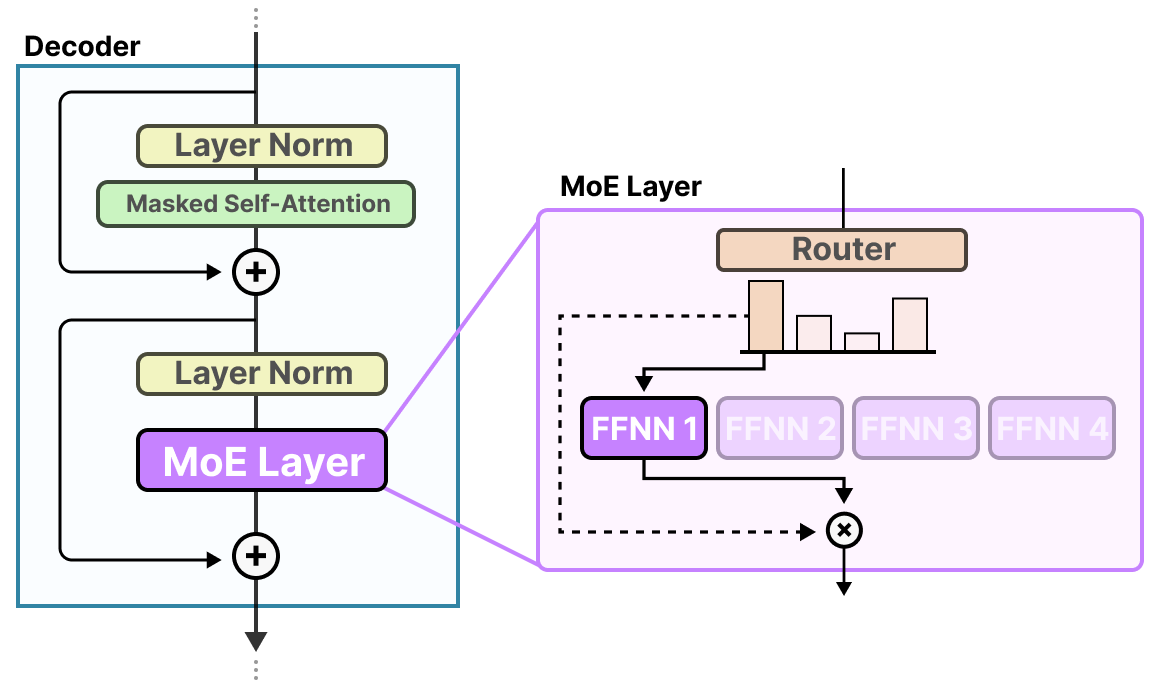
Une couche de MoE donnée peut être de deux tailles, soit éparse, soit dense.
Toutes deux utilisent un routeur pour sélectionner les experts, mais un MoE épars n’en sélectionne que quelques-uns, tandis qu’un MoE dense les sélectionne tous, mais potentiellement selon des distributions différentes.

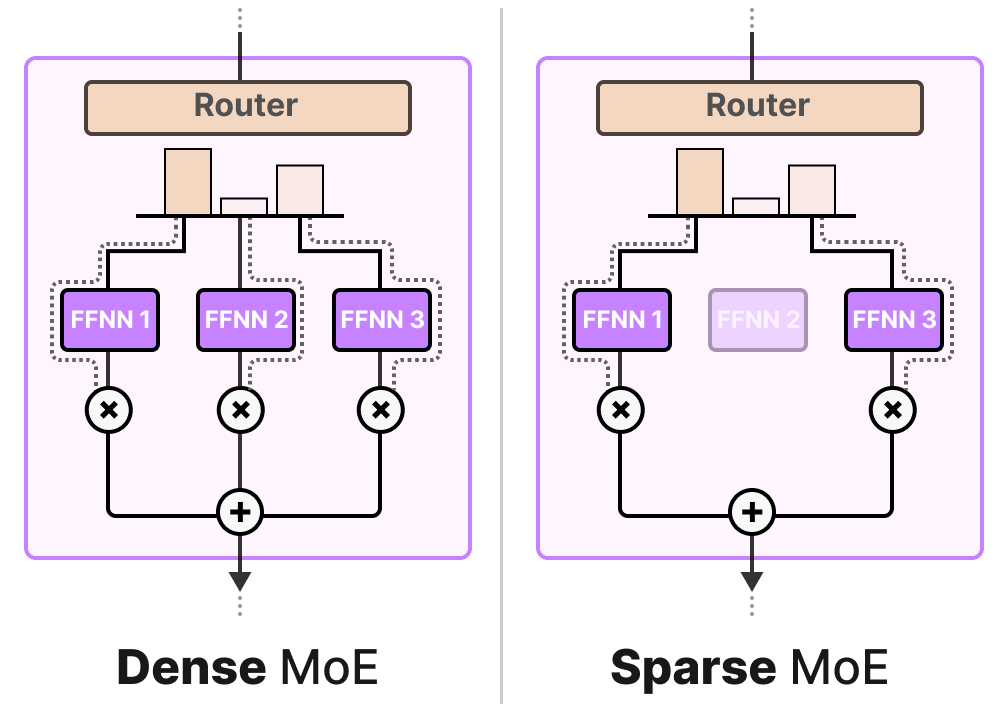
Par exemple, étant donné un ensemble de tokens, un MoE dense répartira les tokens entre tous les experts, tandis MoE épars n’en sélectionnera que quelques-uns.
Dans l’état actuel des LLM, lorsque vous voyez un mélange d’experts, il s’agit généralement d’un MoE épars car il vous permet d’utiliser un sous-ensemble d’experts. Cette méthode est moins coûteuse en termes de calcul, ce qui est une caractéristique importante pour les LLM.

Sélection des experts Permalink

Le réseau à portes est sans doute le composant le plus important de tout MoE car il décide non seulement des experts à sélectionner lors de l’inférence, mais aussi lors de l’entraînement.
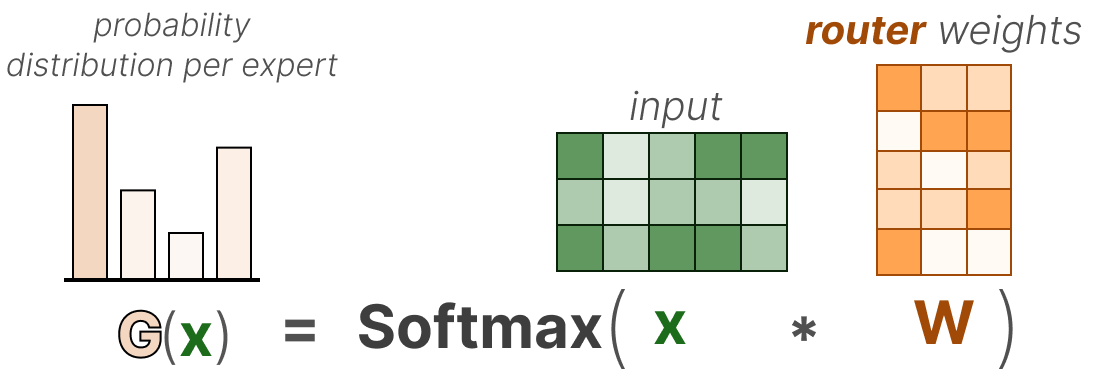
Dans sa forme la plus élémentaire, nous multiplions l’entrée (x) par la matrice de poids du routeur (W):

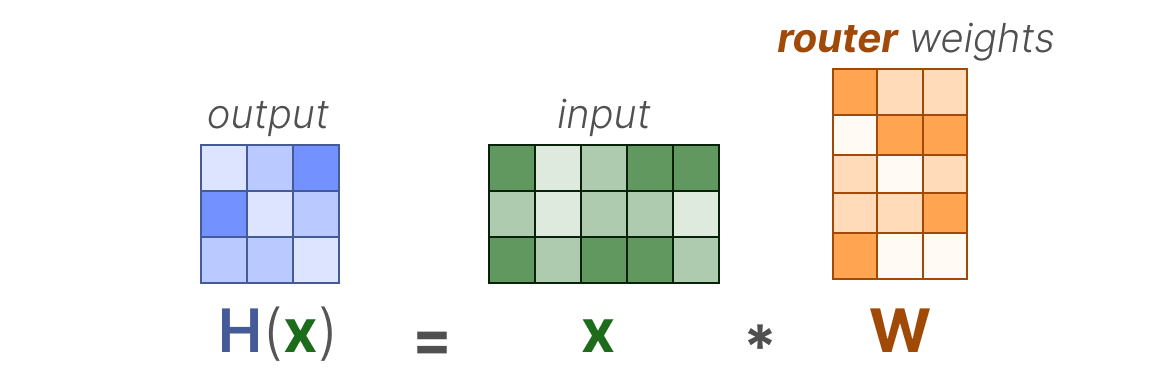
Ensuite, nous appliquons une fonction SoftMax sur la sortie pour créer une distribution de probabilité G(x) par expert :

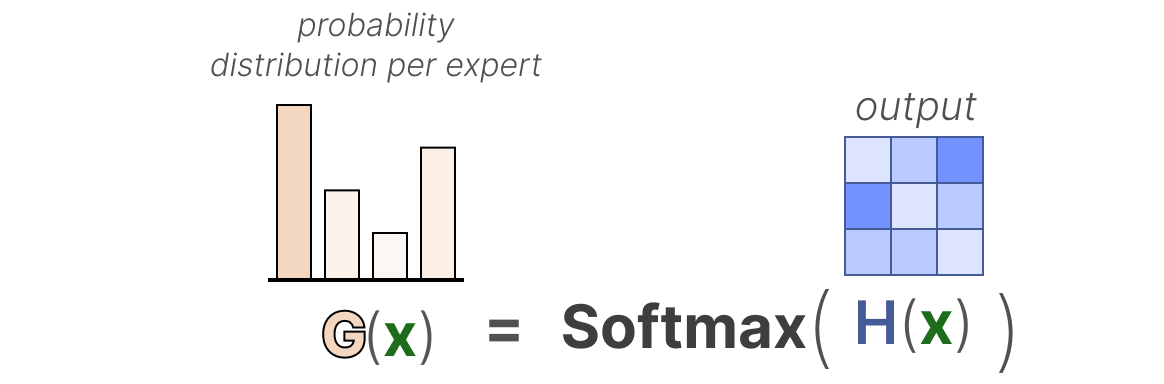
Le routeur utilise cette distribution de probabilité pour choisir le meilleur expert correspondant à une entrée donnée.
Enfin, nous multiplions la sortie de chaque routeur par chaque expert sélectionné et nous additionnons les résultats.

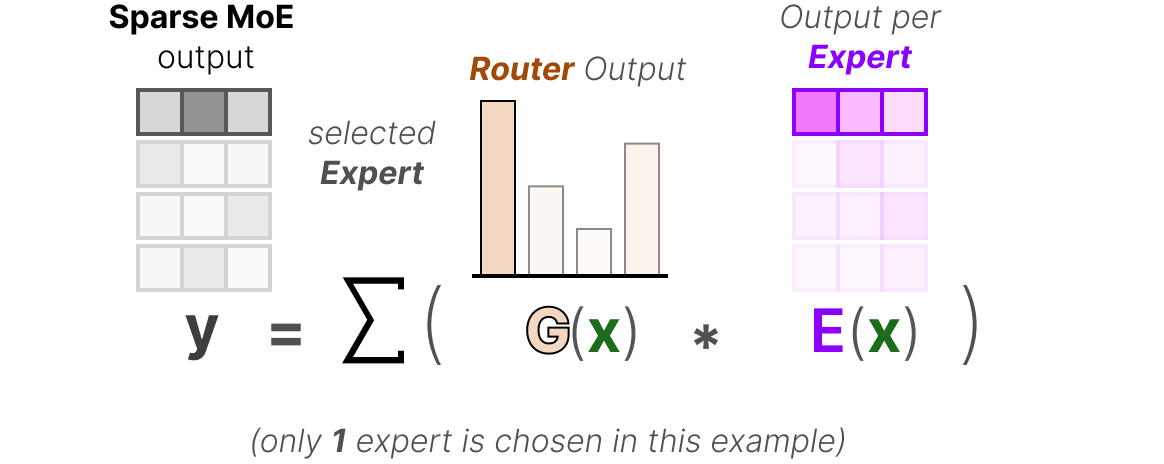
Assemblons le tout et explorons la manière dont l’entrée passe par le routeur et les experts :

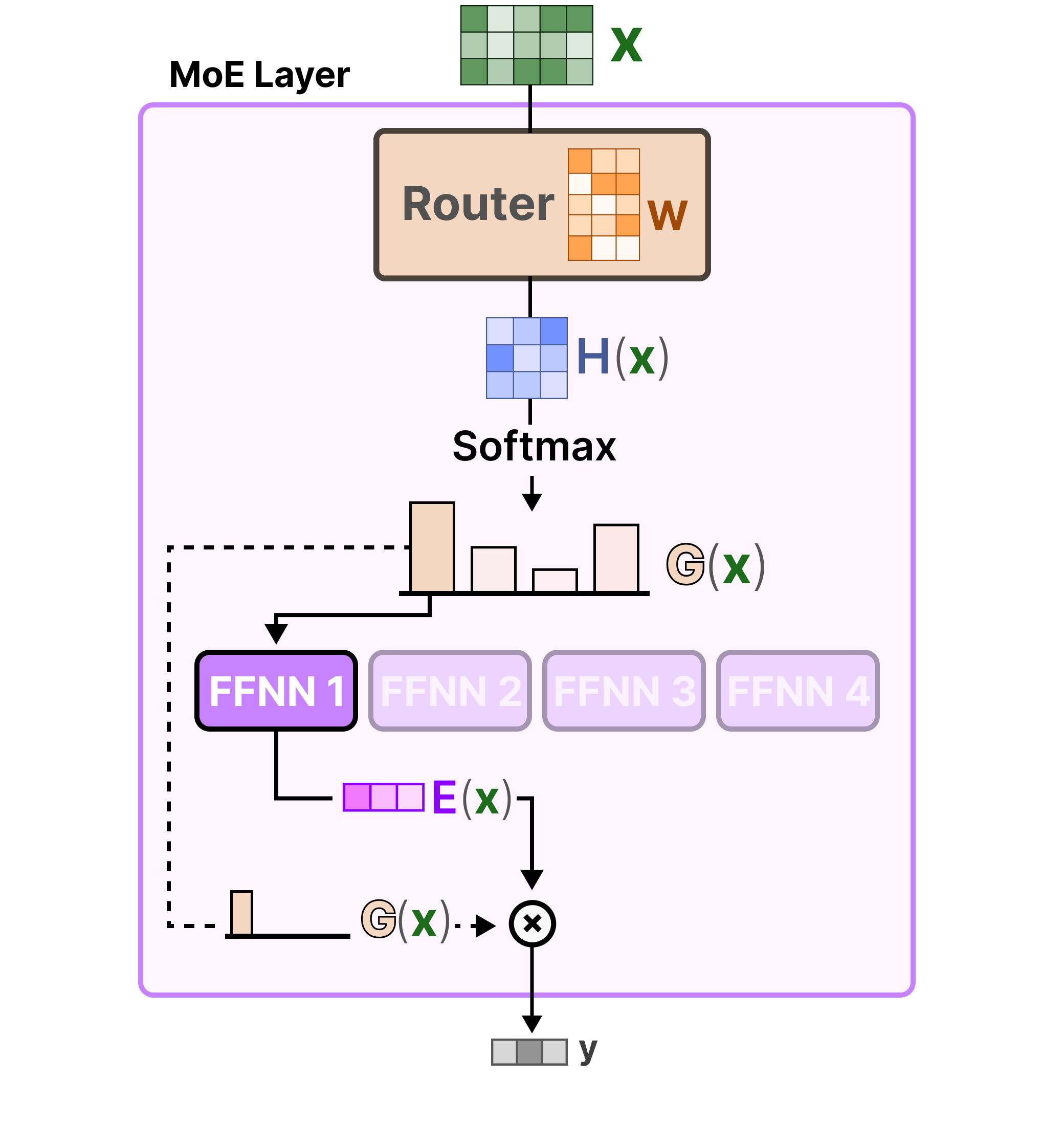
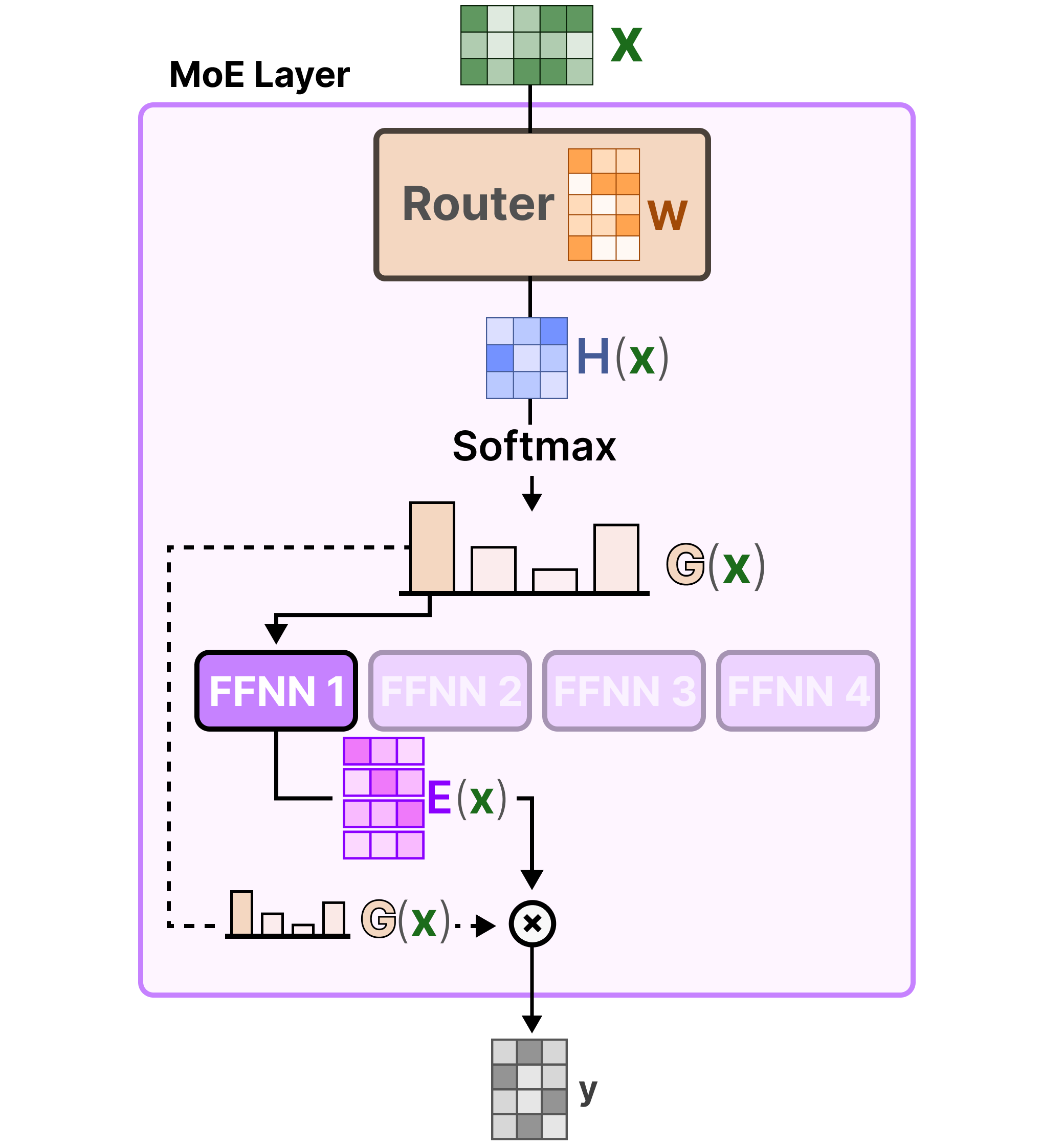
La complexité du routage Permalink

Toutefois, cette fonction simple conduit souvent le routeur à choisir le même expert car certains experts peuvent apprendre plus vite que d’autres :

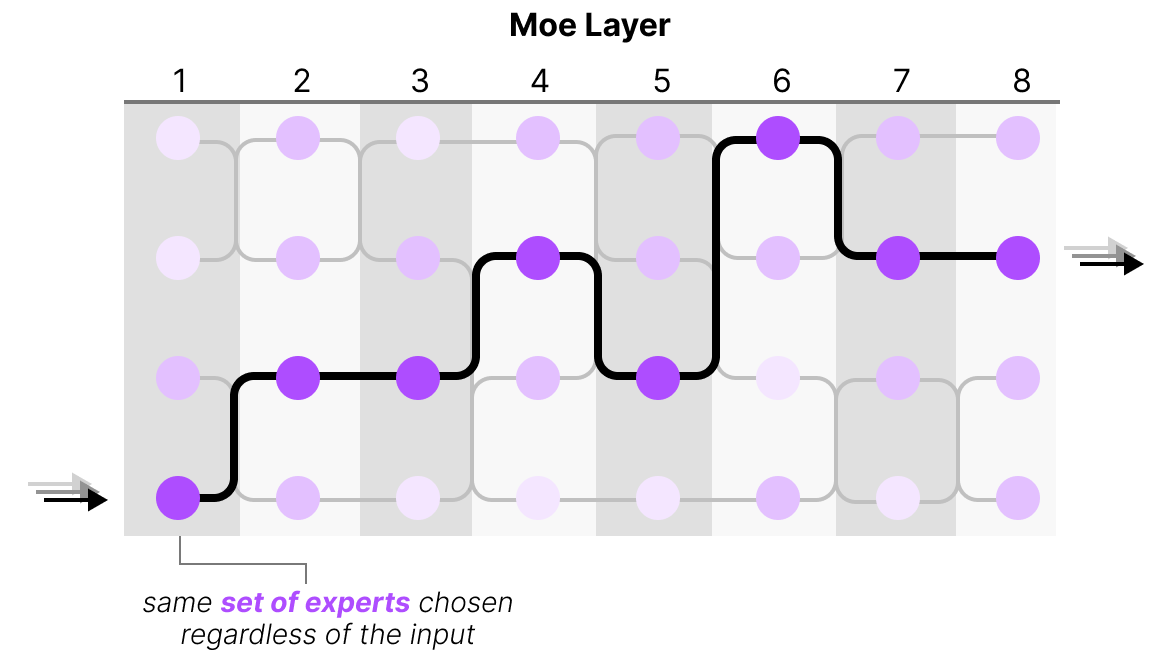
Non seulement la distribution des experts choisis sera inégale, mais certains experts ne seront pratiquement pas entraînés. Il en résulte des problèmes tant au niveau de l’entraînement que de l’inférence.
Au contraire, nous voulons que les experts aient la même importance pendant l’entraînement et l’inférence, ce que nous appelons l’équilibrage de la charge. D’une certaine manière, il s’agit d’éviter le surentraînement des mêmes experts.

Équilibrage de la charge Permalink

Pour équilibrer l’importance des experts, nous devons examiner le routeur qui est le principal élément permettant de décider quels experts choisir à un moment donné.

KeepTopK Permalink

Une méthode pour équilibrer la charge du routeur consiste à utiliser une méthode simple appelée KeepTopK par SHAZEER, MIRHOSEINI, MAZIARZ et al. (2017). En introduisant un bruit (gaussien) entraînable, nous pouvons éviter que les mêmes experts soient toujours sélectionnés :

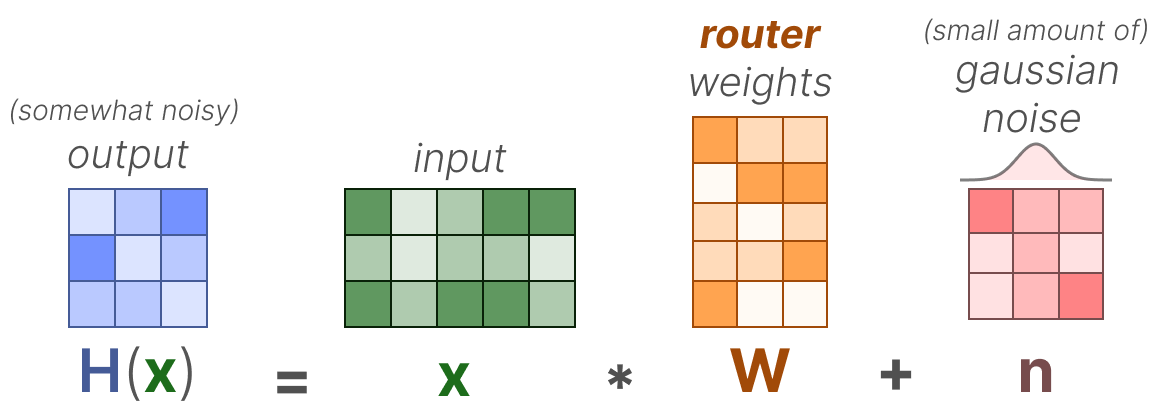
Ensuite, les poids de tous les experts, sauf les $k$ premiers que vous souhaitez activer (par exemple $2$), seront fixés à $-∞$ :

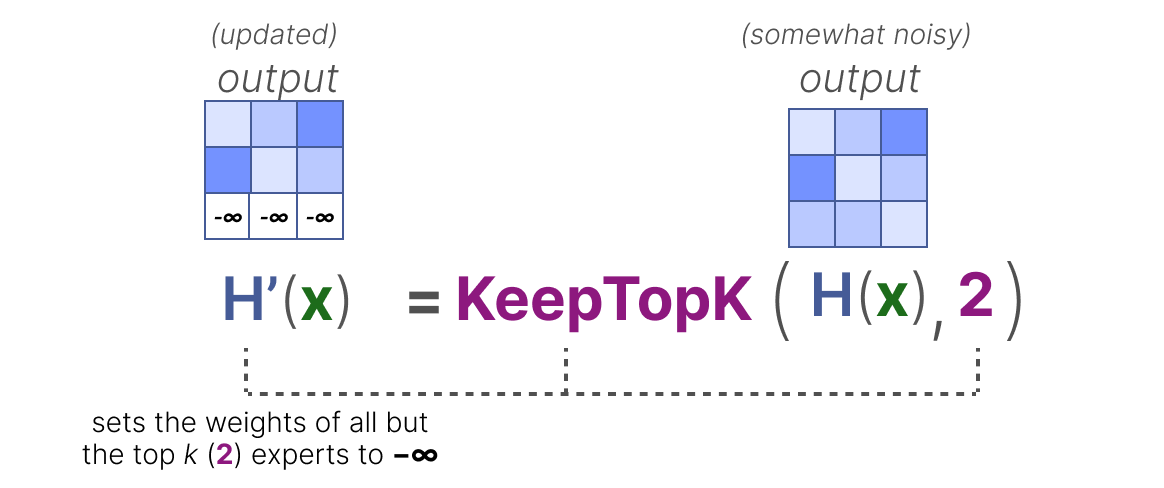
En fixant ces poids à $-∞$, la sortie de la fonction SoftMax sur ces poids se traduira par une probabilité de $0$ :

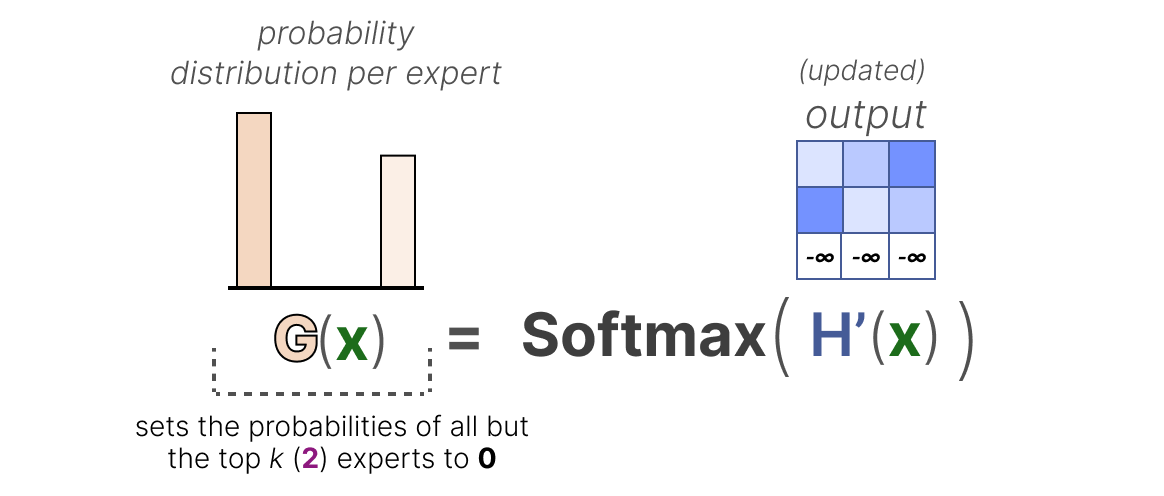
L’approche KeepTopK est une stratégie que de nombreux LLM utilisent encore malgré de nombreuses alternatives prometteuses. Notez qu’elle peut également être utilisée sans le bruit supplémentaire.

Choix des tokens Permalink

L’approche KeepTopK achemine chaque token vers quelques experts sélectionnés. Cette méthode, appelée « Token Choice », permet d’envoyer un token donné à un seul expert (routage top-$1$) :

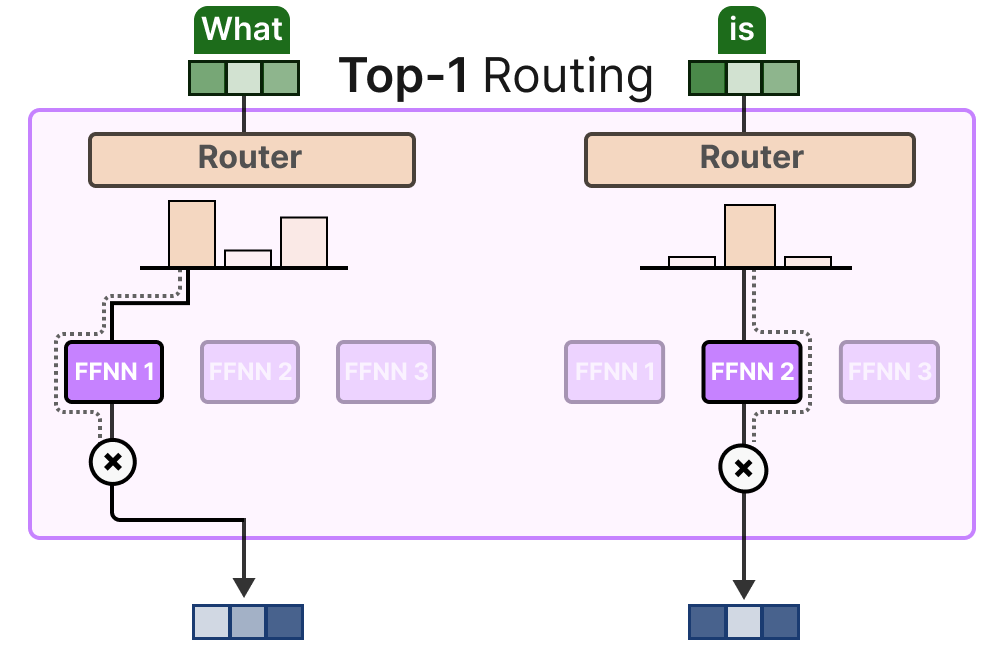
ou à plusieurs experts (routage top-$k$) :

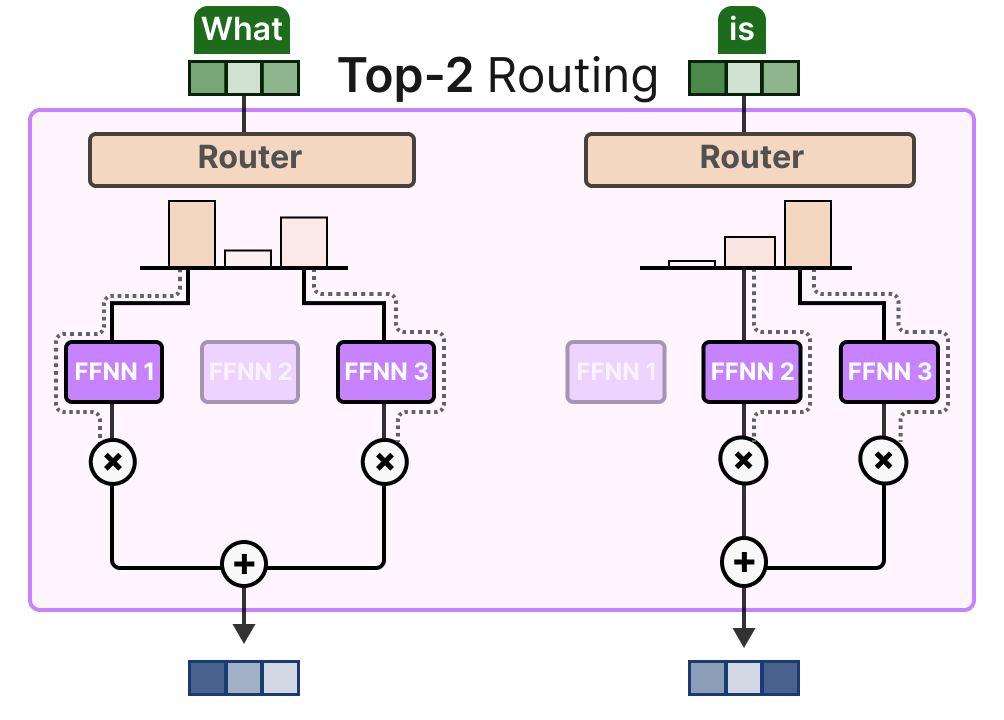
L’un de ses principaux avantages est de permettre d’évaluer et d’intégrer les contributions respectives des experts.

Perte auxiliaire Permalink

Pour obtenir une répartition plus homogène des experts pendant l’entraînement, la perte auxiliaire (également appelée perte d’équilibrage de la charge) a été ajoutée à la perte standard du réseau.
Cela ajoute une contrainte qui oblige les experts à avoir la même importance.
La première composante de cette perte auxiliaire consiste à additionner les valeurs des routeurs pour chaque expert sur l’ensemble du batch :

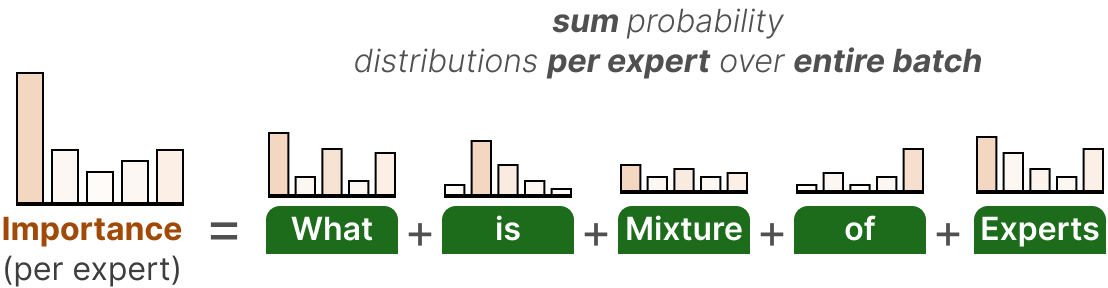
Cela nous donne les scores d’importance par expert qui représentent la probabilité qu’un expert donné soit choisi indépendamment de l’entrée.
Nous pouvons les utiliser pour calculer le coefficient de variation (CV), qui nous indique à quel point les scores d’importance sont différents d’un expert à l’autre :
Coefficient de variation(CV) = écart-type (σ) / moyenne (μ)

Par exemple, s’il y a beaucoup de différences dans les scores d’importance, le CV sera élevé :

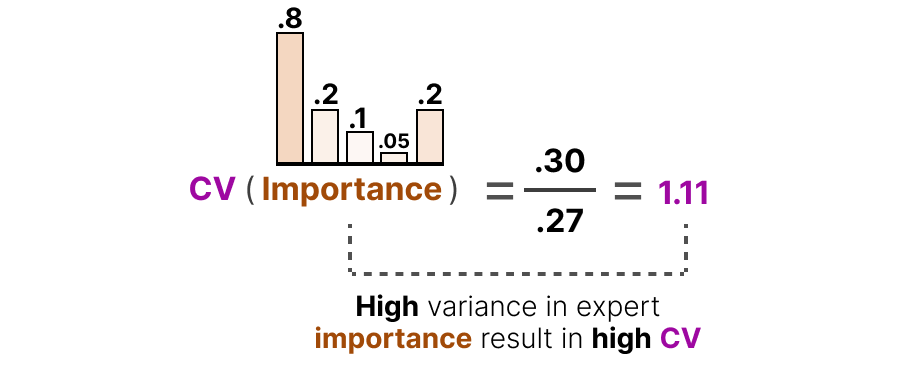
En revanche, si tous les experts ont des scores d’importance similaires, le CV sera faible (ce qui est notre objectif) :

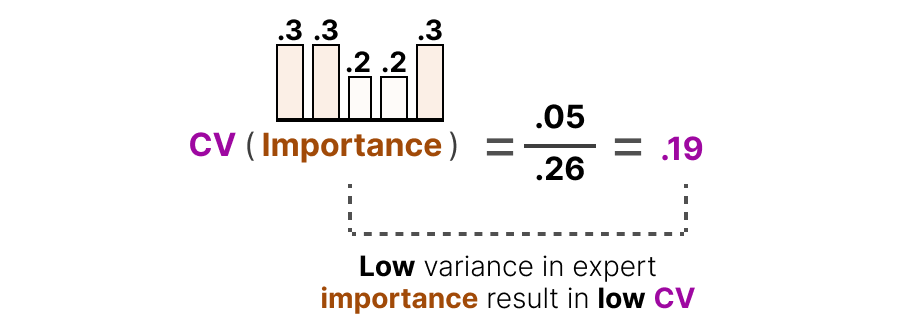
À l’aide de ce score CV, nous pouvons mettre à jour la perte auxiliaire pendant l’entraînement de manière à ce qu’elle vise à réduire autant que possible le score CV (en accordant ainsi la même importance à chaque expert) :

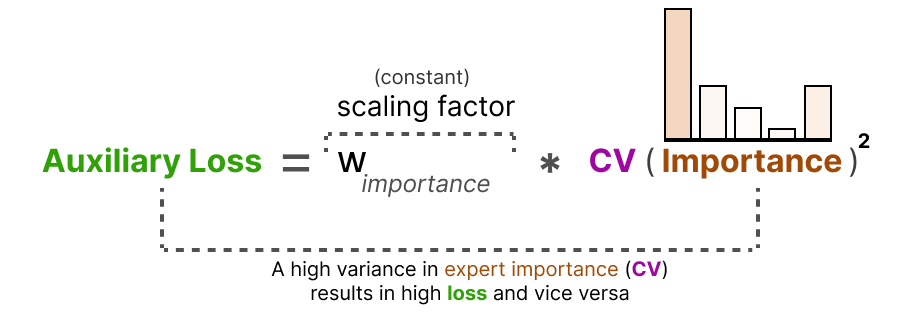
Enfin, la perte auxiliaire est ajoutée en tant que perte distincte à optimiser pendant la formation.

Capacité des experts Permalink

Le déséquilibre ne concerne pas seulement les experts sélectionnés, mais aussi les distributions des tokens envoyés à l’expert.
Par exemple, si les tokens d’entrée sont envoyés de manière disproportionnée à un expert plutôt qu’à un autre, cela peut également entraîner un sousentraînement :

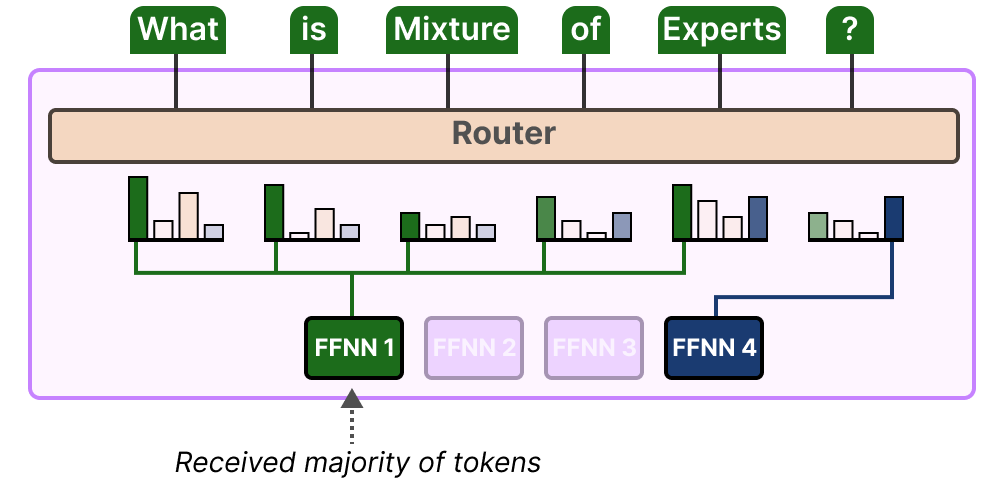
Ici, il ne s’agit pas seulement de savoir quels experts sont utilisés, mais aussi dans quelle mesure ils le sont.
Une solution à ce problème consiste à limiter la quantité de tokens qu’un expert donné peut traiter, autrement dit la capacité de l’expert (LEPIKHIN et al. (2020)). Lorsqu’un expert a atteint sa capacité, les tokens restants sont envoyés à l’expert suivant :

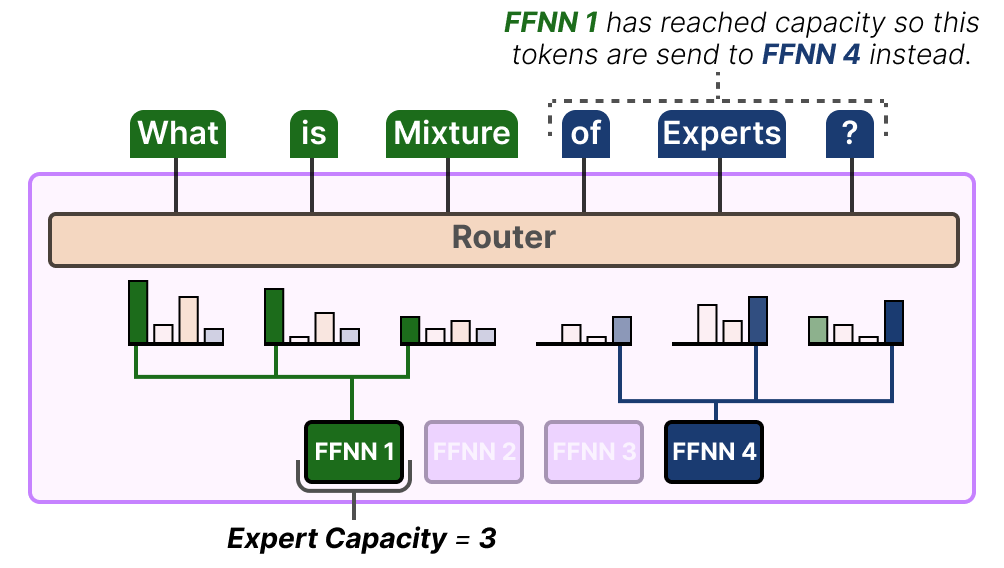
Si les deux experts ont atteint leur capacité, le token n’est traité par aucun expert et est envoyé à la couche suivante. C’est ce que l’on appelle le débordement de token (token overflow).

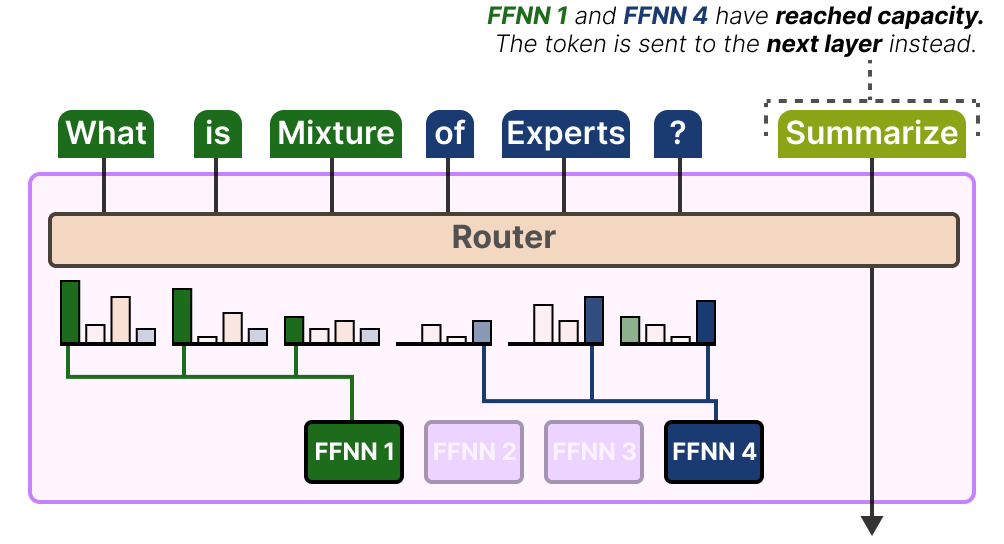
Simplifier le MoE avec Switch Transformer Permalink

L’un des premiers modèles de MoE basés sur un transformer ayant traité les problèmes d’instabilité durant l’entraînement (tels que l’équilibrage de la charge) est le Switch Transformer de FEDUS, ZOPH et SHAZZER (2021). Il simplifie une grande partie de l’architecture et de l’entraînement tout en augmentant la stabilité de ce dernier.

La couche de commutation (Switching Layer) Permalink

Le Switch Transformer est un modèle T5 (encodeur-décodeur) qui remplace la couche FFNN traditionnelle par une couche de commutation. Cette couche est une couche MoE éparse qui sélectionne un seul expert pour chaque token (routage top-$1$).

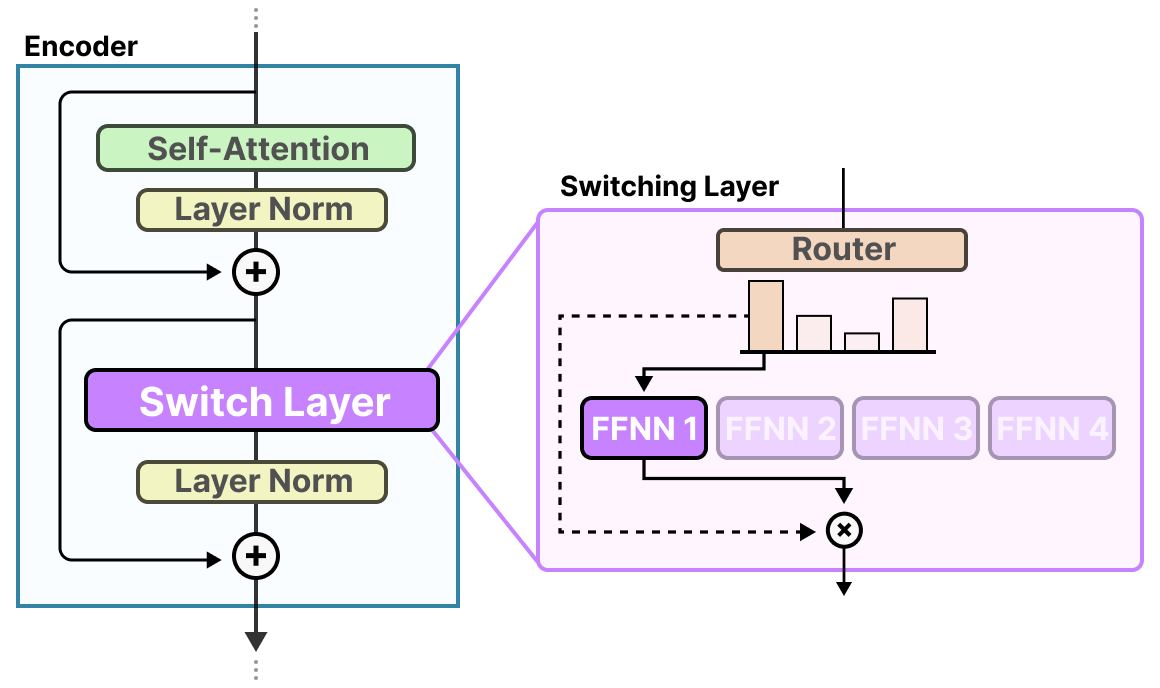
Le routeur ne fait aucun effort particulier pour calculer quel expert choisir et prend la softmax de l’entrée multipliée par les poids de l’expert (comme nous l’avons fait précédemment).

Cette architecture (routage top-$1$) suppose qu’un seul expert est nécessaire pour que le routeur apprenne comment acheminer l’entrée. Cela contraste avec ce que nous avons vu précédemment où nous avons supposé que les tokens devaient être acheminés vers plusieurs experts (routage top-$k$) pour apprendre le comportement de routage.

Facteur de capacité Permalink

Le facteur de capacité est une valeur importante car il détermine le nombre de tokens qu’un expert peut traiter. Le Switch Transformer va plus loin en introduisant un facteur de capacité qui influe directement sur la capacité de l’expert :
capacité de l’expert = (tokens par batch/nombre d’experts) * facteur de capacité

Les composantes de la capacité de l’expert sont simples :

Si nous augmentons le facteur de capacité, chaque expert pourra traiter davantage de tokens.

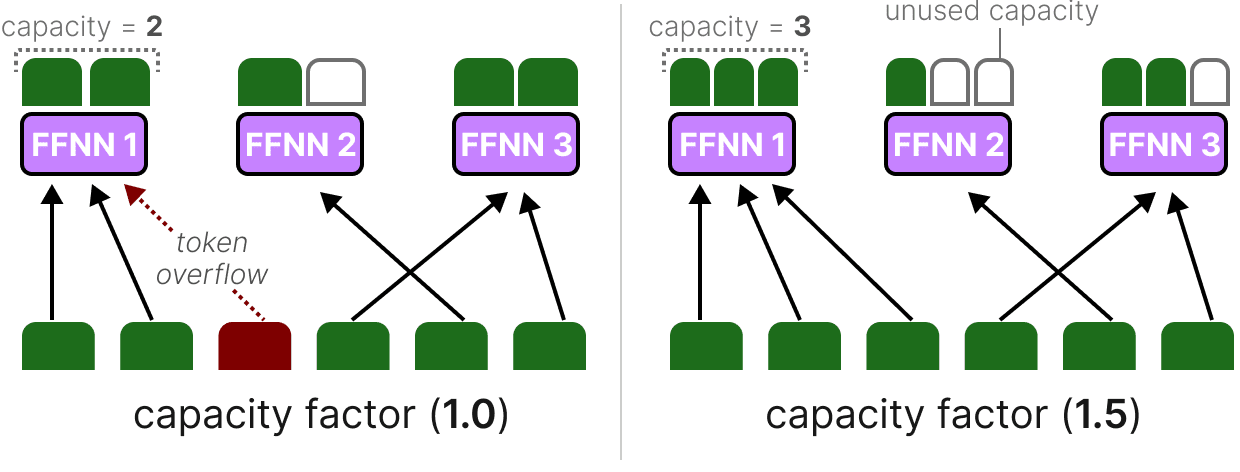
Cependant, si le facteur de capacité est trop élevé, nous gaspillons des ressources de calcul. À l’inverse, si le facteur de capacité est trop faible, les performances du modèle chuteront en raison du débordement des tokens.

Perte auxiliaire Permalink

Pour éviter de laisser tomber des tokens, une version simplifiée de la perte auxiliaire a été introduite.
Au lieu de calculer la variation du coefficient, cette perte pondère la fraction de tokens distribués par rapport à la fraction de probabilité de routage par expert :

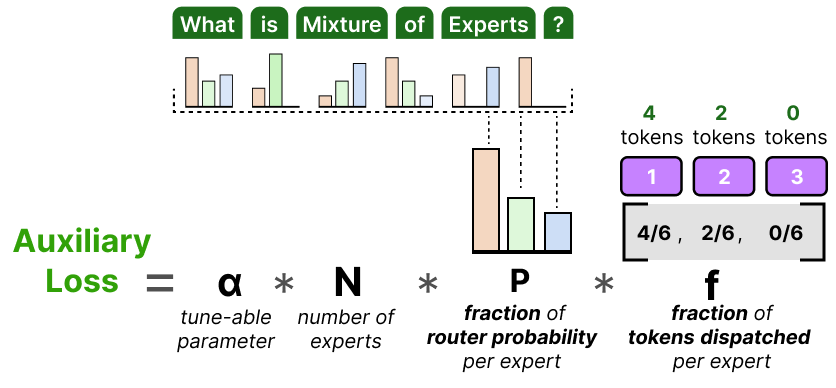
Puisque l’objectif est d’obtenir un routage uniforme des tokens parmi les $N$ experts, nous voulons que les vecteurs $P$ et $f$ aient des valeurs de $1/N$.
$α$ est un hyperparamètre que nous pouvons utiliser pour finetuner l’importance de cette perte pendant l’entraînement.
Des valeurs trop élevées prendront le pas sur la fonction de perte primaire et des valeurs trop faibles n’auront que peu d’effet sur l’équilibrage de la charge.

Mélange d’experts dans les modèles de visionPermalink

Le mélange d’expert n’est pas une technique réservée aux modèles de langage. En effet, les modèles de vision, tels que les Vision-Transformer (ViT par DOSOVITSKIY, BEYER, KOLESNIKOV, WEISSENBORN, ZHAI, HOULSBY et al. (2020)), s’appuyant sur des architectures basées sur des transformers peuvent également utiliser le MoE.
Pour rappel, le ViT est une architecture qui divise les images en patchs qui sont traitées de la même manière que les tokens.

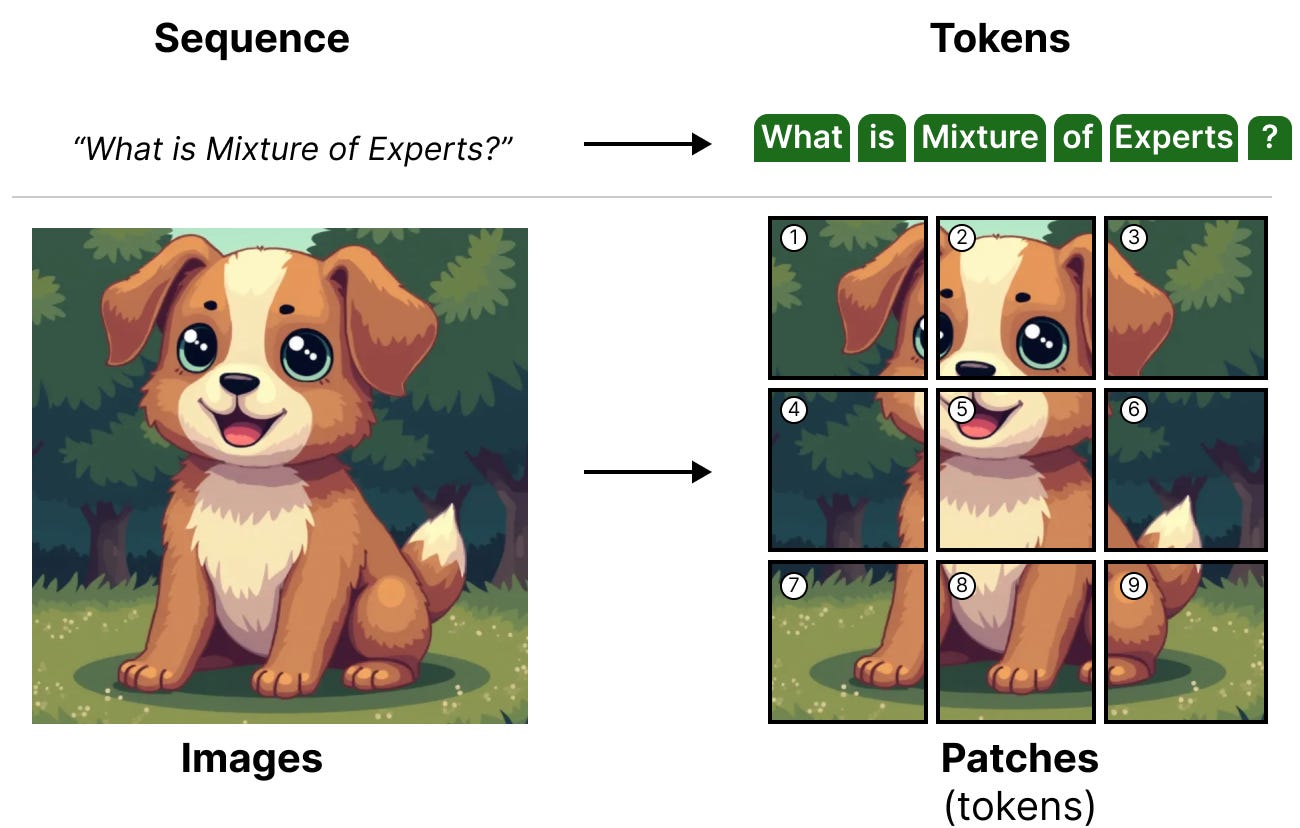
Ces patchs (ou tokens) sont ensuite projetés dans des enchâssements (avec des enchâssements positionnels) avant d’être introduits dans un encodeur classique :

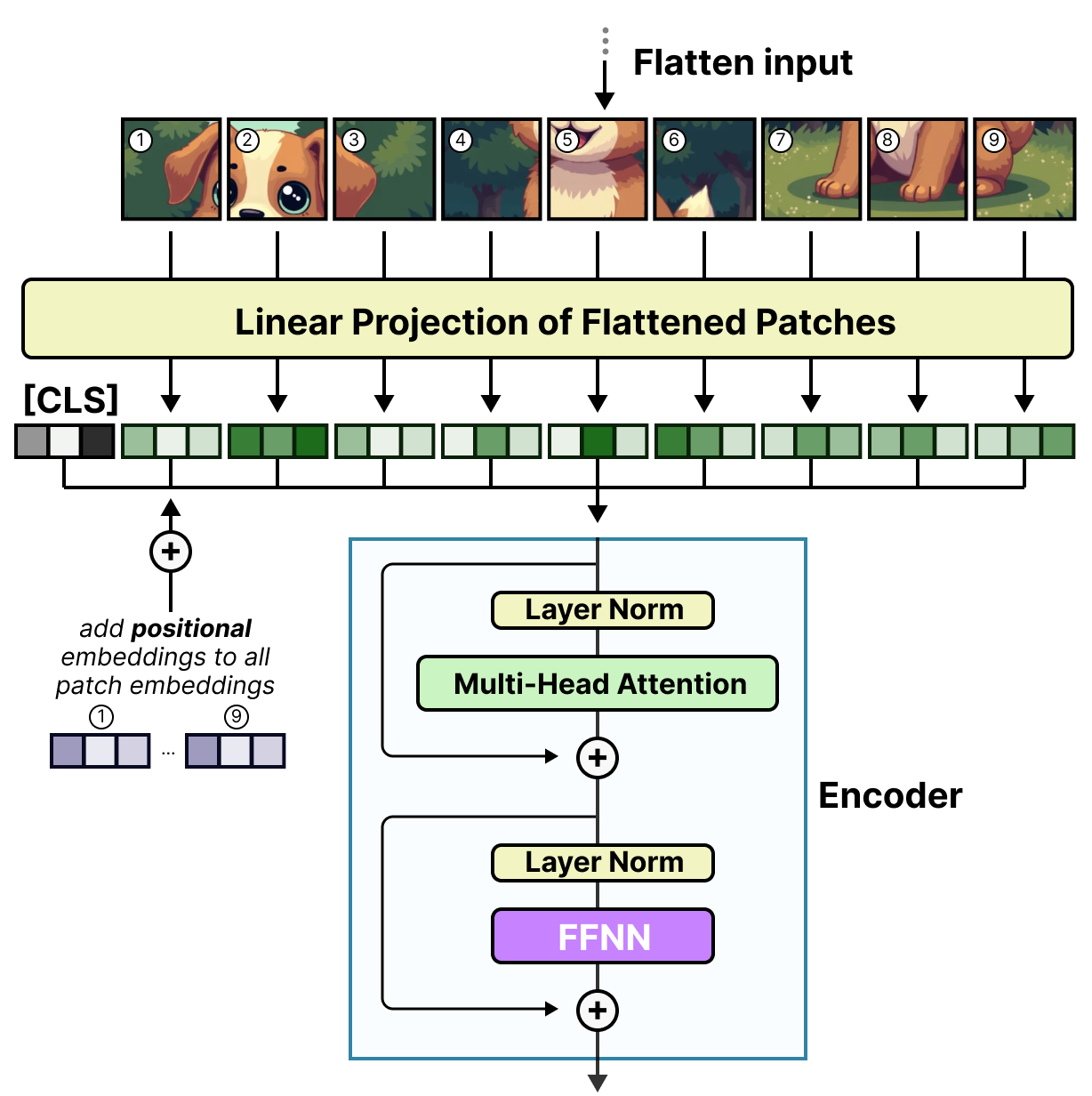
Au moment où ces patchs entrent dans l’encodeur, ils sont traités comme des tokens, ce qui permet à cette architecture de s’adapter parfaitement à un MoE.

Vision-MoE Permalink

Vision-MoE (V-MoE) par RIQUELME, PUIGCERVER, MUSTAFA et al. (2021) est l’une des premières implémentations de MoE dans un modèle d’image. Elle prend le ViT comme nous l’avons vu précédemment et remplace le FFNN dense dans l’encodeur par un MoE épars.

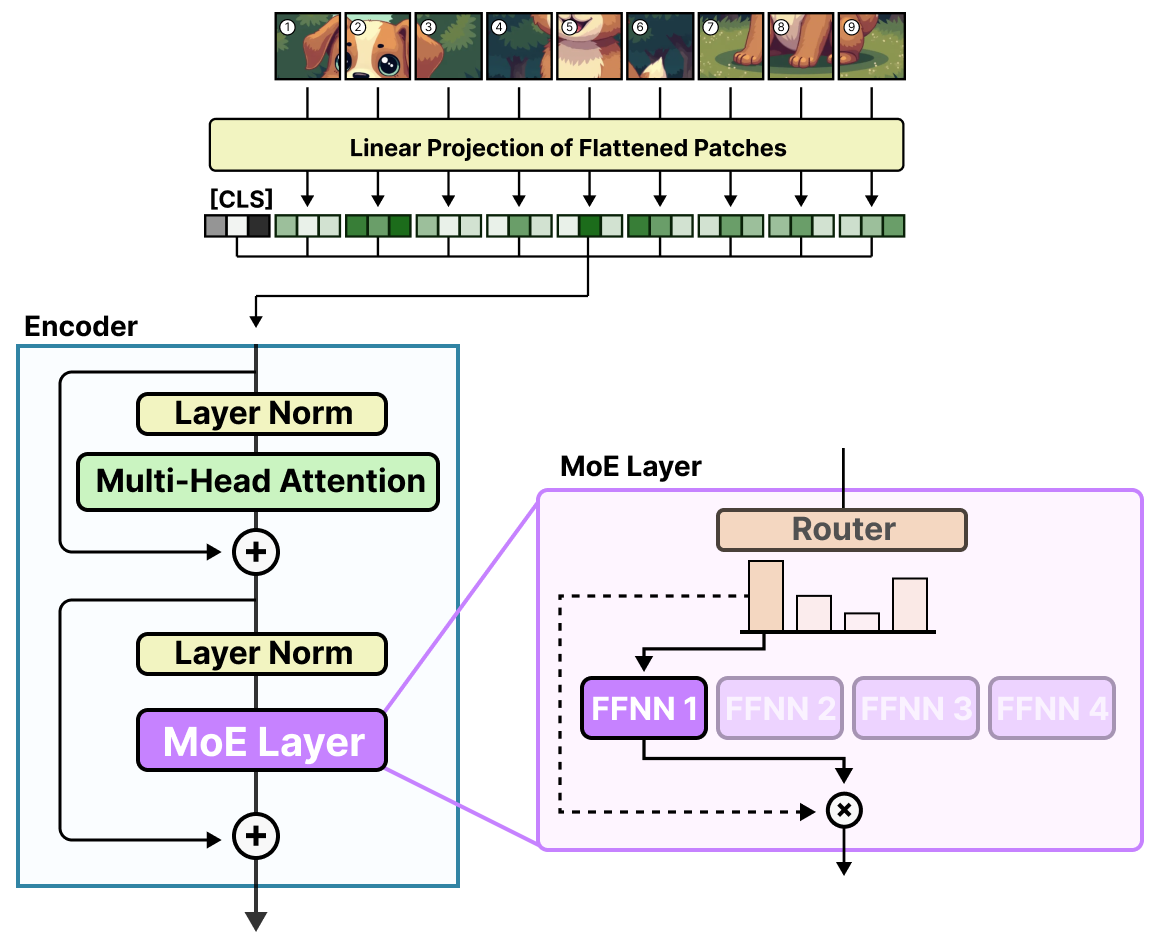
Cela permet aux ViT, généralement plus petits que les modèles de langage, de passer massivement à l’échelle via l’ajout d’experts.
Une petite capacité d’expertise prédéfinie a été utilisée pour chaque expert afin de réduire les contraintes matérielles, car les images comportent généralement de nombreux patchs. Toutefois, une faible capacité a tendance à entraîner l’abandon de correctifs (ce qui s’apparente à un débordement de tokens).

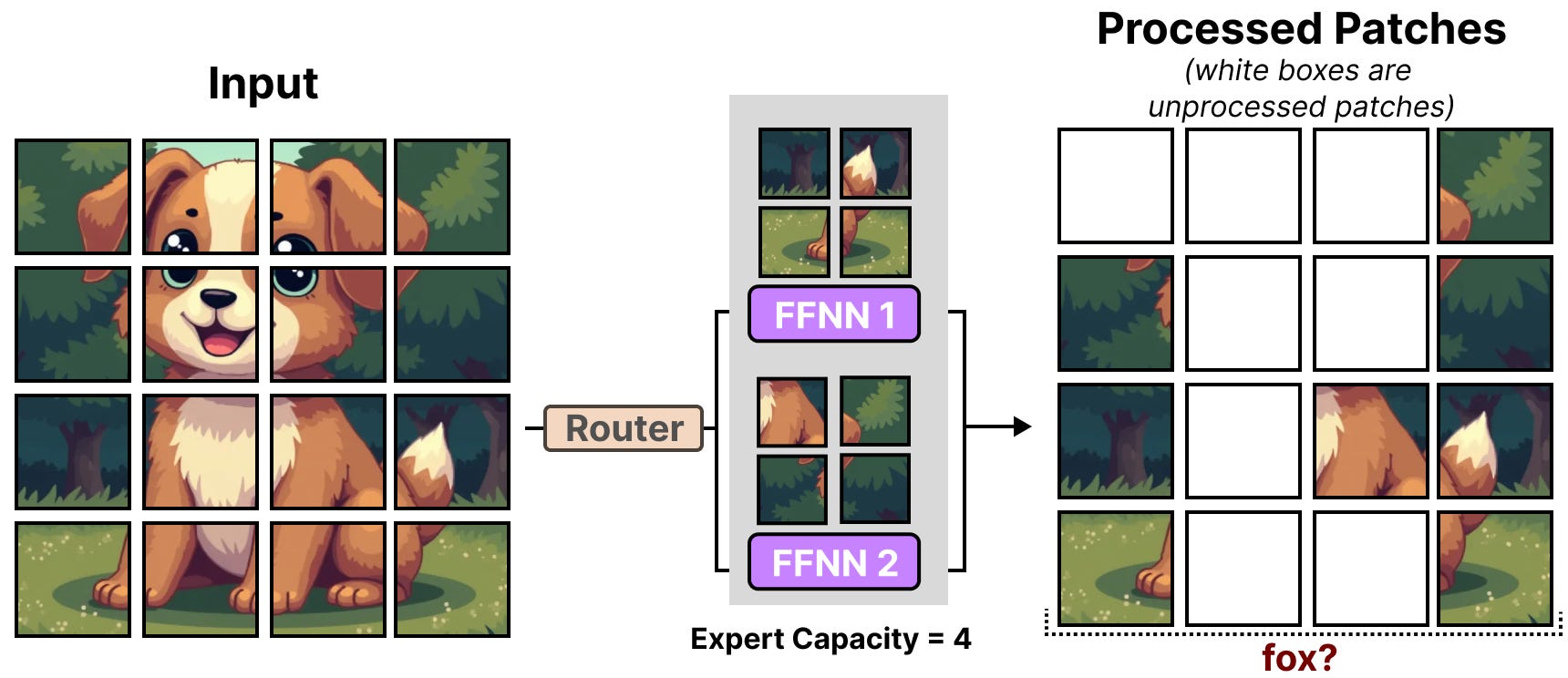
Pour maintenir la capacité basse, le réseau attribue des scores d’importance aux patchs et les traite en premier, ainsi les patchs débordants sont généralement moins importants. C’est ce qu’on appelle le routage prioritaire par batchs.

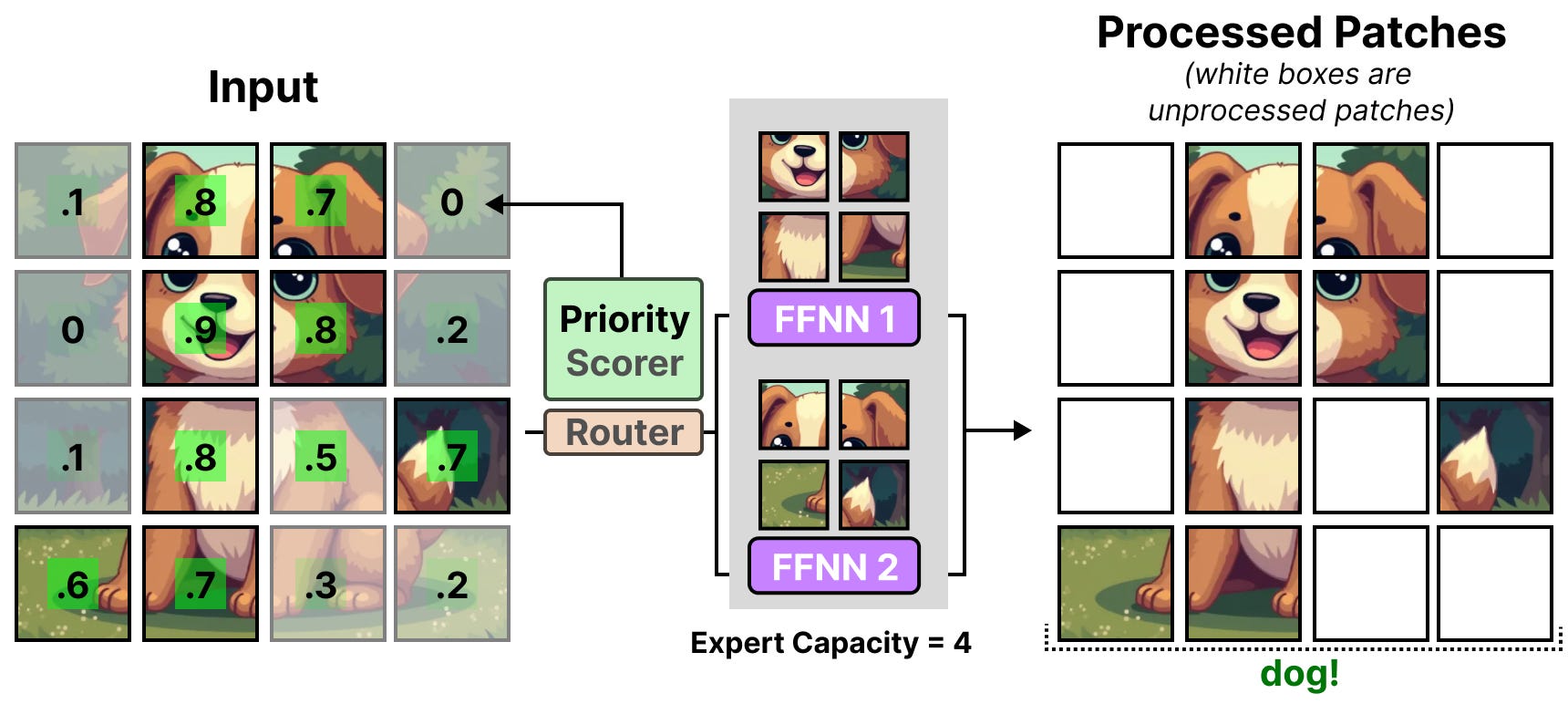
Par conséquent, les patchs importants devraient toujours être acheminés si le pourcentage de tokens diminue.

Le routage prioritaire permet de traiter moins de patchs en se concentrant sur les plus importants.

De V-MoE à Soft-MoE Permalink

Dans V-MoE, le système d’évaluation des priorités permet de différencier les patchs plus ou moins importants. Cependant, ils sont attribués à chaque expert et les informations contenues dans ceux non traités sont perdues.
L’objectif de Soft-MoE de PUIGCERVER, RIQUELME et al. (2023) est de passer d’une affectation discrète à une affectation souple en mélangeant les patchs.
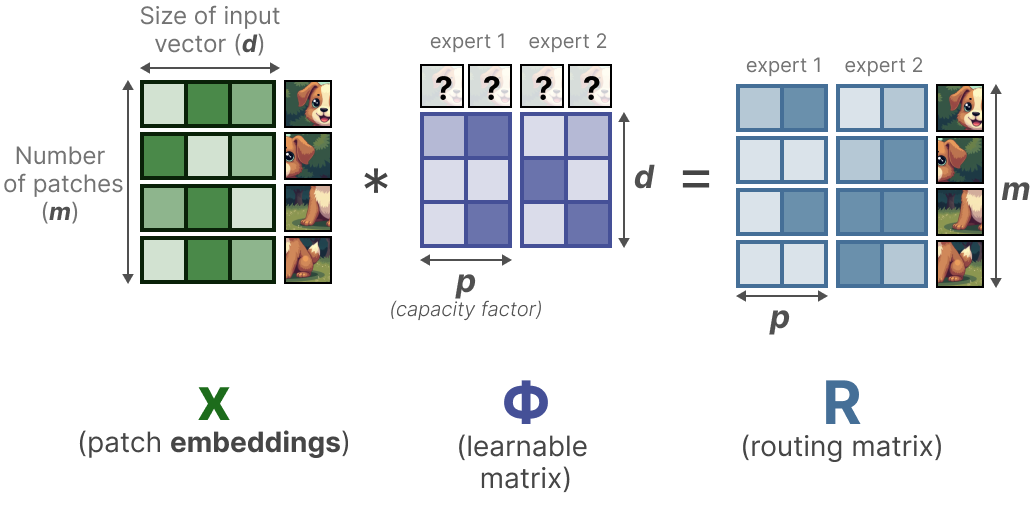
Dans un premier temps, nous multiplions l’entrée x (les patchs d’enchâssements) par une matrice apprenable Φ. Ceci nous donne des informations pour le routeur pour indiquer dans quelle mesure un certain token est lié à un expert donné.

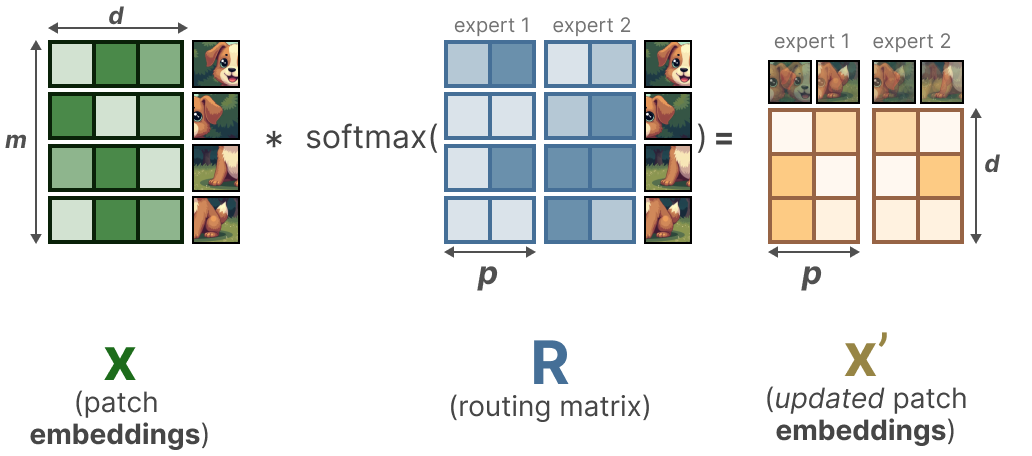
En prenant ensuite la softmax (sur les colonnes) de la matrice d’information du routeur R, nous mettons à jour les enchâssements de chaque patch.

La mise à jour des enchâssements des patchs est essentiellement la moyenne pondérée de tous les enchâssements des patchs.

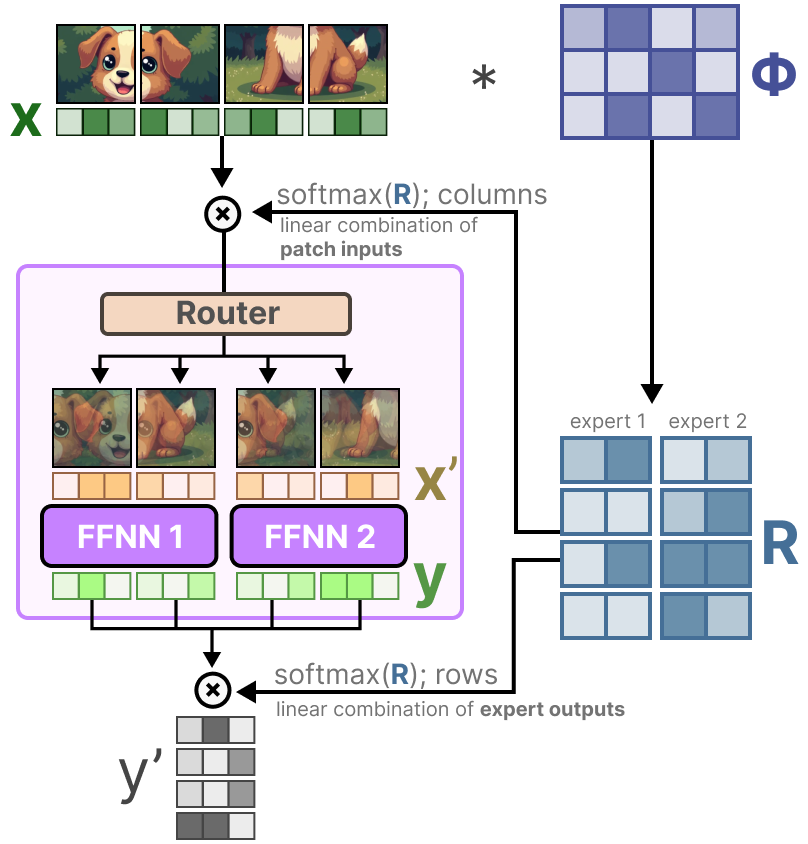
Visuellement, c’est comme si tous les patchs étaient mélangés. Ces patchs combinés sont ensuite envoyés à chaque expert. Après avoir généré la sortie, ils sont à nouveau multipliés par la matrice de routage R.

La matrice de routage affecte l’entrée au niveau du token et la sortie au niveau de l’expert.
En conséquence, nous obtenons des patchs/tokens « souples » qui sont traités au lieu d’une entrée discrète.

Mixtral 8x7B : paramètres actifs vs. Paramètres éparsPermalink

Une grande partie de l’intérêt d’un MoE réside dans ses impératifs en matière de calcul. Étant donné que seul un sous-ensemble d’experts est utilisé à un moment donné, nous avons accès à plus de paramètres que nous n’en utilisons.
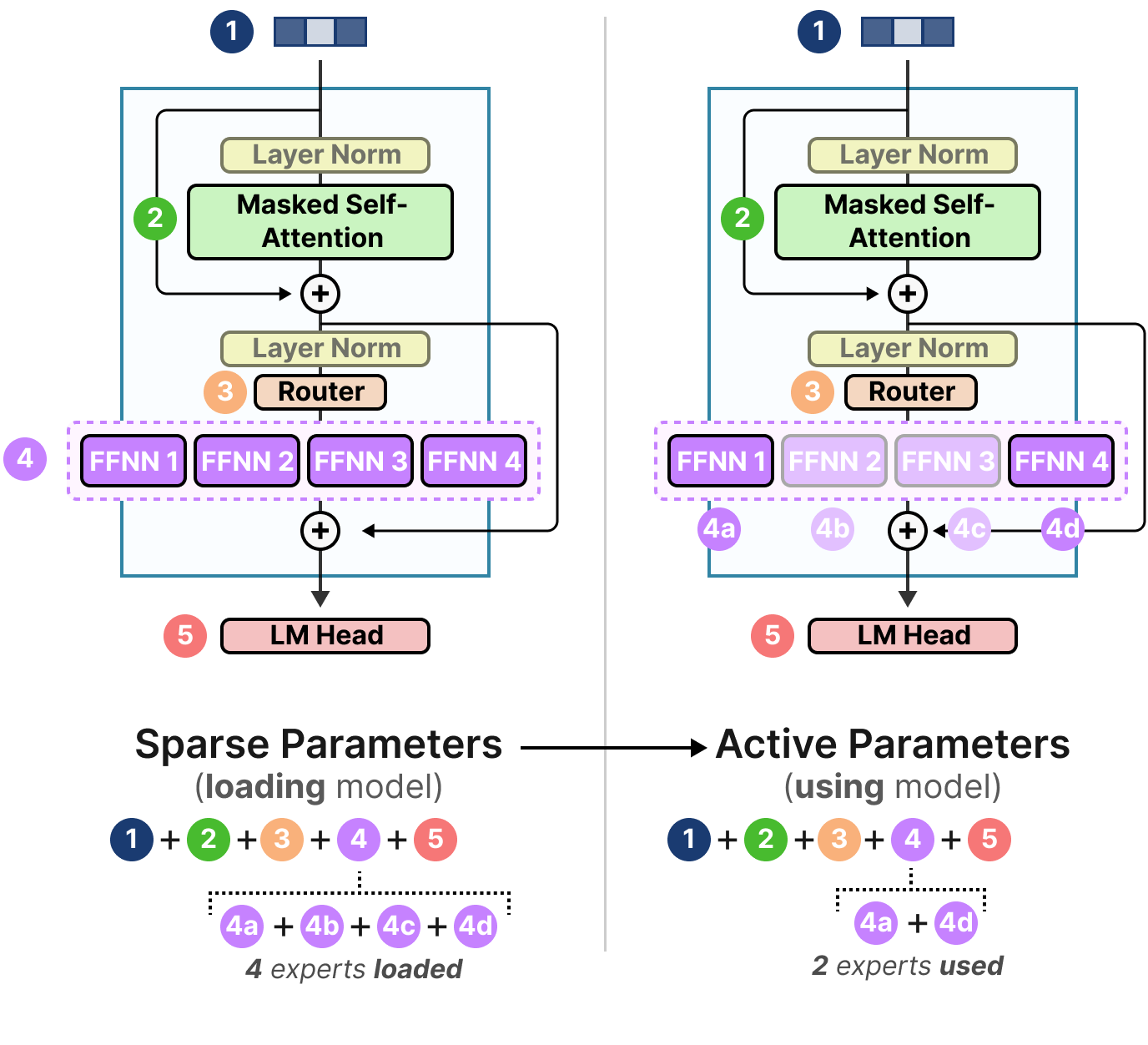
Bien qu’un MoE donné ait plus de paramètres à charger (paramètres épars), moins sont activés puisque nous n’utilisons que certains experts pendant l’inférence (paramètres actifs).

En d’autres termes, nous devons toujours charger l’ensemble du modèle (incluant tous les experts) sur l’appareil (paramètres épars), mais lorsque nous procédons à l’inférence, nous ne devons utiliser qu’un sous-ensemble (paramètres actifs). Les modèles avec MoE ont besoin de plus de VRAM pour charger tous les experts, mais s’exécutent plus rapidement pendant l’inférence.
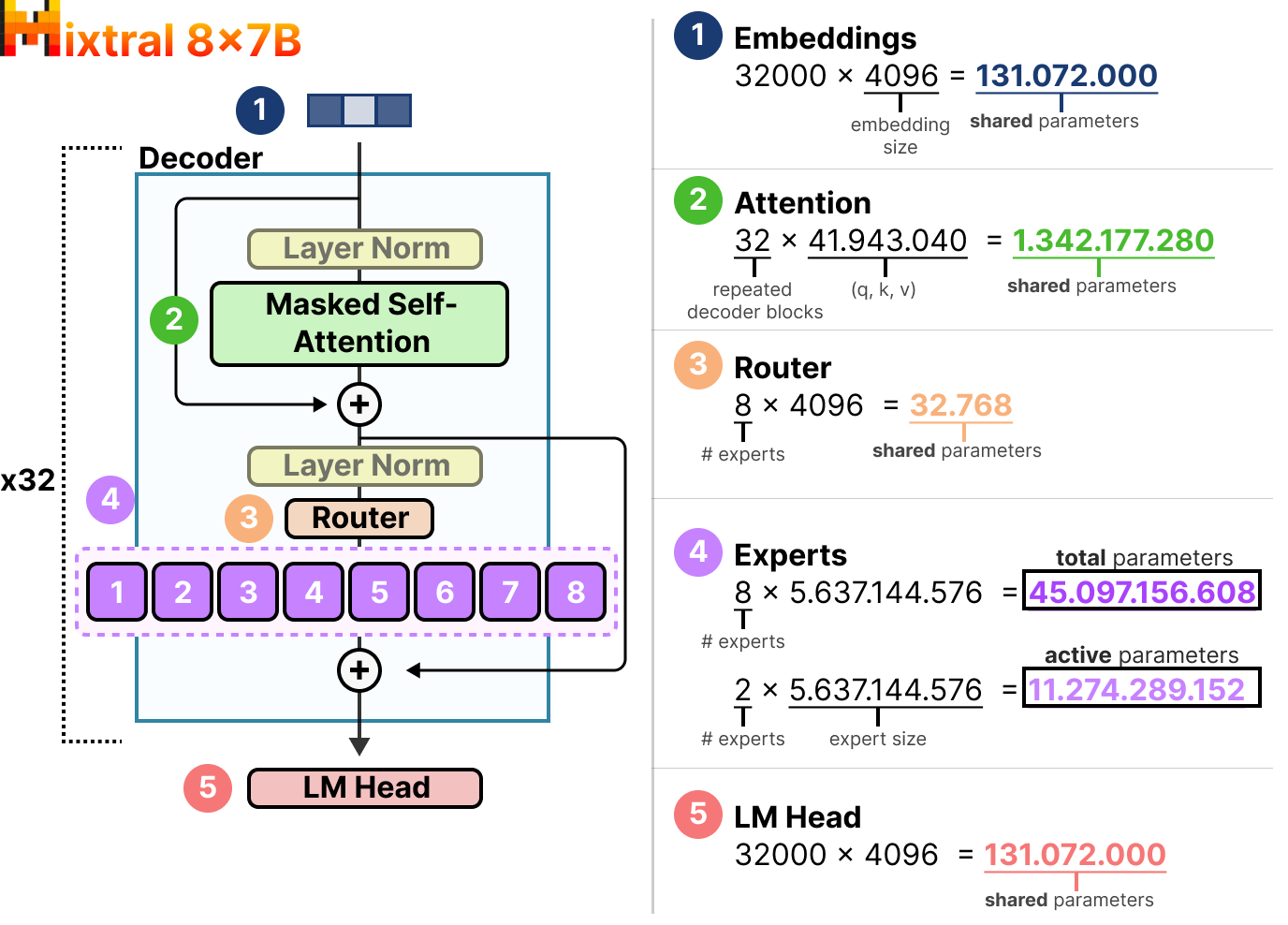
Comme exemple, examinons le nombre de paramètres épars par rapport aux paramètres actifs du Mixtral 8x7B de Mistral (2024).

Nous pouvons constater que chaque expert a une taille de $5,6$Mds et non de $7$ (bien qu’il y ait $8$ experts).

Nous devrons charger $8$x$5,6$Mds ($46,7$Mds) de paramètres (ainsi que tous les paramètres partagés) mais nous n’utiliserons que $2$x$5,6$Mds ($12,8$Mds) paramètres pour l’inférence.

Conclusion Permalink

Ceci conclut notre voyage avec les mélanges d’experts ! En espérant que cet article vous a permis de mieux comprendre le potentiel de cette technique. Maintenant que presque tous les LLM contiennent au moins une variante de MoE, il semble que cette technique soit là pour rester.
J’espère que cette introduction a été accessible. Si vous souhaitez aller plus loin sur ce sujet, je vous suggère les ressources suivantes :
• Ce papier par FEDUS, DEAN et ZOPH (2022) ainsi que celui-ci par CAI, JIANG, WANG et al. (2024) offrent une excellente vue d’ensemble des dernières innovations concernant les MoE.
• Le papier de ZHOU et al. (2022) sur le choix du routage.
• Un excellent article de blog par Cameron R. WOLFE qui passe en revue quelques-uns des principaux documents (et leurs conclusions).
• Un article de blog par Bruno MAGALHAES retraçant la chronologie de MoE.

Références Permalink

• A Visual Guide to Mixture of Experts (MoE) de Maarten GROOTENDORST (2024)
• ST-MoE: Designing Stable and Transferable Sparse Expert Models de Barret ZOPH, Irwan BELLO, Sameer KUMAR, Nan DU, Yanping HUANG, Jeff DEAN, Noam SHAZEER et William FEDUS (2022)
• Mixtral of Experts de Mistral (2024)
• Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer par Noam SHAZEER, Azalia MIRHOSEINI, Krzysztof MAZIARZ Andy DAVIS, Quoc LE, Geoffrey HINTON et Jeff DEAN (2017)
• GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding de Dmitry LEPIKHIN, HyoukJoong LEE, Yuanzhong XU, Dehao CHEN, Orhan FIRAT, Yanping HUANG, Maxim KRIKUN, Noam SHAZEER et Zhifeng CHEN (2020)
• Switch Transformer: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity de William FEDUS, Barret ZOPH et Noam SHAZZER (2021)
• An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale par Alexey DOSOVITSKIY, Lucas BEYER, Alexander KOLESNIKOV, Dirk WEISSENBORN, Xiaohua ZHAI, Thomas UNTERTHINER, Mostafa DEHGHANI, Matthias MINDERER, Georg HEIGOLD, Sylvain GELLY, Jakob USKOREIT et Neil HOULSBY (2020)
• Scaling Vision with Sparse Mixture of Experts (V-MoE) par Carlos RIQUELME, Joan PUIGCERVER, Basil MUSTAFA, Maxim NEUMANN, Rodolphe JENATTON, André SUSANO PINTO, Daniel KEYSERS et Neil HOULSBY (2021)
• From Sparse to Soft Mixtures of Experts de Joan PUIGCERVER, Carlos RIQUELME, Basil MUSTAFA et Neil HOULSBY (2023)
• A Review of Sparse Expert Models in Deep Learning par William FEDUS, Jeff DEAN et Barret ZOPH (2022)
• A Survey on Mixture of Experts par Weilin CAI, Juyong JIANG, Fan WANG, Jing TANG, Sunghun KIM et Jiayi HUANG (2024)
• Mixture-of-Experts with Expert Choice Routing de Yanqi ZHOU, Tao LEI, Hanxiao LIU, Nan DU, Yanping HUANG, Vincent ZHAO, Andrew DAI, Zhifeng CHEN, Quoc LE et James LAUDON (2022)

Citation Permalink

@inproceedings{MoE_blog_post,
author = {Loïck BOURDOIS},
title = {Un guide visuel sur le mélange d'experts (MoE)},
year = {2025},
url = {https://lbourdois.github.io/blog/MoE/}
}