Introduction
Dans l’article précédent, nous avons défini ce qu’est un State Space Model (SSM) à l’aide d’un système en temps continu. Nous l’avons discrétisé pour faire apparaître sa vue récurrente puis convolutive. L’intérêt ici est de pouvoir entraîner le modèle de manière convolutive puis de réaliser l’inférence de manière récurrente sur de très longues séquences.
| Figure 1 : Image provenant de l’article de blog « Structured State Spaces: Combining Continuous-Time, Recurrent, and Convolutional Models » d’Albert GU et al. (2022) |
Cette vision a été introduite par Albert GU dans ses papiers LSSL et S4 parus en 2021. Le S4 étant l’équivalent du « Attention is all you need » pour les transformers.
Dans le présent article, nous allons passer en revue la littérature des SSM parus durant l’année 2022. Ceux apparus en 2023 seront listés dans le prochain article.
L’objectif est de montrer les différentes évolutions de ces types de modèles au cours des mois, tout en restant synthétique (i.e. je ne vais pas rentrer dans tous les détails des papiers listés). Lors de cette année 2022, les différentes avancées se sont focalisées à appliquer des algorithmes de discrétisations différents, tout en remplaçant la matrice HiPPO par une plus simple.
Modèles théoriques
Dans cette section, nous allons passer en revue les travaux théoriques des propositions d’amélioration de l’architecture du S4 vont être passés en revue. Nous aborderons ensuite dans une section différente, des applications concrètes sur différentes tâches (audio, vision, etc.).
S4 V2
Le 4 mars 2022, les auteurs du S4 ont actualisé leur papier afin d’y intégrer une section sur l’importance de la matrice HiPPO (cf. la section 4.4 de la version la plus récente du papier).
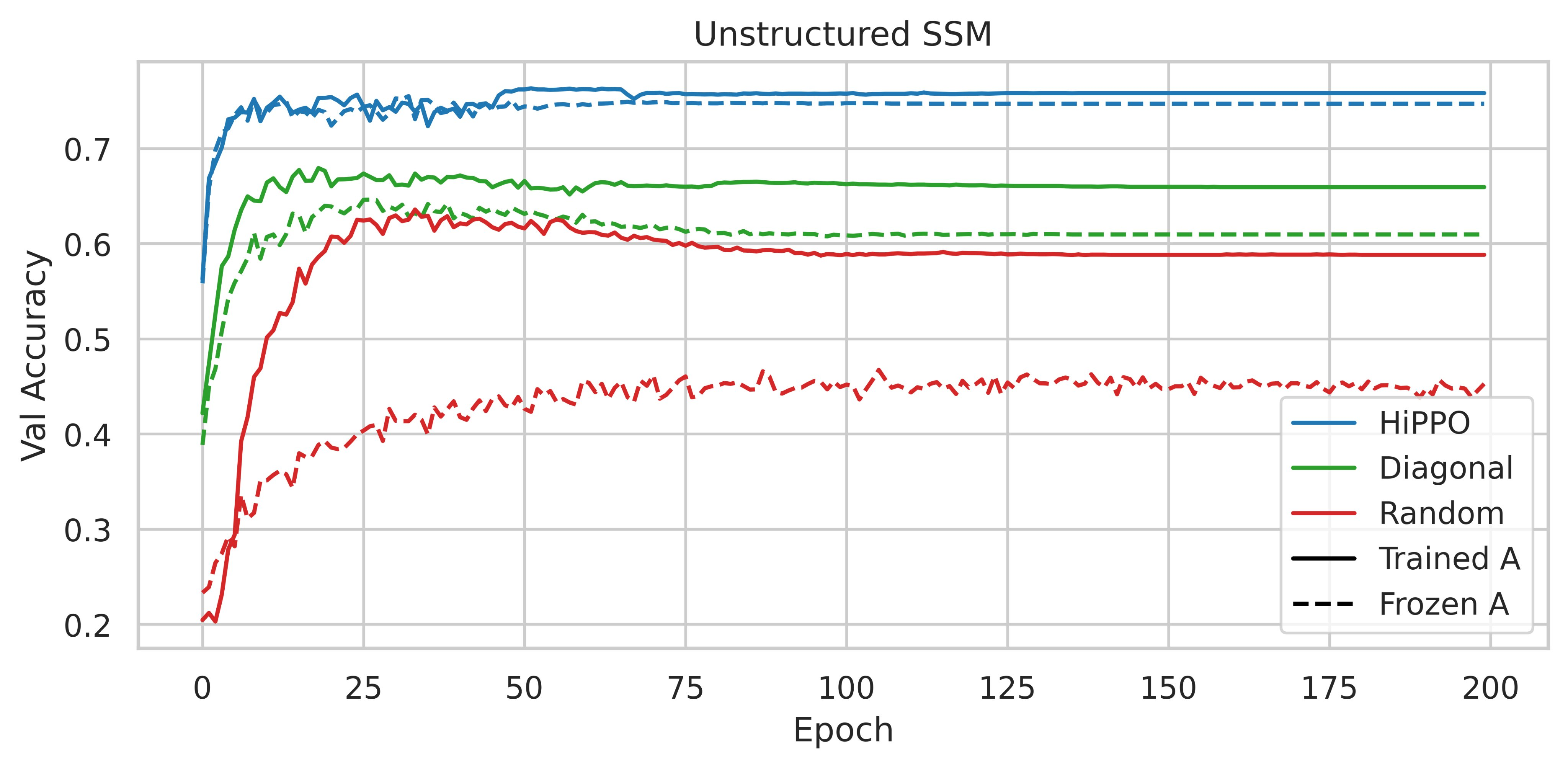
Pour résumer, elle consiste à rapporter les résultats observés à la suite de la réalisation d’ablations sur le jeu de données séquentielles CIFAR-10. Au lieu d’utiliser un SSM avec la matrice HiPPO, les auteurs ont essayé d’utiliser diverses paramétrisations comme une matrice dense aléatoire et une matrice diagonale aléatoire.
 |
|---|
| Figure 2 : Accuracy sur l’échantillon de validation de CIFAR-10, tirée de la figure 3 du papier du S4 |
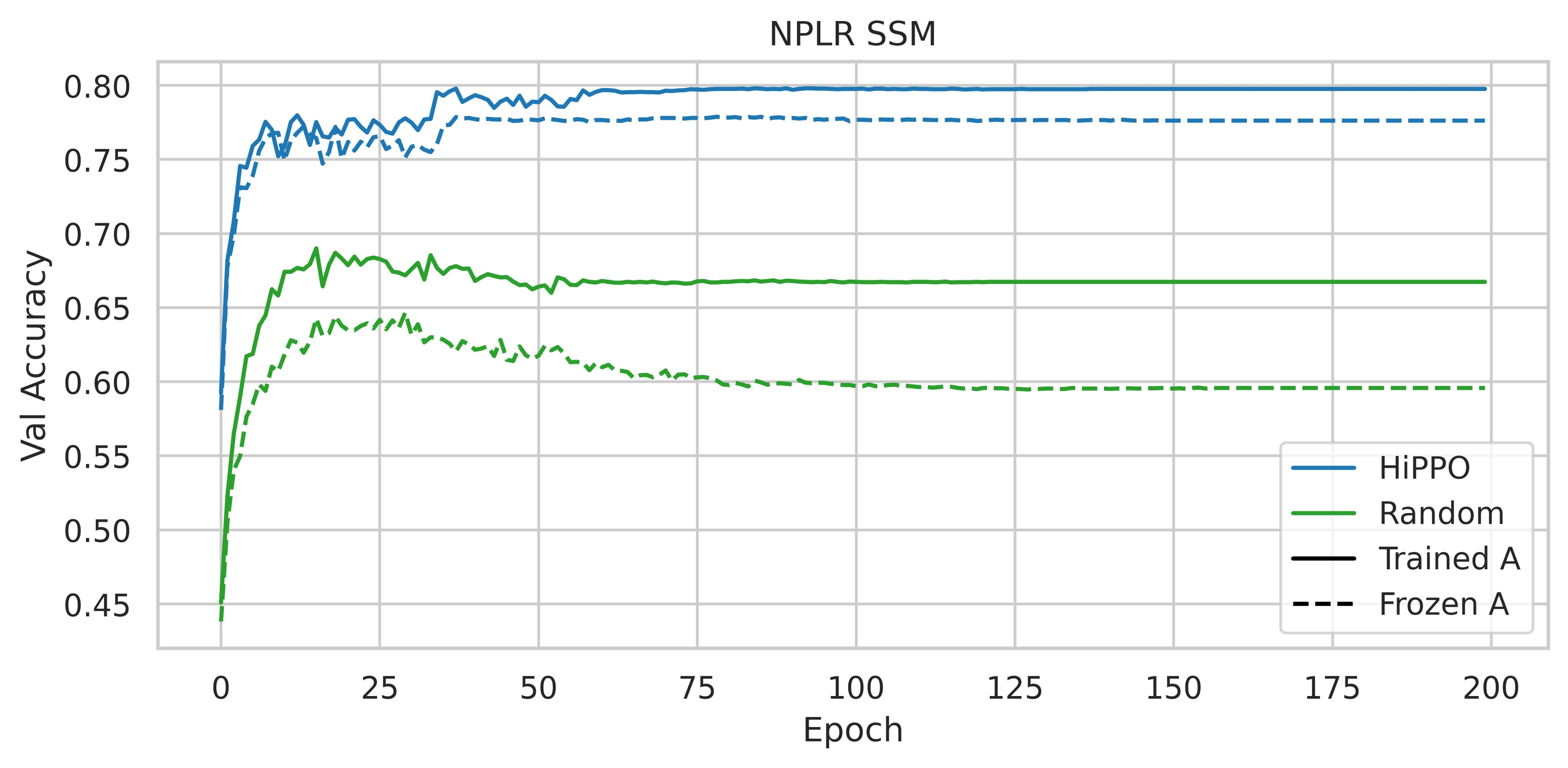
L’utilisation d’HiPPO se révèle donc importante, les performances obtenues sont-elles dues à ses qualités intrinsèques spécifiques ou bien n’importe quelle matrice normale à faible rang (NPLR pour Normal Plus Low-Rank) pourrait suffire ?
 |
|---|
| Figure 3 : Accuracy sur l’échantillon de validation de CIFAR-10 avec différentes initialisations et parameterisations, tirée de la figure 4 du papier du S4 |
Initialiser une matrice NPLR avec HiPPO augmente considérablement les performances.
Ainsi, d’après ces expériences, la matrice HiPPO est primordiale afin d’obtenir un modèle performant.
Les auteurs du S4 ont approfondi leurs travaux qu’ils ont exposés le 24 juin 2022 dans l’article How to Train Your HiPPO. Il s’agit d’un papier extrêmement détaillé de plus de 39 pages.
Dans cet article, les auteurs se concentrent sur une interprétation plus intuitive des SSM en tant que modèle convolutif où le noyau de convolution est une combinaison linéaire de fonctions de base particulières, ce qui conduit à plusieurs généralisations et à de nouvelles méthodes.
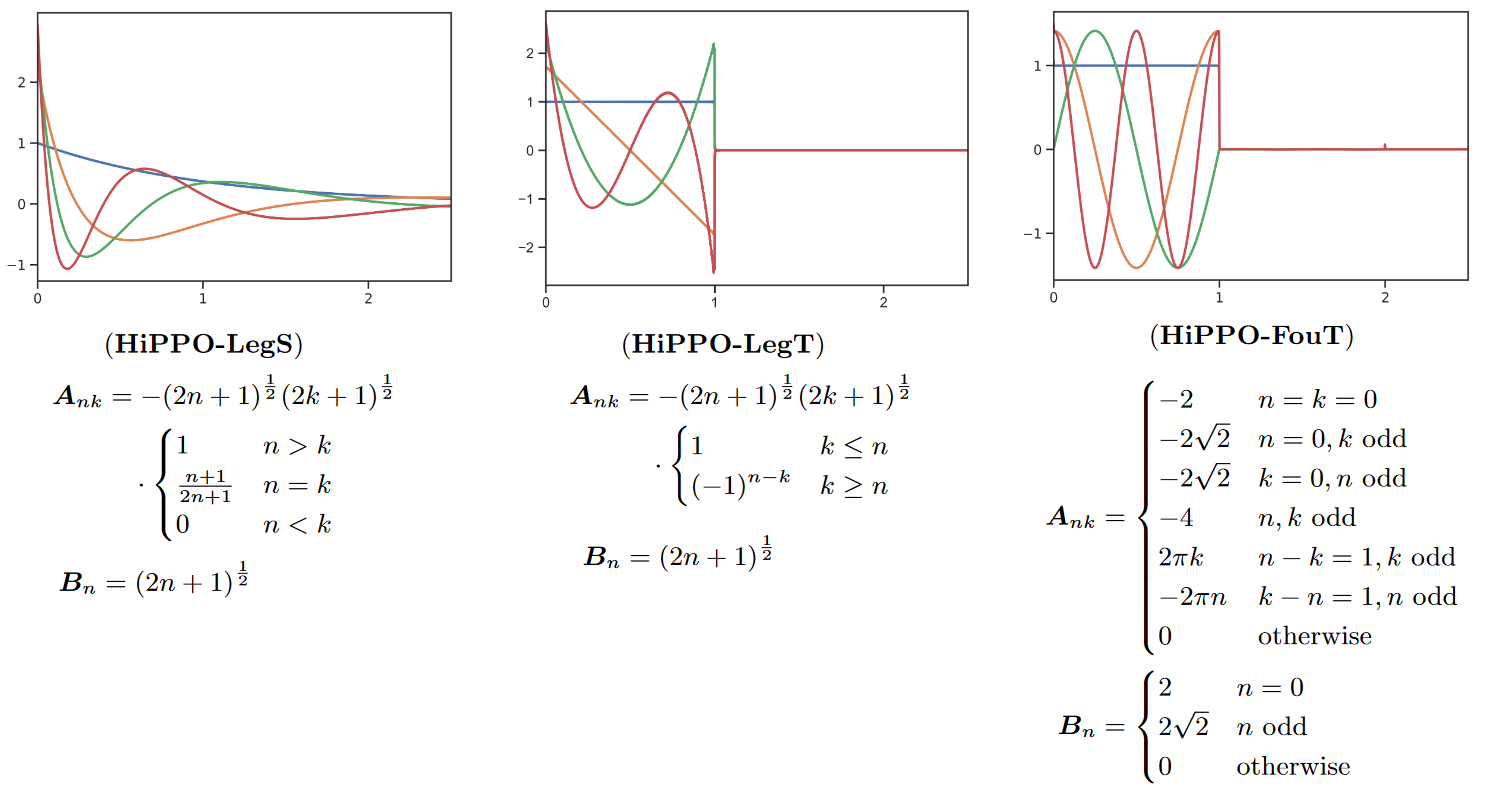
Ainsi, ils prouvent que la matrice \(\mathbf{A}\) du S4 produit des polynômes de Legendre à échelle exponentielle (LegS). Cela confère au système une meilleure capacité à modéliser les dépendances à long terme via des noyaux très lisses.
Les auteurs dérivent également un nouveau SSM qui produit des approximations de fonctions de Fourier tronquées (FouT). Cette méthode généralise les transformées de Fourier à court terme et les convolutions locales (c’est-à-dire un ConvNet standard). Ce SSM peut également coder des fonctions de pointe pour résoudre des tâches de mémorisation classiques.
A noter que c’est surtout HiPPO-FouT qui est introduit dans ce papier, HiPPO-LegS ayant été introduit dans le papier original d’HiPPO deux ans plus tôt. De même qu’HiPPO-LegT (polynômes de Legendre tronqués).
 |
|---|
| Figure 4 : Les différentes variantes d’HiPPO |
Les couleurs représentent les 4 premières fonctions de base \(K_n(t)\) (le noyau de convolution) pour chacune des méthodes (nous invitons le lecteur à regarder le tableau 1 du papier pour savoir à quoi équivaut \(K_n(t)\) pour chacune des méthodes).
De plus, les auteurs travaillent également sur le pas de temps \(∆\), qui indépendamment d’une notion de discrétisation peut être interprété simplement comme contrôlant la longueur des dépendances ou la largeur des noyaux du SSM. Les auteurs détaillent aussi comment choisir une bonne valeur de \(∆\) pour une tâche donnée.
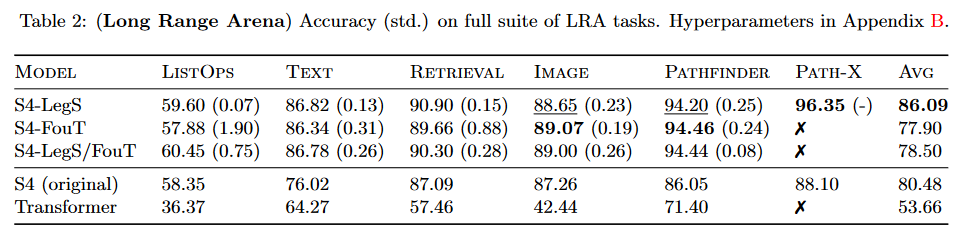
Les travaux menés permettent d’améliorer les résultats du S4 de plus de 5,5 points sur le benchmark LRA de TAY, DEHGHANI et al. (2020) :
 |
|---|
| Figure 5 : Résultats du S4 v2 sur le benchmark |
Le modèle résultant de ce papier est généralement appelé « S4 V2 » ou « S4 updated » dans la littérature à opposer au « S4 original » ou « S4 V1 ».
Le DSS : Diagonal State Spaces
Le 27 mars 2022, Ankit GUPTA introduit dans son papier Diagonal State Spaces are as Effective as Structured State Spaces les Diagonal State Spaces (DSS).
Il semble que suite à ce papier, Albert GU et lui se soient mis à travailler ensemble d’une part sur une version actualisée de ce papier (GU apparaissant par la suite comme co-auteur dans les v2 et v3 de l’article) et d’autre part dans le cadre du S4D (voir section suivante).
La principale chose à retenir est que cette approche est sensiblement plus simple que le S4. En effet, le DSS repose sur des matrices d’état diagonales (donc sans la correction de rang faible du S4, i.e. sans la matrice HiPPO) qui, si sont initialisées de manière appropriée, fonctionnent mieux que le S4 original. L’usage d’une matrice diagonale à la place de la matrice HiPPO pour \(\mathbf{A}\) est depuis devenu une norme.
Arrêtons-nous néanmoins sur les quelques complexités/limites que contiennent ce papier. En les listant nous pourrons comprendre les apports des méthodes suivantes qui visent à simplifier davantage les choses.
1. La discrétisation
Le DSS utilise le même système d’équations différentielles que le S4 :
Cependant il utilise une discrétisation différente afin d’aboutir aux vues convolutives et récurrentes, à savoir la discrétisation zero-order hold (ZOH) ou bloqueur d’ordre zéro en français, au lieu de la discrétisation bilinéaire, qui suppose que le signal échantilloné est constant entre chaque point d’échantillonnage.
Ci-dessous un tableau comparatif des valeurs de \(\mathbf{A}\), \(\mathbf{B}\) et \(\mathbf{C}\) pour chacune des deux discrétisations dans la vue récurrente, ainsi que l’expression du noyau de convolution dans la vue convolutive :
| Discrétisation | Bilinéaire | ZOH |
|---|---|---|
| Récurrence | \(\mathbf{\bar{A}} = (\mathbf {I} - \frac{\Delta}{2} \mathbf{A})^{-1}(\mathbf {I} + \frac{\Delta}{2} \mathbf{A})\) \(\mathbf {\bar{B}} = (\mathbf{I} - \frac{\Delta}{2} \mathbf{A})^{-1} \Delta \mathbf{B}\) \(\mathbf{\bar{C}} = \mathbf{C}\) |
\(\mathbf{\bar{A}} = e^{\mathbf{A}\Delta}\) \(\mathbf{\bar{B}} = (\mathbf{\bar{A}} - I)\mathbf{A}^{-1}\mathbf{B}\) \(\mathbf{\bar{C}} = \mathbf{C}\) |
| Convolution | \(\mathbf{\bar{K}}_k = (\mathbf{\bar{C}} \mathbf{\bar{B}}, \mathbf{\bar{C}} \mathbf{\bar{A}} \mathbf{\bar{B}}, …, \mathbf{\bar{C}} \mathbf{\bar{A}}^{k} \mathbf{\bar{B}})\) | \(\mathbf{\bar{K}} = (\ \mathbf{C} e^{\mathbf{A}\cdot k\Delta} (e^{\mathbf{A}\Delta} - I)\mathbf{A}^{-1}\mathbf{B}\ )_{0 \leq k < L}\) |
Pour la ZOH, après avoir déroulé les calculs, on obtient en fin de compte \(y_k = \sum_{j=0}^k \bar{C}\bar{A}^j\bar{B}\cdot u_{k-j} = \sum_{j=0}^k \bar{K}_j\cdot u_{k-j}\).
Calculer \(y\) à partir de \(u\) et \(\bar{K}\) s’effectue alors par Transformation de Fourier rapide (FFT) en \(O(L~log(L))\) avec \(L\) la longueur de la séquence en calculant simultanément la multiplication de deux polynômes de degrés \(L-1\).
2. DSSsoftmax et DSSexp
Version courte
GUPTA formule une proposition pour obtenir des DSS qui soient aussi expressifs que le S4, aboutissant à la formulation de deux DSS différents : le DSSexp et le DSSsoftmax. Les informations à retenir les concernant peuvent se résumer au tableau suivant :
| Approche | DSSexp | DSSsoftmax |
|---|---|---|
| Vue convolutive | \(K = \bar{K}_{\Delta, L}(\Lambda,\mathbb{I}_{1 \leq i \leq N},\ \widetilde{w})\\ = \widetilde{w} \cdot \Lambda^{-1} (e^{\Lambda\Delta} - I) \cdot \text{elementwise-exp}(P)\) | \(K = \bar{K}_{\Delta, L}(\Lambda,\ ((e^{L\lambda_i\Delta} - 1)^{-1})_{1\leq i \leq N},\ w)\\ = w \cdot \Lambda^{-1} \cdot \text{row-softmax}(P)\) |
| Vue récurrente | \(\bar{A} = \mathrm{diag}(e^{\lambda_1\Delta}, \ldots, e^{\lambda_N\Delta})\) \(\bar{B} = \left(\lambda_i^{-1} (e^{\lambda_i\Delta} - 1) \right)_{1\leq i \leq N}\) |
\(\bar{A} = \mathrm{diag}(e^{\lambda_1\Delta}, \ldots, e^{\lambda_N\Delta})\) \(\bar{B} = \left( {e^{\lambda_i\Delta} - 1 \over \lambda_i (e^{\lambda_i\Delta L} - 1)} \right)_{1\leq i \leq N}\) |
| Interprétation | Agit comme la porte d’oubli d’une LSTM | Si \(\Re(\lambda)<<0\) : conserve l’information locale, si \(\Re(\lambda)>>0\) : peut capturer des informations à très longues distances |
Nous travaillons donc ici sur \(ℂ\) et non pas \(ℝ\).
Version longue
GUPTA formule la proposition suivante pour obtenir des DSS qui sont aussi expressifs que le S4 :
Soit \(K \in \mathbb{R}^{1\times L}\) le noyau de longueur \(L\) d’un espace d’état donné \((A, B, C)\) et d’un temps d’échantillonnage \(\Delta > 0\), où \(A \in \mathbb{C}^{N \times N}\) est diagonalisable sur \(\mathbb{C}\) avec des valeurs propres \(\lambda_1,\ldots,\lambda_N\) et \(\forall i\), \(\lambda_i \neq 0\) et \(e^{L\lambda_i\Delta} \neq 1\). Soit \(P \in \mathbb{C}^{N \times L} P_{i,k} = \lambda_i k\Delta\) et \(\Lambda\) la matrice diagonale avec \(\lambda_1,\ldots,\lambda_N\). Alors il existe \(\widetilde{w}, w \in \mathbb{C}^{1\times N}\) tel que :
- (a) : \(K\ \ =\ \ \bar{K}_{\Delta, L}(\Lambda,\ (1)_{1 \leq i \leq N},\ \widetilde{w})\ \ =\ \ \widetilde{w} \cdot \Lambda^{-1} (e^{\Lambda\Delta} - I) \cdot \text{elementwise-exp}(P)\)
- (b) : \(K\ \ =\ \ \bar{K}_{\Delta, L}(\Lambda,\ ((e^{L\lambda_i\Delta} - 1)^{-1})_{1\leq i \leq N},\ w)\ \ =\ \ w \cdot \Lambda^{-1} \cdot \text{row-softmax}(P)\)
(a) suggère que nous pouvons paramétrer les espaces d’état via \(\Lambda, \widetilde{w} \in \mathbb{C}^N\) et calculer le noyau comme indiqué. Malheureusement, dans la pratique, la partie réelle des éléments de \(Λ\) peut devenir positive pendant l’apprentissage, le rendant instable pour les entrées longues. Pour résoudre ce problème, les auteurs proposent deux méthodes : DSSexp et DSSsoftmax.
2.1 Vue convolutive
Dans DSSexp, les parties réelles de \(Λ\) doivent être négatives. On a alors \(\Lambda = - \text{elementwise-exp}(\Lambda_\mathrm{re}) + i\cdot \Lambda_\mathrm{im}\) et \(\Delta = \mathrm{exp}(\Delta_{\log}) \in \mathbb{R}_{> 0}\). \(K\) se calcule alors comme dans la formule indiquée dans la partie (a) de la proposition.
Dans DSSsoftmax, chaque ligne de \(Λ\) est normalisée par la somme de ces éléments. On a \(\Lambda = \Lambda_\mathrm{re} + i\cdot \Lambda_\mathrm{im}\) et \(\Delta = \mathrm{exp}(\Delta_{\log}) \in \mathbb{R}_{> 0}\).
\(K\) se calcule alors comme dans la formule indiquée dans la partie (b) de la proposition.
A noter que softmax sur \(\mathbb{C}\) n’est pas forcément défini lors de sofmax \((0, i \pi)\), les auteurs utilisant une version corrigée du softmax pour prévenir ce problème (cf. annexe A.2. du papier).
2.2 Vue récurrente
Dans DSSexp, en utilisant la formule de la récurrence dans le tableau ci-dessus, on obtient \(\bar{A} = \mathrm{diag}(e^{\lambda_1\Delta}, \ldots, e^{\lambda_N\Delta})\) et \(\bar{B} = \left(\lambda_i^{-1} (e^{\lambda_i\Delta} - 1) \right)_{1\leq i \leq N}\), où dans les deux égalités, \(\lambda_i\) est la ième valeur propre de Lambda.
Etant donné que \(\bar{A}\) est diagonale, il est possible de calculer les \(x_k\) indépendamment de la manière suivante : \(x_{i,k} = e^{\lambda_i\Delta} x_{i,k-1} + \lambda_i^{-1} (e^{\lambda_i\Delta} - 1)u_k\).
Il est alors possible de déduire que, si \(|\lambda_i|\Delta \approx 0\), nous avons \(x_{i,k} \approx x_{i,k-1}\) permettant de copier l’histoire sur de nombreux pas de temps. En revanche, si \(\mathrm{Re}(\lambda_i)\Delta \ll 0\), alors \(_{i,k} \approx -\lambda_i^{-1}u_k\) et l’information des pas de temps précédents est oubliée, similaire à une porte « forget » dans les LSTMs.
Dans DSSsoftmax, en utilisant la formule de la récurrence du tableau ci-dessus, on obtient : \(\bar{A} = \mathrm{diag}(e^{\lambda_1\Delta}, \ldots, e^{\lambda_N\Delta})\) et \(\bar{B} = \left( {e^{\lambda_i\Delta} - 1 \over \lambda_i (e^{\lambda_i\Delta L} - 1)} \right)_{1\leq i \leq N}\).
D’où \(x_{i,k} = e^{\lambda_i\Delta} x_{i,k-1} + {u_k(e^{\lambda_i\Delta} - 1) \over \lambda_i (e^{\lambda_i\Delta L} - 1)}\).
A noter que \(e^{\lambda_i\Delta}\) peut être instable. Il faut alors calculer deux cas différents en fonction du signe de \(\mathrm{Re}(\lambda)\) en introduisant un état intermédiaire \(\widetilde{x}_{k}\).
• Si \(\mathrm{Re}(\lambda) \leq 0\) : \(\widetilde{x}_{k} = e^{\lambda\Delta}\cdot \widetilde{x}_{k-1} + u_k \ \ \ \ ,\ \ \ \ x_k = \widetilde{x}_k \cdot {(e^{\lambda\Delta} - 1) \over \lambda (e^{\lambda\Delta L} - 1) }\)
Et notamment si \(\mathrm{Re}(\lambda) \ll 0\) alors \(\widetilde{x}_k \approx u_k\) et \(x_k \approx u_k / \lambda\), entraînant une focalisation sur une information locale (les pas précédents sont ignorés).
• Si \(\mathrm{Re}(\lambda) > 0\) : \(\widetilde{x}_{k} = \widetilde{x}_{k-1} + e^{-k\lambda\Delta} \cdot u_k \ \ \ \ ,\ \ \ \ x_k = \widetilde{x}_k \cdot {e^{\lambda\Delta (k-(L-1))} \over \lambda}\cdot {e^{-\lambda\Delta}-1 \over e^{-\lambda\Delta L} - 1 }\)
De même si \(\mathrm{Re}(\lambda) \gg 0\) alors \(\widetilde{x}_0 \approx u_0\) et \(\widetilde{x}_k \approx \widetilde{x}_{k-1} \approx u_0\), \(x_{k < L-1} \approx 0\) et \(x_{L-1} \approx u_0 / \lambda\), le modèle peut ainsi capturer des informations à très longues distances. En pratique, les auteurs du S4D indiquant que \(\mathrm{Re}(\lambda) \gg 0\) ne fonctionne pas si \(L\) est très grande (explosion quand \(t \rightarrow \infty\) dans \(K(t) = C \exp(A^\intercal).B)\).
3. Initialisation
Les parties réelles et imaginaires de \(w\) sont initialisées à partir de \(\mathcal{N}(0,1)\), les éléments de \(\Delta_{\log}\) à partir de \(\exp(\mathcal{U}~(log(0.001), log(0.1)))\), et \(\Delta\) via les valeurs propres de la matrice HiPPO. Les auteurs se demandent s’il ne serait pas possible de trouver une initialisation plus simple pour \(\Delta\). Ils notent néanmoins qu’une aléatoire conduit à de moins bons résultats.
Concernant les résultats, DSS a été testé sur LRA et Speech Commands de WARDEN (2018) :
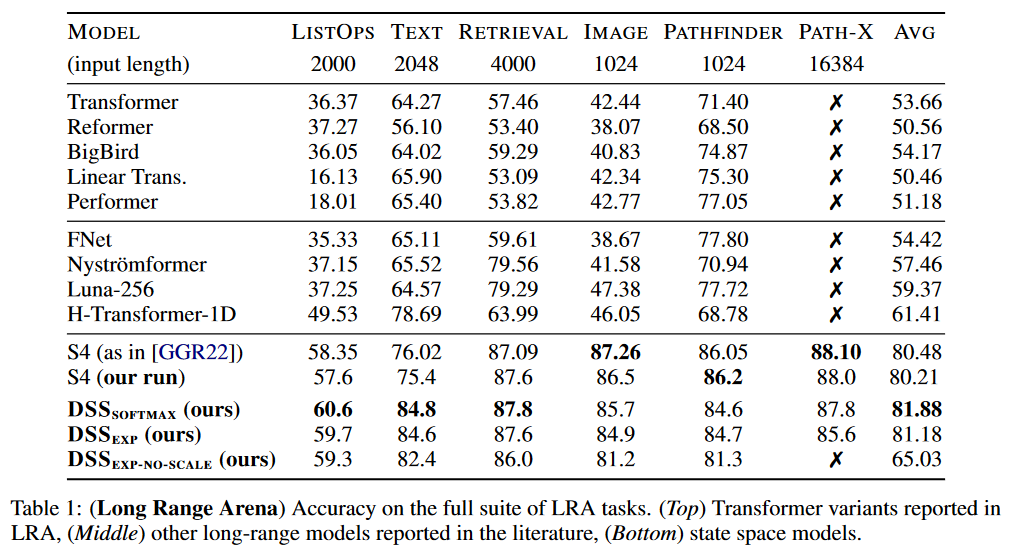 |
|---|
| Figure 6 : Résultats du DSS sur LRA |
Le DSS (en version softmax ou en version exp) obtient de meilleurs résultats moyens que ceux du S4 original pour ce benchmark. Le DSSsoftmax semble performer légèrement mieux que le DSSexp. Un intérêt également de ce papier est qu’il est le premier à reproduire les résultats du S4 et donc confirmer que les SSM passent ce benchmark.
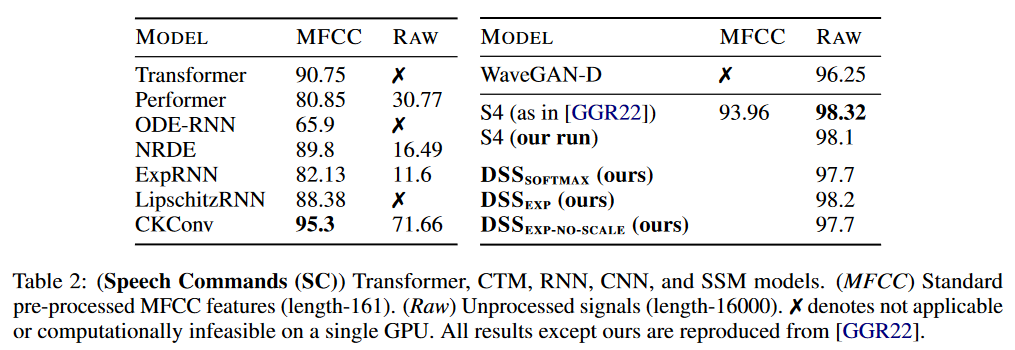 |
|---|
| Figure 7 : Résultats du DSS sur Speech Commands |
Sur Speech Commands, le S4 garde l’avantage sur les DSS.
Pour aller plus loin
L’implémentation officielle est disponible sur GitHub.
Ce papier a fait l’objet d’un spotlight talk à NeurIPS 2022.
Le S4D : le S4 diagonal
Le 23 juin 2022, GU, GUPTA et al. introduisent le S4D dans leur article On the Parameterization and Initialization of Diagonal State Space Models.
L’initialisation de la matrice d’état \(\mathbf{A}\) du DSS repose sur une approximation particulière de la matrice HiPPO du S4. Si la matrice du S4 possède une interprétation mathématique pour traiter les dépendances à longue portée, l’efficacité de l’approximation diagonale reste théoriquement inexpliquée.
Avec le S4D, les auteurs introduisent un SSM diagonal combinant le meilleur du calcul et de la paramétrisation de S4 et de l’initialisation de DSS. Au final, cela donne une méthode très simple, théoriquement fondée et empiriquement efficace.
Une comparaison des trois méthodes est donnée dans le tableau 1 du papier :
 |
|---|
| Figure 8 : Comparaison du S4, du DSS et du S4D |
Le S4D peut utiliser la discrétisation bilinéaire du S4 ou bien la discrétisation ZOH du DSS.
Dans le S4D, le noyau de convolution discrétisé de l’équation \(y = u \ast \mathbf{\overline{K}}\) se calcule de la façon suivante :
\(\mathbf{\overline{K}}_\ell = \sum_{n = 0}^{N-1} \mathbf{C}_n \mathbf{\overline{A}}_n^\ell \mathbf{\overline{B}}_n \implies \mathbf{\overline{K}} = (\mathbf{\overline{B}}^\top \circ \mathbf{C}) \cdot \mathcal{V}_L(\mathbf{\overline{A}})\)
où :
• \(\circ\) représente le produit matriciel d’Hadamard,
• \(\cdot\) un produit matriciel classique,
• \(\mathcal{V}_L\) est la matrice de Vandermonde c’est-à-dire : \(\mathcal{V} =
\begin{bmatrix}
1&\alpha _{1}&{\alpha _{1}}^{2}&\dots &{\alpha _{1}}^{n-1}\\
1&\alpha _{2}&{\alpha _{2}}^{2}&\dots &{\alpha _{2}}^{n-1}\\
1&\alpha _{3}&{\alpha _{3}}^{2}&\dots &{\alpha _{3}}^{n-1}\\
\vdots &\vdots &\vdots & \vdots \\
1&\alpha _{m}&{\alpha _{m}}^{2}&\dots &{\alpha _{m}}^{n-1}
\end{bmatrix}\).
Autrement dit, pour tout \(i\) et \(j\), le coefficient en ligne \(i\) et colonne \(j\) est \(\displaystyle V_{i,j}={\alpha _{i}}^{j-1}\).
Au final, dans le S4D,
\(\mathbf{\overline{K}} =
\begin{bmatrix}
\mathbf{\overline{B}}_0 \mathbf{C}_0 & \dots & \mathbf{\overline{B}}_{N-1} \mathbf{C}_{N-1}
\end{bmatrix}
\begin{bmatrix}
1 & \mathbf{\overline{A}}_0 & \mathbf{\overline{A}}_0^2 & \dots & \mathbf{\overline{A}}_0^{L-1} \\
1 & \mathbf{\overline{A}}_1 & \mathbf{\overline{A}}_1^2 & \dots & \mathbf{\overline{A}}_1^{L-1} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & \mathbf{\overline{A}}_{N-1} & \mathbf{\overline{A}}_{N-1}^2 & \dots & \mathbf{\overline{A}}_{N-1}^{L-1} \\
\end{bmatrix}
\qquad \text{où } \mathcal{V}_L(\mathbf{\overline{A}})_{n, \ell} = \mathbf{\overline{A}}_n^\ell\).
Le tout est calculable en \(O(N+L)\) opérations et espace.
La paramétrisation des différentes matrices est la suivante :
- \(\mathbf{A} = -\exp(\Re(\mathbf{A})) + i \cdot \Im(\mathbf{A})\).
Les auteurs indiquent qu’il est possible de remplacer l’exponentielle par n’importe quelle fonction positive. - \(\mathbf{B} = 1\) puis est entraîné
- \(\mathbf{C}\) aléatoire avec un écart-type de 1 puis entraîné.
Notons que le S4 prend en compte des réels alors que S4D des complexes en paramétrant avec une taille d’état de \(N/2\) et en ajoutant implicitement les paires conjuguées aux paramètres. On a alors l’équivalent de \(N\) paramètres réels assurant que la sortie est réelle.
Concernant l’initialisation, les auteurs en introduisent deux :
• S4D-Inv qui est une approximation de S4-LegS : \(\quad \mathbf{A}_n = -\frac{1}{2} + i \frac{N}{\pi} \left( \frac{N}{2n+1}-1 \right)\)
• S4D-Lin qui est une approximation de S4-FouT : \(\quad \mathbf{A}_n = -\frac{1}{2}\mathbf{1} + i \pi n\)
Nous invitons le lecteur à consulter la partie 4 du papier pour plus de détails concernant ces équations.
D’un point de vue interprétabilité, la partie réelle de \(\mathbf{A}_n\) contrôle le taux de décroissance des poids. La partie imaginaire de \(\mathbf{A}_n\) contrôle quant à elle les fréquences d’oscillations de la fonction de base \(K_n(t) = e^{t\mathbf{A}}\mathbf{B}\).
Enfin les auteurs avancent quelques résultats :
1) Calculer le modèle avec une softmax au lieu de Vandermonde ne fait pas de grande différence
2) Entraîner B donne toujours de meilleurs résultats.
3) Il n’existe pas de différences notables entres les deux discrétisations possibles.
4) Restreindre la partie réelle de A conduit à de meilleurs résultats (pas de façon significative néanmoins)
5) Toutes les modifications testées pour l’initialisation ont dégradé les résultats. A savoir appliquer un coefficient sur la partie imaginaire ou utiliser une partie imaginaire aléatoire / utiliser une partie réelle aléatoire / utiliser une partie imaginaire et une partie réelle aléatoire.
Cette méthode étant très facile à implémenter par rapport aux autres (Vandermade se limitant à deux lignes de code), le S4D a remplacé le S4 dans les usages (on peut d’ailleurs observer des abus de langage où dans la table 6 du papier du Mamba par exemple, les auteurs utilisent le terme S4 pour désigner le S4D).
Pour aller plus loin
L’implémentation officielle est disponible sur GitHub.
Le 1er décembre 2022, GUPTA et al. présentent une suite au DSS avec Simplifying and Understanding State Space Models with Diagonal Linear RNNs qui introduit le DLR. Ils se débarrassent de l’étape de discrétisation et proposent un modèle basé sur des RNN linéaires diagonaux (DLR) pouvant opérer sur environ 1 million de positions (contrairement aux RNN classiques). Le code de ce modèle est disponible sur GitHub.
Le GSS : Gated State Space
Cinq jours après le S4D, le 27 juin 2022, MEHTA, GUPTA et al. introduisent le GSS dans leur papier Long Range Language Modeling via Gated State Spaces.
Dans ce travail, ils se concentrent sur la modélisation de séquences autorégressives (là où les travaux précédents sur les SSM se concentraient particulièrement sur les tâches de classification de séquences) à partir de livres en anglais, de code source Github et d’articles de mathématiques ArXiv. Ils montrent que leur couche appelée Gated State Space (GSS) s’entraîne significativement plus vite que le DSS (2 à 3 fois plus vite). Ils attestent également que l’exploitation de l’auto-attention pour modéliser les dépendances locales améliore encore les performances du GSS.
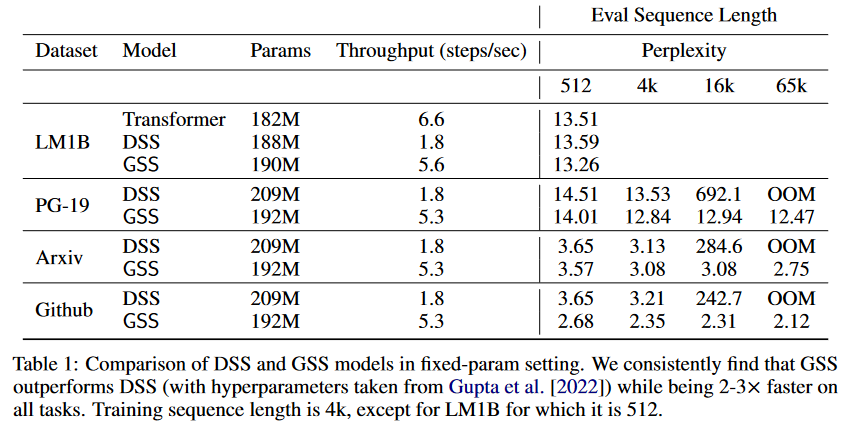 |
|---|
| Figure 9 : Comparaison du DSS vs GSS. Les modèles sont entraînés sur des séquences de longueurs 4K puis évalués sur des séquences pouvant aller jusqu’à 65K tokens. |
Partant du constat que les SSM (S4/DSS) s’entraînent plus lentement que prévu sur TPU, les auteurs ont modifié l’architecture afin de réduire la dimensionnalité d’opérations spécifiques qui se sont révélées être des goulots d’étranglement. Ces modifications s’inspirent d’une observation empirique bien étayée concernant l’efficacité des unités de gating (Language Modeling with Gated Convolutional Networks de DAUPHIN et al. (2016), GLU Variants Improve Transformer de SHAZEER (2020), etc.). Plus précisément, les auteurs s’inspirent du papier Transformer Quality in Linear Time de HUA et al. (2022). Ces derniers ont montré qu’avec leur modèle FLASH, le remplacement de la couche feed-forward dans le Transformer par des unités de gating permet d’utiliser une attention unitête plus faible avec une perte de qualité minimale. Ils ont appelé cette composante la Gated Attention Unit (GAU).
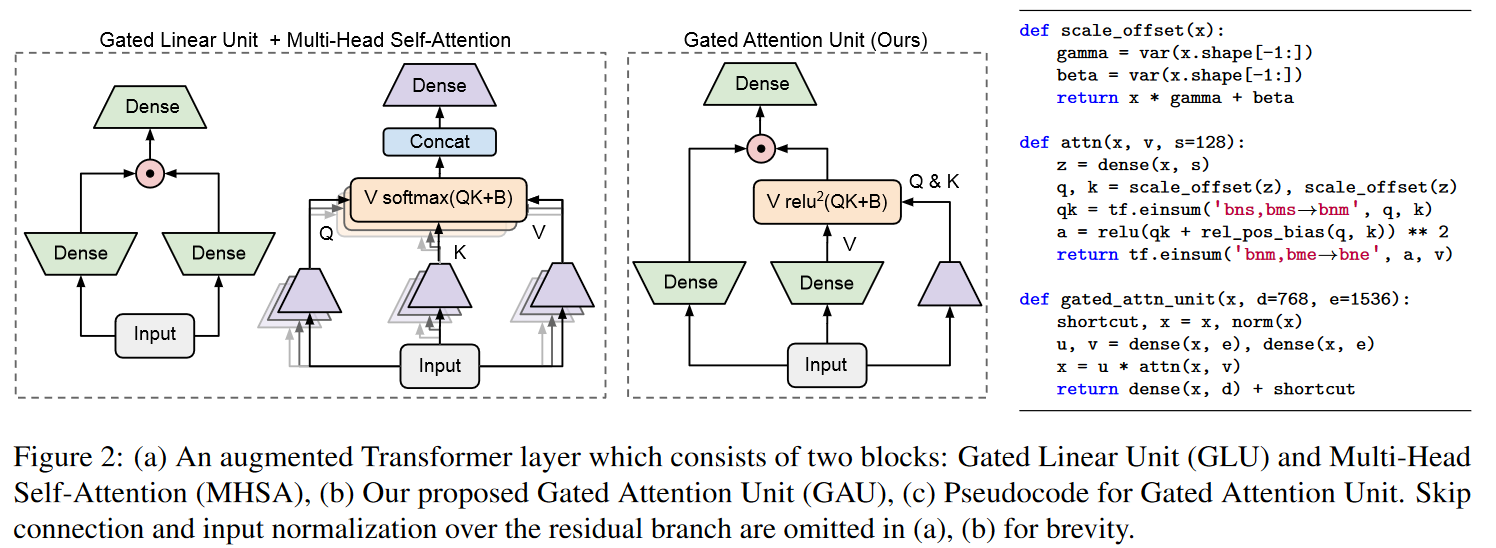 |
|---|
| Figure 10 : La Gated Attention Unit. Ce n’est pas exactement la même figure que celle du papier : j’ai effectué une translation horizontale afin d’avoir l’entrée en bas et non en haut pour faciliter le parallèle avec la figure du Mega visible plus bas. |
Les auteurs du GSS ont donc étendu l’utilisation des gating units aux SSM et observent alors une réduction de la dimensionnalité lors de l’exécution d’opérations FFT.
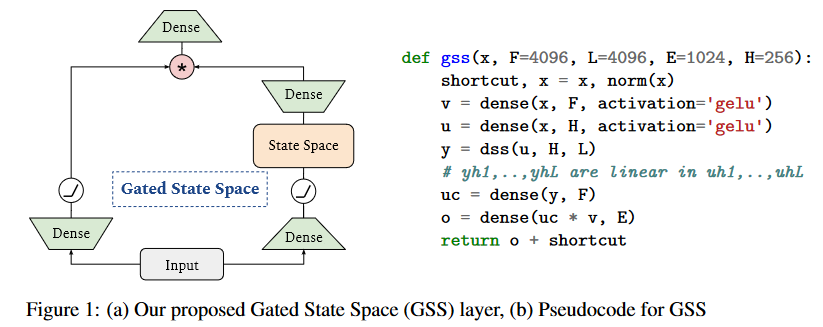 |
|---|
| Figure 11 : Adaptation de la GAU aux SSM. |
A noter que contrairement à HUA et al., les auteurs n’observent pas beaucoup d’avantages à utiliser les activations RELU² ou Swish au lieu de la GELU d’où sa conservation.
De plus, le DSS utilise un pas de temps \(∆\) fixé à 1 (les auteurs observant que cela permet de réduire le temps de calcul nécessaire à la création des noyaux et de simplifier leur calcul).
Un point particulièrement intéressant est que contrairement aux observations réalisées dans le S4 et le DSS, la performance du modèle sur les tâches de modélisation du langage s’est retrouvée beaucoup moins sensible à l’initialisation permettant alors d’entraîner le modèle avec succès en initialisant les variables de l’espace d’état de manière aléatoire. Cela constitue un résultat très important puisqu’il montre que ni la matrice HiPPO (S4), ni l’initialisation HiPPO (DSS) ne sont nécessaires.
Concernant l’hybride GSS-Transformer, il consiste simplement à intercaler avec parcimonie des blocs Transformer traditionnels avec des couches GSS. Le modèle hybride obtient une perplexité plus faible que le modèle purement SSM :
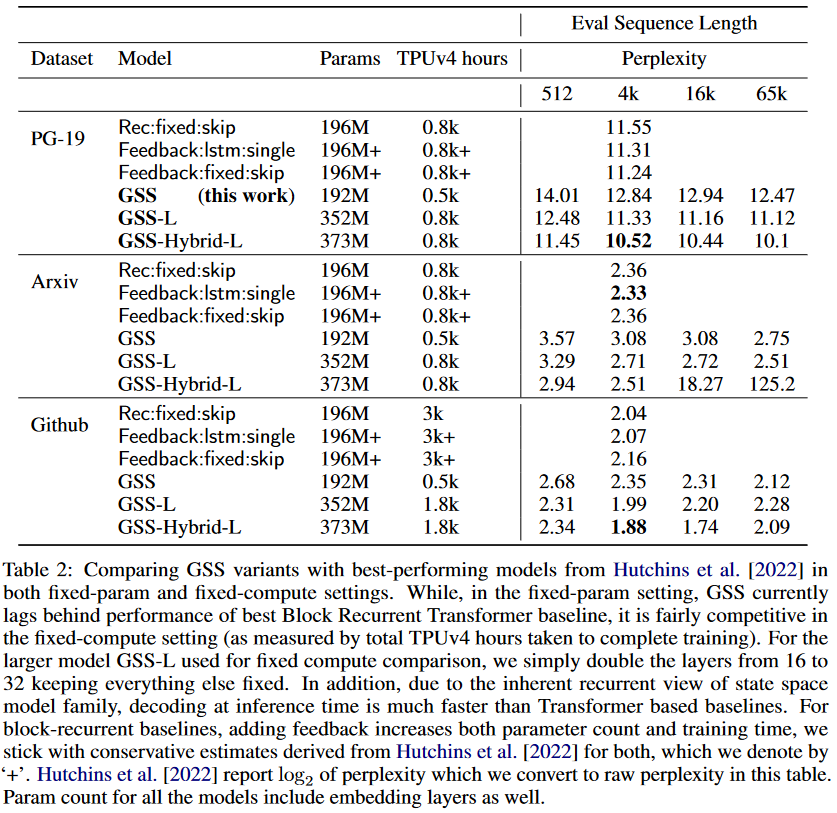 |
|---|
| Figure 12 : Performances du modèle hybride GSS-Transformer. |
Pour aller plus loin
L’implémentation officielle est disponible sur GitHub.
Mega
Le 21 septembre 2022, MA, ZHOU et al., ont publié le Mega: Moving Average Equipped Gated Attention.
Le Mega est un transformer avec un mécanisme d’attention à une seule tête, utilisant le système de portes du GAU, et est équipé d’une moyenne mobile exponentielle (EMA) amortie pour incorporer le biais inductif positionnel.
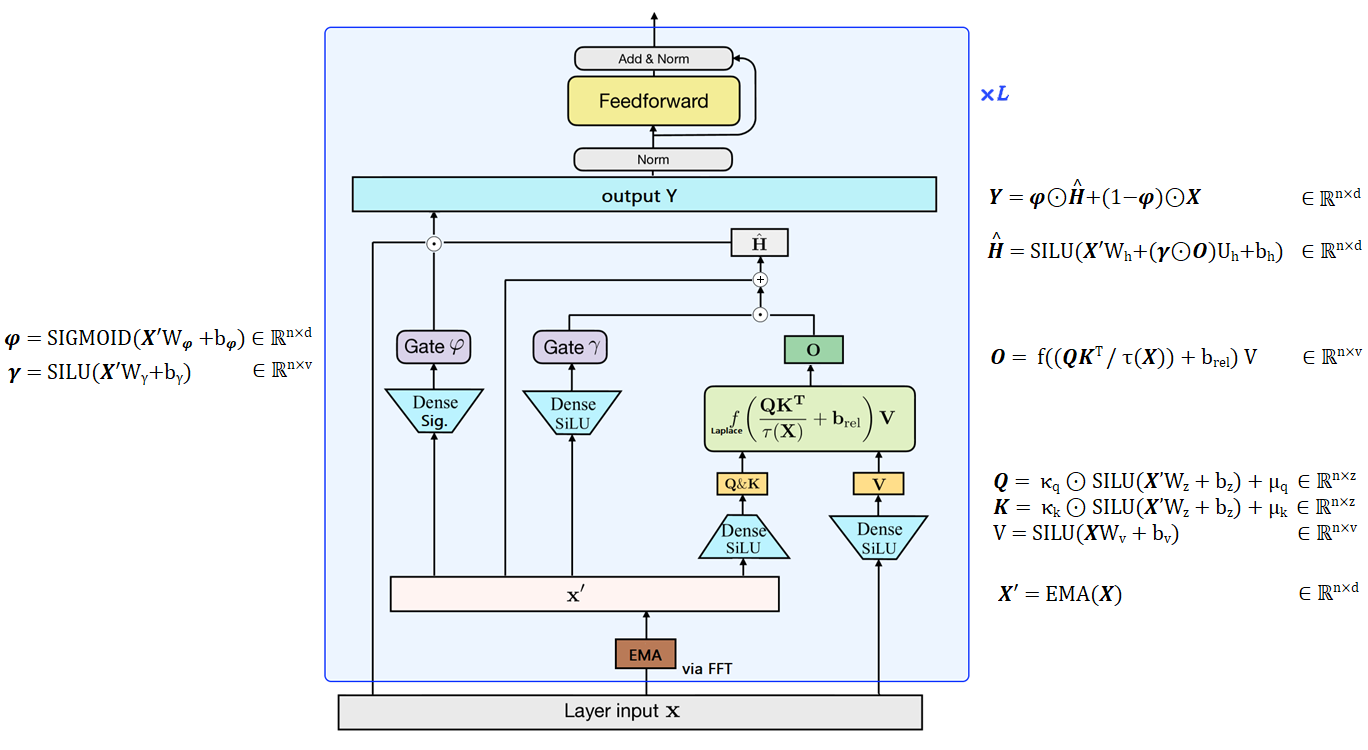 |
|---|
| Figure 13 : Vue d’ensemble du Mega, figure conçue à partir de ma compréhension du papier. Les auteurs remplacent la RELU² du GAU par une fonction de Laplace qui est plus stable (cf. la figure 4 dans le papier). |
Les auteurs proposent aussi une variante, Mega-chunk, qui divise efficacement l’ensemble de la séquence en plusieurs morceaux de longueur fixe. Ils reprennent ici le principe déjà présent et expliqué dans le modèle FLASH (cf. la figure 4 du papier de ce modèle). Cela offre une complexité linéaire en termes de temps et d’espace avec une perte de qualité minimale.
 |
|---|
| Figure 14 : Le Mega chunk |
Cela offre une complexité linéaire appliquant simplement l’attention localement à chaque morceau de longueur fixe.
Plus précisément, on divise les séquences de requêtes, de clés et de valeurs en morceaux de longueur \(c\). Par exemple, \(\mathbf{Q} = {\mathbf{Q}_1, ... , \mathbf{Q}_k}\), où \(k = -\frac{n}{c}\) est le nombre de morceaux. L’opération d’attention est appliquée individuellement à chaque bloc, ce qui donne une complexité linéaire \(\mathcal{O}(kc^2) = \mathcal{O}(nc)\) par rapport à \(n\).
Cette méthode souffre néanmoins d’une limitation critique, à savoir la perte d’informations contextuelles provenant d’autres blocs. Mais la sous-couche EMA atténue ce problème en capturant les informations contextuelles locales à proximité de chaque token dont les résultats sont utilisés comme entrées dans la sous-couche d’attention. Ainsi, le contexte effectif exploité par l’attention au niveau du bloc peut aller au-delà de la limite du bloc.
Le Mega est extrêmement compétitif puisqu’il devient alors le meilleur modèle sur le LRA :
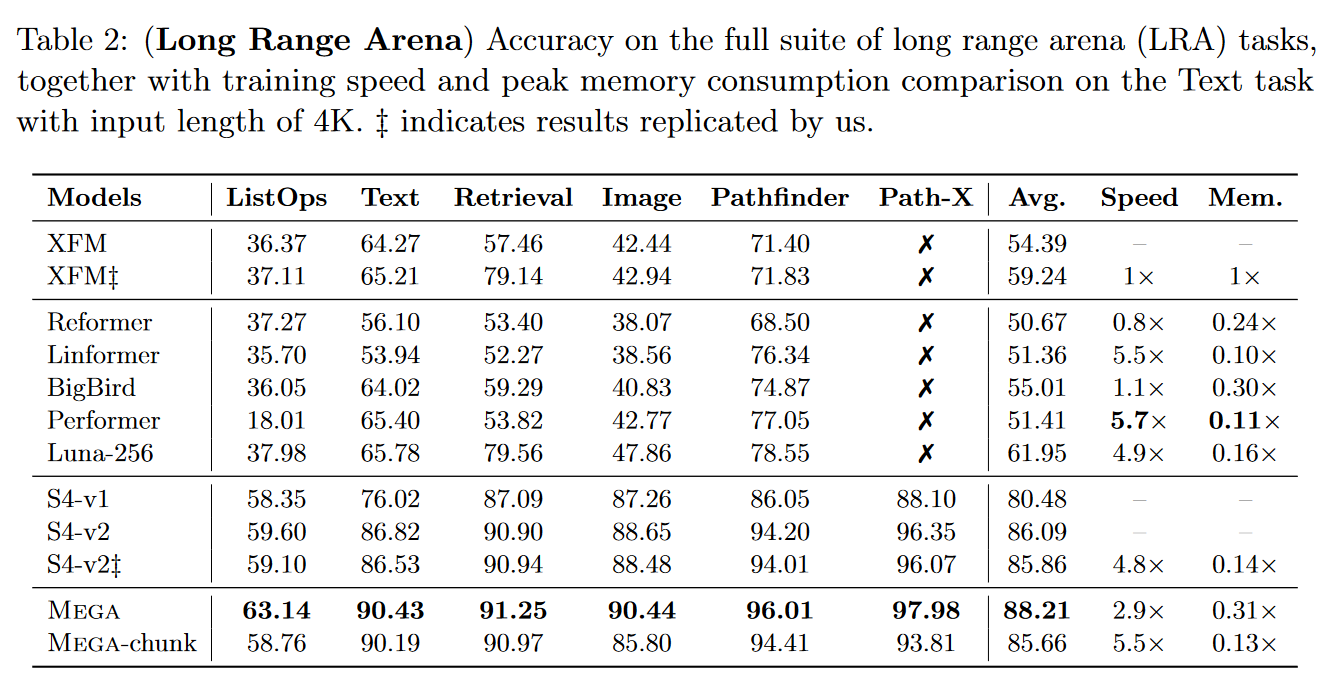 |
|---|
| Figure 15 : Les résultats du Mega sur le benchmark LRA |
Que fait donc un transformer dans un article de blog sur les SSM ? Intéressons-nous à l’EMA amortie pour comprendre le lien entre le Mega et le S4D.
• Rappel sur l’EMA « classique » :
L’équation d’une EMA « classique » est \(𝐲_t = 𝜶 ⊙ 𝐱_t + (1−𝜶) ⊙ 𝐲_{t−1}\) avec \(𝜶\) in \([0,1]^d\) le coefficient de l’EMA représentant le degré de diminution de la pondération et ⊙ le produit matriciel de Hadamard.
Un 𝜶 plus élevé décote plus rapidement les observations les plus anciennes.
On impose donc ici un biais inductif : le poids de la dépendance entre deux tokens diminue de manière exponentielle au fil du temps avec un facteur 𝜶 agnostique à l’entrée. Cette propriété favorise les dépendances locales et limite les dépendances à long terme.
Le calcul de l’EMA peut être représenté comme n convolutions individuelles pouvant être calculées efficacement par FFT.
• EMA utilisée dans le Mega :
Le Mega utilise une EMA « amortie » multidimensionnelle. C’est-à-dire que dans l’équation de l’EMA « amortie », \(𝐲_t = 𝜶 ⊙ 𝐱_t + (1−𝜶 ⊙ 𝜹) ⊙ 𝐲_{t−1}\) où un paramètre \(𝜹\) in \([0,1]^d\) est introduit qui représente le facteur d’amortissement, \(x\) est étendue à \(h\) dimensions via une matrice d’expansion \(𝜷\) in \(R^{d \times h}\).
L’équation devient alors \(𝐲_{t,j} = 𝜼_j^{\intercal} 𝐡_t^{(j)}\) avec \(𝐡_t^{(j)} = 𝜶_j ⊙ 𝐮_t^{(j)}+ (1−𝜶_j ⊙ 𝜹_j) ⊙ 𝐡_{t−1}^{(j)}\) et \(𝜼 \in R^{d \times h}\) est la matrice de projection qui renvoie l’état caché en \(h\) dimension à la sortie unidimensionnelle \(𝐲_{t,j} \in \mathbb{R}\).
Preuve que l’ EMA « amortie » multidimensionnelle peut être calculée comme une convolution et donc par FTT (en fixant \(d = 1\) pour \(𝜶\) et \(𝜹\)) :
On a \(𝐲_t = 𝜼^{\intercal} 𝐡_t\) avec \(𝐡_t = 𝜶_j ⊙ 𝐮_t + (1−𝜶 ⊙ 𝜹) ⊙ 𝐡_{t−1}\). Notons \(ϕ = 1−𝜶 ⊙ 𝜹\).
Alors : \(𝐡_t = 𝜶 ⊙ 𝐮_t + (1−𝜶 ⊙ 𝜹) ⊙ 𝐡_{t−1} = 𝜶 ⊙ 𝜷 𝐱_t + ϕ ⊙ 𝐡_{t−1}\)
et \(𝐲_t = 𝜼^{\intercal} 𝐡_t = 𝜼^{\intercal} (𝜶 ⊙ 𝜷 𝐱_t + ϕ ⊙ 𝐡_{t−1})\)
Ensuite, en déroulant les deux équations ci-dessus, on obtient explicitement :
Etape 0 : \(𝐡_1 = 𝜶 ⊙ 𝜷𝐱_1 + ϕ ⊙ 𝐡_0\)
Etape 1 : \(𝐡_2 = 𝜶 ⊙ 𝜷𝐱_2 + ϕ ⊙ 𝐡_1\)
\(= 𝜶 ⊙ 𝜷 𝐱_2 + ϕ ⊙ (ϕ ⊙ 𝐡_0 + 𝜶 ⊙ 𝜷 𝐱_1) = 𝜶 ⊙ 𝜷 𝐱_2 + ϕ^2 ⊙ 𝐡_0 + ϕ ⊙ 𝜶 ⊙ 𝜷 𝐱_1\)
…
Et de même :
Etape 0 : \(𝐲_1 = 𝜼^{\intercal} 𝜶 ⊙ 𝜷 𝐱_1 + ϕ ⊙𝐡0) = 𝜼^{\intercal} 𝜶 ⊙ 𝜷 𝐱_1 + 𝜼^{\intercal} ϕ ⊙ 𝐡_0\)
Etape 1 : \(𝐲_2 = 𝜼^{\intercal} 𝜶 ⊙ 𝜷 𝐱_2 + 𝜼^{\intercal} ϕ ⊙ 𝐡_1\)
\(= 𝜼^{\intercal} 𝜶 ⊙ 𝜷 𝐱_2 + 𝜼^{\intercal} ϕ ⊙ (𝜶 ⊙ 𝜷 𝐱_1 + ϕ ⊙ 𝐡_0) = 𝜼^{\intercal} 𝜶 ⊙ 𝜷 𝐱_2 + 𝜼^{\intercal} ϕ ⊙ 𝜶 ⊙ 𝜷 𝐱_1 + 𝜼^{\intercal} ϕ^2 ⊙ 𝐡_0\)
…
Etape \(t\) : \(𝐲_t = 𝜼^{\intercal} 𝜶 ⊙ 𝜷 𝐱_t + … + 𝜼^{\intercal} ϕ_{t−1} ⊙ 𝜶 ⊙ 𝜷 𝐱_{t−1} + 𝜼^{\intercal} ϕ^t ⊙ 𝐡_0\).
Et donc \(𝐲 = \mathbf{K} * 𝐱 + 𝜼^{\intercal} ϕ^t ⊙ 𝐡_0\) avec \(𝒦 = (𝜼^{\intercal} (𝜶 ⊙ 𝜷), 𝜼^{\intercal} (ϕ ⊙ 𝜶 ⊙ 𝜷), …, 𝜼^{\intercal}(ϕ^t ⊙ 𝜶 ⊙ 𝜷) \in \mathbb{R}^n\).
\(\mathbf{K}\) est calculé dans le Mega via le produit de Vandermonde, ce qui nous rappelle la méthode utilisée dans le S4D.
Pour aller plus loin
L’implémentation officielle est disponible sur GitHub.
Le modèle est également disponible sur Transformers.
Pour plus de détails sur les liens entre le Mega et le S4, le lecteur est invité à consulter les messages échangés entre Albert GU et les auteurs du Mega trouvables en commentaires de la soumission du Mega sur Open Review. En résumé, en établissant un lien entre l’étape de discrétisation des SSM et l’EMA amortie, il est possible de voir le Mega vue comme un hybride SSM/Attention simplifiant le S4 pour qu’il soit à valeur réelle plutôt que complexe.
Liquid-S4 : Liquid Structural State-Space Models
Le 26 septembre 2022, HASANI, LECHNER et al. mettent en ligne Liquid Structural State-Space Models introduisant le Liquid-S4.
Dans ce papier, les auteurs utilisent la formulation des SSM structurels (S4) pour obtenir des instances de réseaux liquides linéaires possédant les capacités d’approximation du S4 et des LTC (liquid time-constant).
Les réseaux neuronaux LTC sont des réseaux neuronaux causaux à temps continu dotés d’un module de transition d’état dépendant des entrées, leur permettant d’apprendre à s’adapter aux entrées lors de l’inférence. Il est possible de voir cela comme une sorte de mécanisme de sélection.
Pour en savoir plus sur les réseaux liquides, vous pouvez consulter un papier précédent par les mêmes auteurs : Liquid Time-constant Networks (2021).
Dans le cadre du Liquid-S4, il faut simplement savoir que l’état d’un LTC à chaque pas de temps est donné par :
\begin{equation}
\frac{d\textbf{x}(t)}{dt} = - \underbrace{\Big[\mathbf{A} + \mathbf{B} \odot f(\textbf{x}(t),\textbf{u}(t), t, \theta)\Big]}_\text{Liquid time-constant} \odot \textbf{x}(t) + \mathbf{B} \odot f(\textbf{x}(t), \textbf{u}(t), t, \theta).
\end{equation}
Avec :
- \(\textbf{x}^{(N \times 1)}(t)\) est le vecteur de l’état caché de taille $N$,
- \(\textbf{u}^{(m \times 1)}(t)\) est un signal d’entrée avec $m$ caractéristiques,
- \(\mathbf{A}^{(N \times 1)}\) est un mécanisme de transition d’état constant dans le temps,
- \(\mathbf{B}^{(N \times 1)}\) est un vecteur de biais
- \(\odot\) représente le produit d’Hadamard
- \(f(.)\) est une non-linéarité bornée paramétrée par $\theta$.
En pratique, un SSM utilisant un réseau liquide se formule via le système d’équations différentielles suivant :
\[\begin{aligned} x' &= (\mathbf{A} + \mathbf{B} u) x + \mathbf{B}u\\ y &= \mathbf{C}x \end{aligned}\]Ce système dynamique peut être résolu efficacement via la même paramétrisation que le S4, en donnant lieu à un noyau convolutif supplémentaire qui prend en compte les similitudes des signaux décalés. Le modèle obtenu est le Liquid-S4. Explicitons ceci avec un peu de maths.
La vue récurrente du Liquid-S4 est obtenue en discrétisant le système avec la règle des trapèzes (forme bilinéaire). On obtient alors : \begin{align} x_k = \big( \overline{\textbf{A}} + \overline{\textbf{B}}~u_k\big)~x_{k-1} + \overline{\textbf{B}}~u_k,~~~~~~y_k = \overline{\textbf{C}}~x_k \end{align}
Comme pour le S4, la vue convolutive est obtenue en déroulant la vue récurrente dans le temps (en supposant \(x_{-1} = 0\)) :
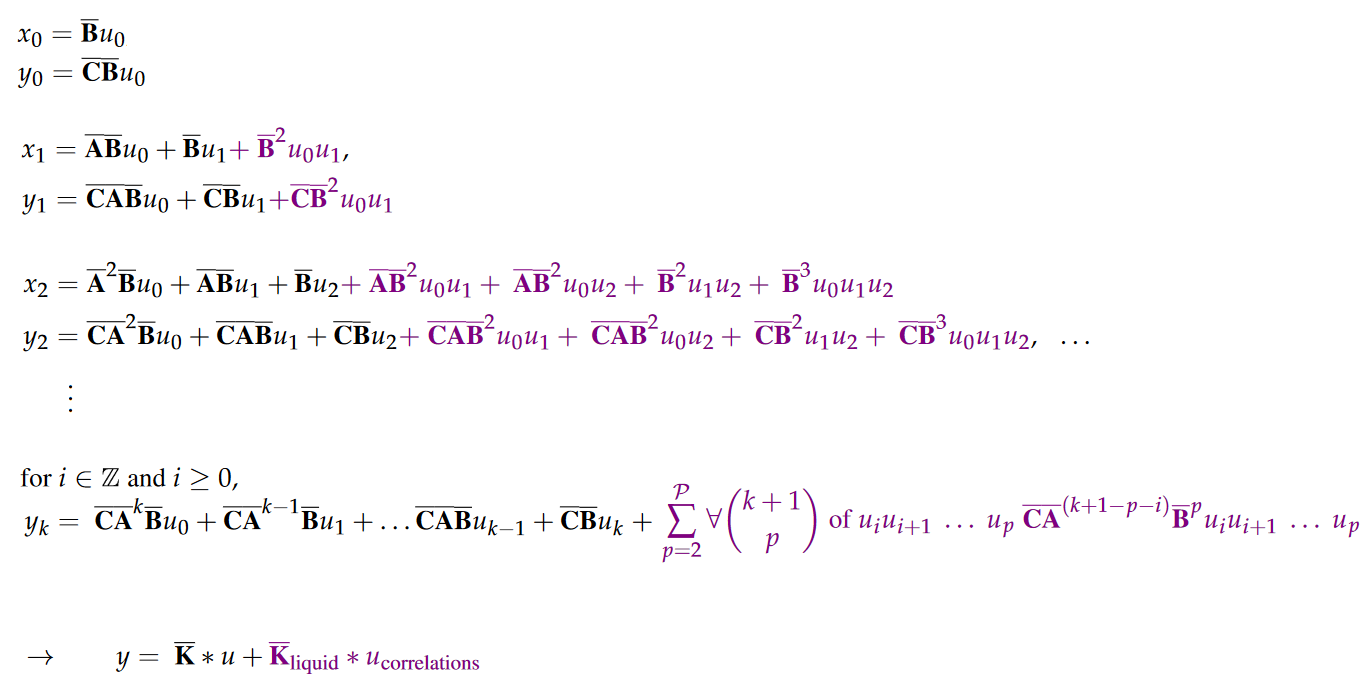 |
|---|
| Figure 16 : La partie en violet ne s’affichant pas sur mon blog, je dois passer par une image :/ |
Vous pouvez voir deux couleurs dans les formules. Elles correspondent à deux types de configurations de poids :
- En noir, les poids des entrées temporelles individuelles indépendantes, i.e le noyau convolutif du S4.
- En violet, les poids associés à tous les ordres d’auto-corrélation du signal d’entrée. Il s’agit d’un noyau de corrélation d’entrée supplémentaire, appelé noyau liquide par les auteurs.
Finalement le noyau de convolution s’exprime de la façon suivante : \(\overline{\textbf{K}}_{\text{liquid}} \in \mathbb{R}^{\tilde{L}} := \mathcal{K}_L(\overline{\textbf{C}},\overline{\textbf{A}},\overline{\textbf{B}}) := \big(\overline{\textbf{C}}\overline{\textbf{A}}^{(\tilde{L}-i-p)}\overline{\textbf{B}}^p\big)_{i \in [\tilde{L}],~ p \in [\mathcal{P}]} = \big( \overline{\textbf{C}}\overline{\textbf{A}}^{\tilde{L}-2}\overline{\textbf{B}}^2, \dots, \overline{\textbf{C}}\overline{\textbf{B}}^p \big)\)
Les auteurs montrent ensuite que ceci est calculable efficacement via un processus semblable à ce qui a été appliqué dans le S4 (HiPPO, Woodbury, Transformée de Fourier inverse, etc.). Nous invitons le lecteur à consulter l’algorithme 1 dans le papier pour plus de détails.
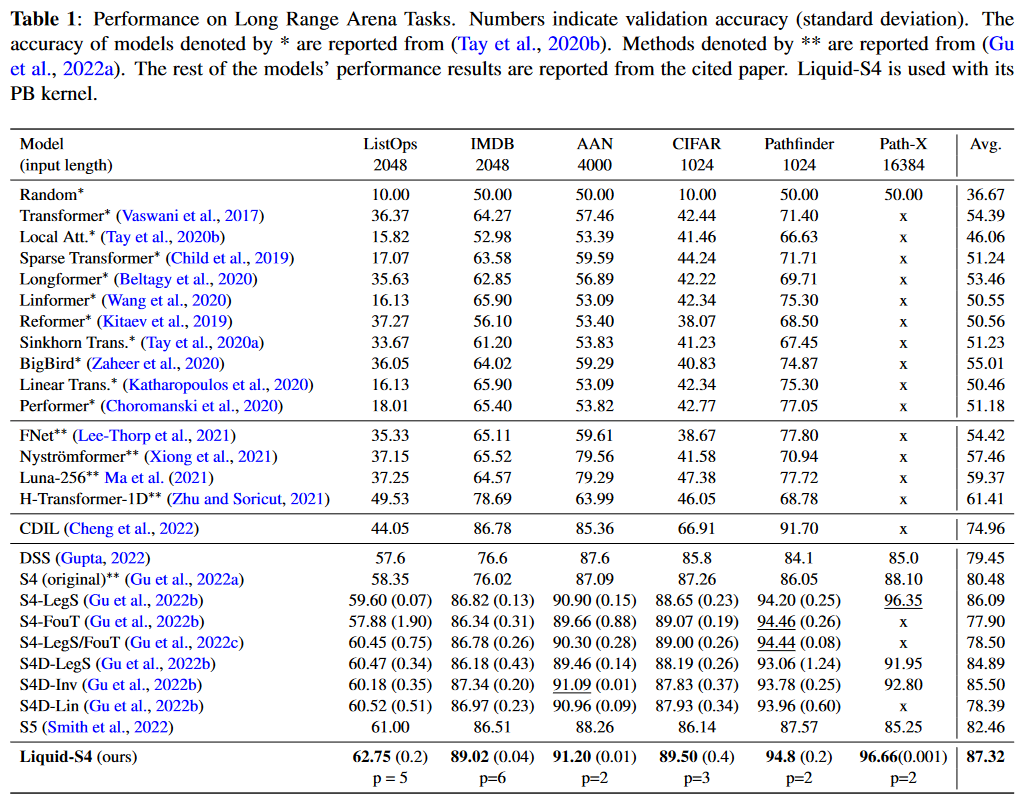
Testée sur le LRA, cette approche apparaît comme la meilleure. Seul Mega, publié sept jours plus tôt et donc non présent dans le papier, fait mieux :
 |
|---|
| Figure 17 : Les résultats du Liquid-S4 sur le benchmark LRA |
HASANI, LECHNER et al. appliquent leur modèle également sur les jeux de données Speech Commands, sCIFAR et BIDMC Vital Signs de PIMENTEL et al., et y établissent le nouvel état de l’art.
Pour aller plus loin
L’implémentation officielle est disponible sur GitHub.
Les échanges sur Open Review.
L’implémentation officielle des LTC sur GitHub.
Le S5 : Simplified State Space Layers for Sequence Modeling
Chronologiquement, le Simplified State Space Layers for Sequence Modeling de SMITH, WARRINGTON et LINDERMAN introduisant le modèle S5 a été dévoilé le 9 août 2022, donc avant le Mega et le Liquid-S5. Cependant j’aborde ce papier après ces derniers car le 6 octobre 2022, les auteurs du S5 ont procédé à une actualisation de leur publication améliorant leur modèle de plus de 5 points sur le LRA par rapport à la V1. De plus, ils proposent une comparaison portant sur l’ensemble des SSM sortis en 2022. Cela me paraissait plus pertinent d’aborder le S5 à partir de sa V2.
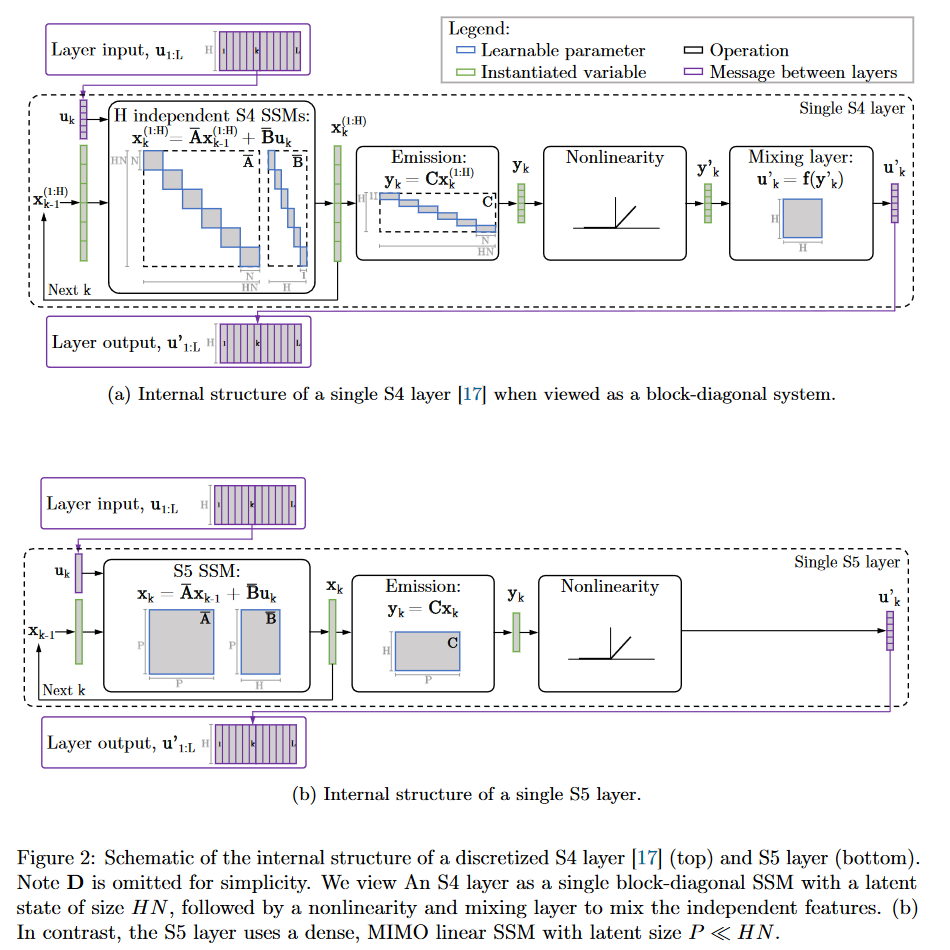
Dans le S5, les auteurs proposent de remplacer la formulation du S4 utilisant une banque de SSM indépendants entrée unique/sortie unique (SISO pour single-input, single-output) par un SSM à entrée multiple/sortie multiple (MIMO pour multi-input, multi-output) qui a une dimension latente réduite.
 |
|---|
| Figure 18 : Le comportement interne du S4 vs celui du S5 |
La dimension latente réduite du système MIMO permet l’utilisation de l’algorithme parallel scan qui simplifie les calculs nécessaires pour appliquer la couche S5 en tant que transformation séquence à séquence. Le modèle résultant perd ainsi la vue convolutive du SSM pour se focaliser uniquement sur la vue récurrente (obtenue par discrétisation ZOH). Le parti pris des auteurs est donc d’opérer sur le domaine temporel plutôt que celui fréquentiel. Ils utilisent une approximation diagonale de la matrice HiPPO leur permettant d’avoir une initialisation et une paramétrisation efficaces adaptées à leur système MIMO.
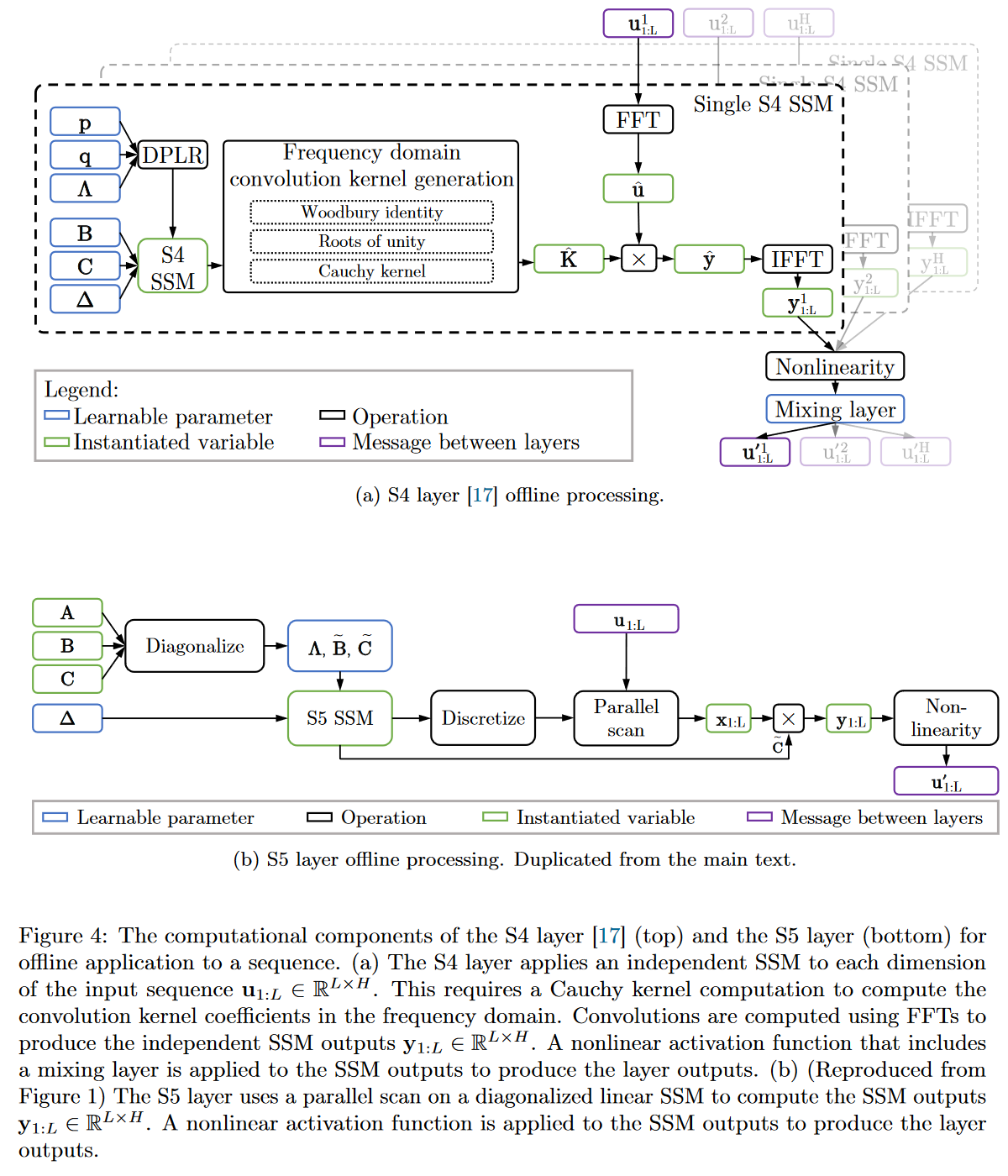 |
|---|
| Figure 19 : Comparaison complète du fonctionnement du S4 vs celui du S5 |
L’utilisation du parallel scan étant un composant repris dans d’autres SSM par la suite (le Mamba notamment), détaillons un peu son fonctionnent dans le cadre du S5 afin de se familiariser avec cet algorithme dès cet article. Pour cela le plus simple est de reprendre l’exemple donné dans l’appendix H du papier où les auteurs l’appliquent sur une séquence de longeur \(L = 4\).
Pour calculer un parallel scan deux choses sont nécessaires :
- Les éléments initiaux sur lesquels l’analyse va opérer.
Nous définissons les éléments initiaux d’une séquence de longueur \(L\) comme, \(c_{1:L}\), de sorte que chaque élément \(c_k\) soit le tuple \(c_k = (c_{k,a}, c_{k,b}) := (\overline{\mathbf{A}},\enspace \overline{\mathbf{B}}u_k)\). Dans le cas de \(L = 4\), nous avons donc \((\overline{\mathbf{A}},\enspace \overline{\mathbf{B}}u_1), (\overline{\mathbf{A}},\enspace \overline{\mathbf{B}}u_2),(\overline{\mathbf{A}},\enspace \overline{\mathbf{B}}u_3)\) et \((\overline{\mathbf{A}},\enspace \overline{\mathbf{B}}u_4)\). - Un opérateur associatif binaire \(\bullet\) utilisé pour combiner les éléments. Mathématiquement, un opérateur associatif binaire étant \(I \bullet J \bullet K = (I \bullet J)\bullet K = I \bullet (J \bullet J)\).
Si nous devions procéder de manière séquentielle avec le scan, en posant \(s_0:=(\mathbf{I},0)\), nous devrions effectuer 4 calculs pour obtenir les 4 sorties \(s_i\) :
\(s_1 = s_0 \bullet c_1 = (\mathbf{I},\enspace 0) \bullet (\overline{\mathbf{A}},\enspace \overline{\mathbf{B}}u_1) = (\overline{\mathbf{A}}\mathbf{I},\enspace \overline{\mathbf{A}}0+\overline{\mathbf{B}}u_1) = (\overline{\mathbf{A}},\enspace \overline{\mathbf{B}}u_1)\)
\(s_2 = s_1 \bullet c_2 =(\overline{\mathbf{A}},\enspace \overline{\mathbf{B}}u_1) \bullet (\overline{\mathbf{A}},\enspace \overline{\mathbf{B}}u_2) = (\overline{\mathbf{A}}^2,\enspace \overline{\mathbf{A}}\overline{\mathbf{B}}u_1 + \overline{\mathbf{B}}u_2 )\)
\(s_3 = s_2 \bullet c_3 = (\overline{\mathbf{A}}^2,\enspace \overline{\mathbf{A}}\overline{\mathbf{B}}u_1 + \overline{\mathbf{B}}u_2 ) \bullet (\overline{\mathbf{A}},\enspace \overline{\mathbf{B}}u_3) = (\overline{\mathbf{A}}^3,\enspace \overline{\mathbf{A}}^2\overline{\mathbf{B}}u_1 + \overline{\mathbf{A}}\overline{\mathbf{B}}u_2 + \overline{\mathbf{B}}u_3)\)
\(s_4 = s_3 \bullet c_4 = (\overline{\mathbf{A}}^3,\enspace \overline{\mathbf{A}}^2\overline{\mathbf{B}}u_1 + \overline{\mathbf{A}}\overline{\mathbf{B}}u_2 + \overline{\mathbf{B}}u_3) \bullet (\overline{\mathbf{A}},\enspace \overline{\mathbf{B}}u_4)\\ = (\overline{\mathbf{A}}^4, \enspace \overline{\mathbf{A}}^3\overline{\mathbf{B}}u_1 + \overline{\mathbf{A}}^2\overline{\mathbf{B}}u_2 + \overline{\mathbf{A}}\overline{\mathbf{B}}u_3 + \overline{\mathbf{B}}u_4).\)
Pour obtenir les états \(x_i\), nous devrions alors prendre le deuxième élément de chaque tuple \(s_i\).
Procéder de manière séquentielle n’est pas la plus efficace puisqu’il est possible de paralléliser le calcul d’une récurrence avec le parallel scan. Ci-dessous une illustration de son fonctionnement dans le cadre de notre séquence de taille \(L\) = 4 :
 |
|---|
| Figure 20 : Fonctionnement du parallel scan dans le cadre du S5 |
A nouveau, pour obtenir les états \(x_i\), nous devrions alors prendre le deuxième élément de chaque tuple \(s_i\).
Vous remarquerez ici qu’il est possible de calculer \(s_2\) et \(i_4\) en parallèle, puis \(s_1\), \(s_3\) et \(s_4\) en parallèle. On passe alors de 4 calculs séquentiels à seulement 2. La complexité du parallel scan étant en \(O(log(L))\).
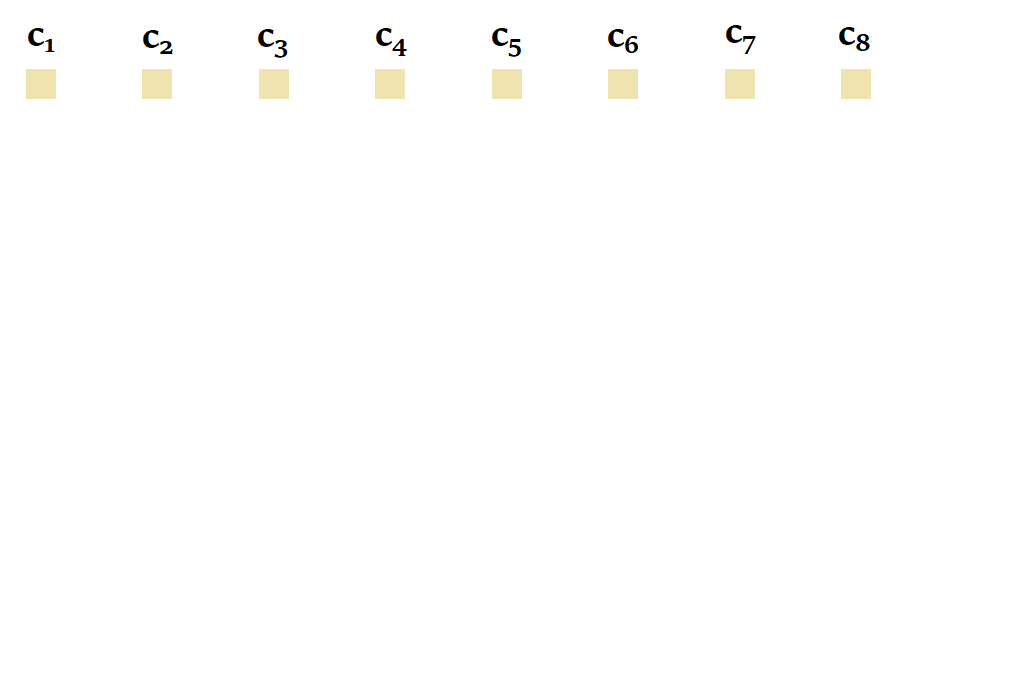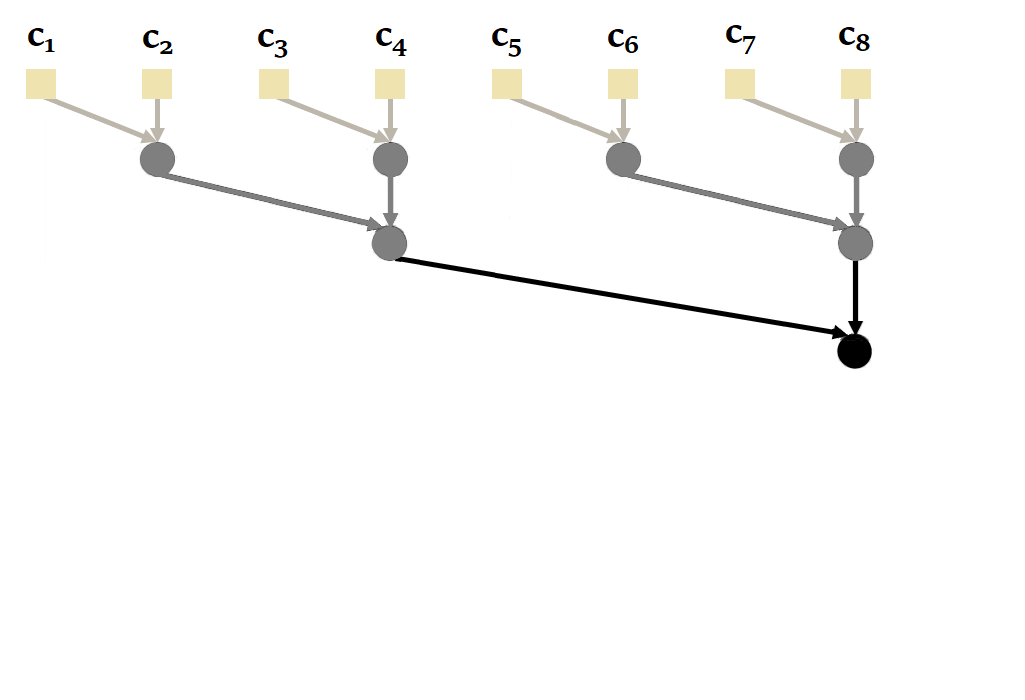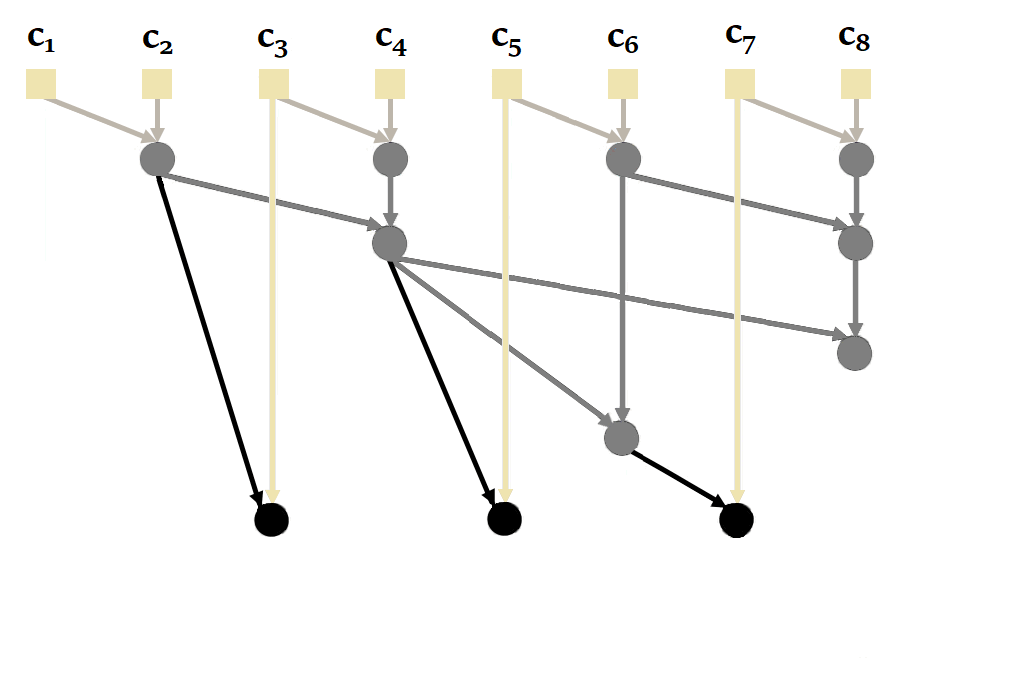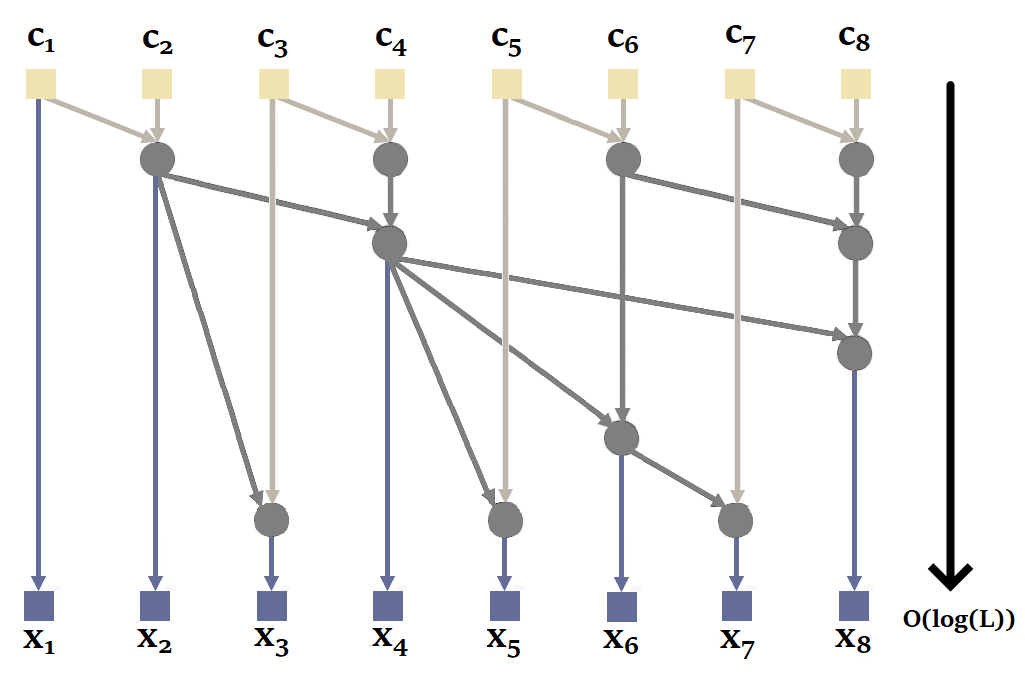 |
|---|
| Figure 21 : Fonctionnement du parallel scan d’une manière générale. Inspiré de l’animation de Scott Linderman. |
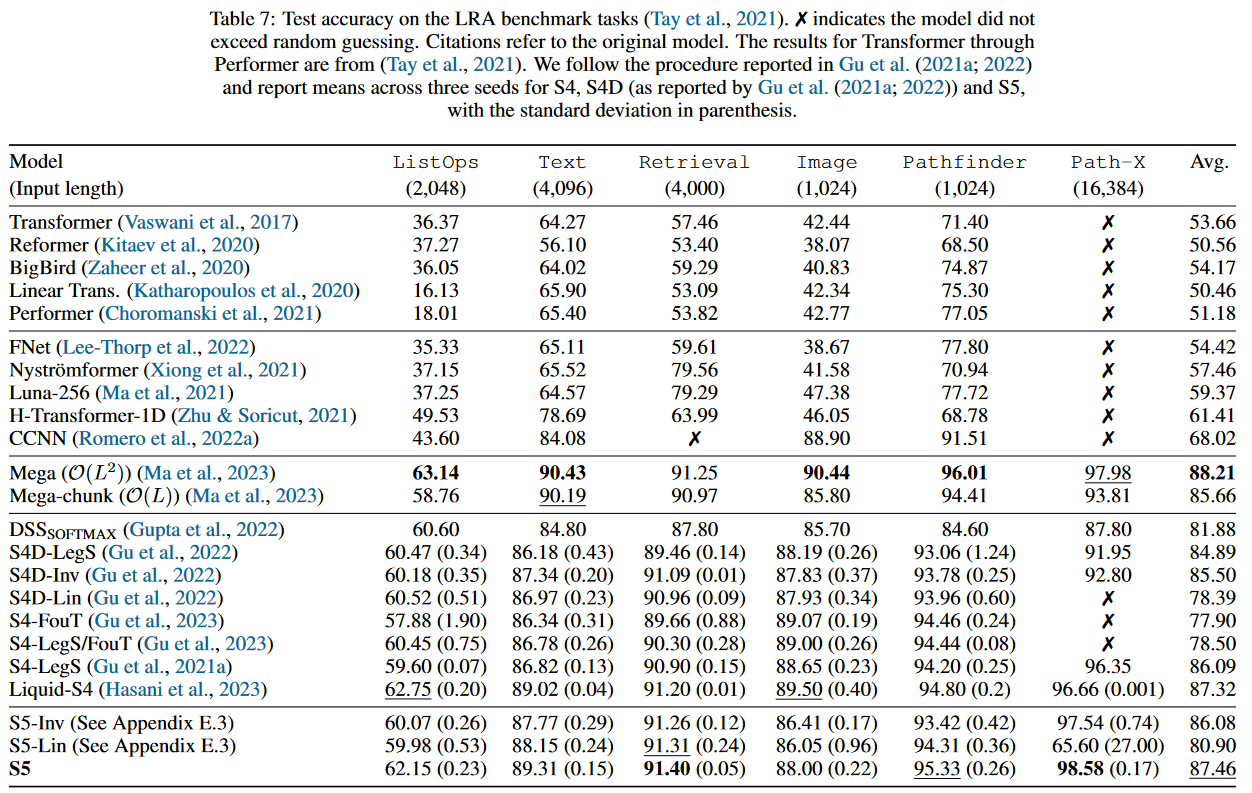
Concernant les performances du S5, celui-ci se classe deuxième sur le LRA :
 |
|---|
| Figure 22 : Les résultats du S5 sur le benchmark LRA |
Notons qu’en plus du LRA, les auteurs du S5 comparent leur modèle sur le Speech Commands, le pendulum regression dataset ainsi que sMNIST, psMNIST et sCIFAR. L’ensemble des résultats est disponible dans l’Appendix du papier qui contient également une étude d’ablation.
Pour aller plus loin
L’implémentation officielle est disponible sur GitHub.
Les échanges sur Open Review.
SGConv
Le 17 octobre 2022, What Makes Convolutional Models Great on Long Sequence Modeling? LI, CAI et al. indiquent trouver le S4 trop complexe car il nécessite un paramétrage et des schémas d’initialisation sophistiqués (= HiPPO). Et par conséquent qu’il est moins intuitif et difficile à utiliser pour les personnes ayant des connaissances préalables limitées. Ainsi leur objectif est de démystifier le S4 en se focalisant sur la vue convolutive de ce dernier.
Ils identifient deux principes critiques dont bénéficie S4 et qui sont suffisants pour constituer un modèle convolutif global performant :
1) La paramétrisation du noyau convolutif doit être efficace dans le sens où le nombre de paramètres doit augmenter de façon sous-linéaire avec la longueur de la séquence.
2) Le noyau doit avoir une structure décroissante selon laquelle les poids pour la convolution avec les voisins les plus proches sont plus importants que ceux des voisins les plus éloignés.
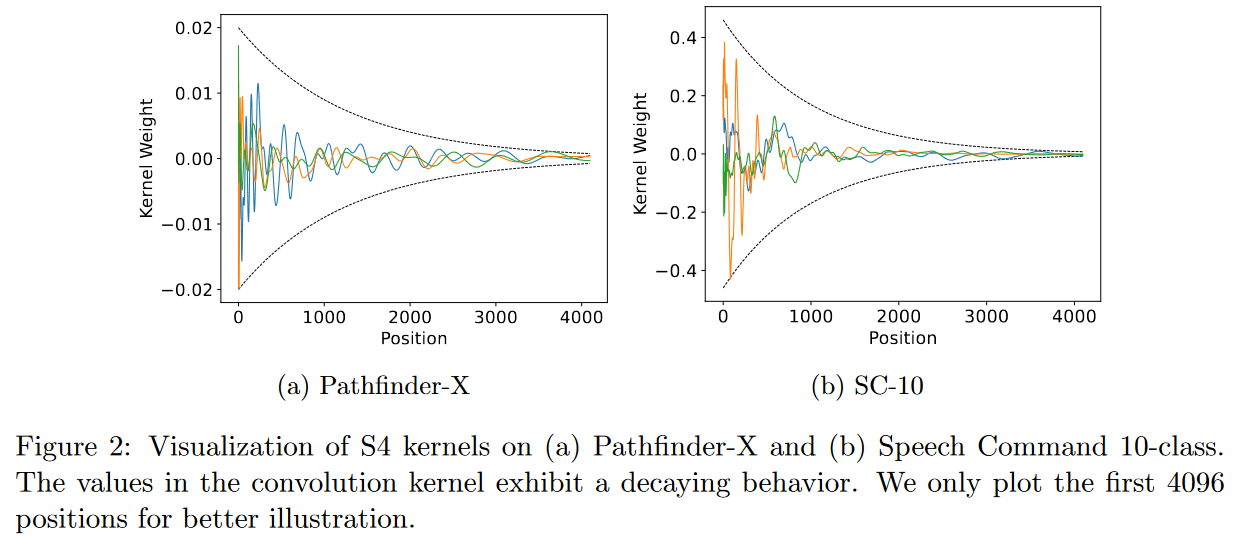 |
|---|
| Figure 23 : Respecter les deux principes critiques énoncés par les auteurs revient à avoir des noyaux de convolution ressemblant à ceux visibles sur la figure. |
Sur la base de ces deux principes, ils proposent un modèle convolutif efficace appelé Convolution globale structurée (SGConv).
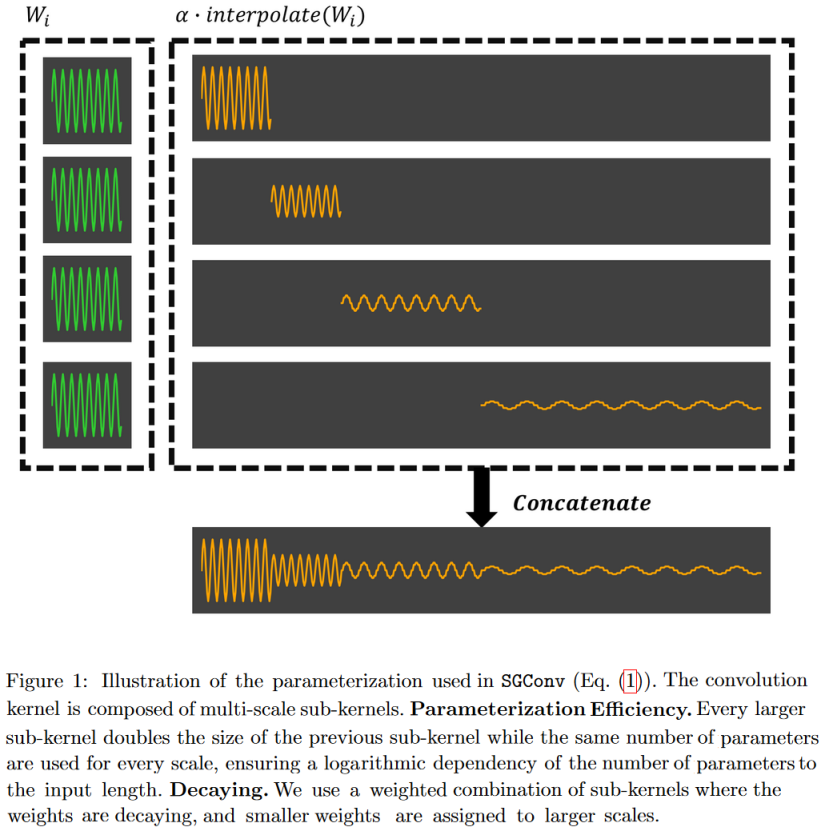 |
|---|
| Figure 24 : Le SGConv construit les noyaux de convolution comme la concaténation de sinusoïdes successivement plus longues mais de norme plus faible. L’avantage de cette forme est qu’elle permet une convolution très rapide dans le domaine des fréquences. |
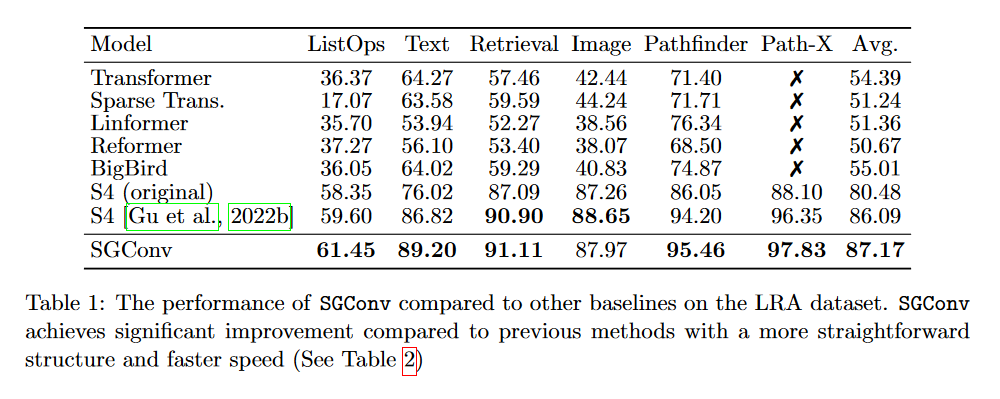
Les auteurs du SGConv indiquent qu’ils obtiennent de meilleurs résultats que le S4 sur plusieurs tâches (textes, audios, images). Nous ne les détaillerons pas toutes. Intéressons-nous seulement au LRA :
 |
|---|
| Figure 25 : Résultats du SGConv sur le LRA. |
En effet, en regardant ce tableau, on peut effectivement constater que le SGConv fait mieux que les deux versions du S4. Néanmoins, il est curieux que les auteurs n’intègrent pas le Mega, le Liquid-S4 ou encore le S5 dans leur comparaison qui pourtant obtiennent de meilleurs résultats en utilisant un noyau de convolution qui est une somme de fonctions exponentielles décroissantes.
De plus, alors que tous les modèles s’étant évaluer sur le LRA traitent les données comme des séquences 1D, le SGConv intègre implicitement un biais inductif 2D pour les tâches d’image, y compris PathX ce qui est questionnable.
Au final, le SGConv semble donc avoir des performances similaires aux variantes de SSM les plus récentes mais en perdant la vue récurrente du S4.
Ce papier apparaît néanmoins comme le premier se focalisant uniquement sur la vue convolutive d’un SSM.
Pour aller plus loin
L’implémentation officielle est disponible sur GitHub.
Les échanges sur Open Review.
Autres modèles
Deux autres papiers « théoriques » ont été publié en 2022. Le Pretraining Without Attention de WANG et al. qui présente le BiGS et le Hungry Hungry Hippos: Towards Language Modeling with State Space Models de FU, DAO et al. introduisant le H3.
Du fait de leur publication tardive (respectivement les 20 et 28 décembre 2022) et de leur communication effectuée en 2023 après les V2 de chacun de ces papiers, je traiterais ces modèles dans le prochain article de la série sur les SSM.
Applications des SSM
SaShiMi
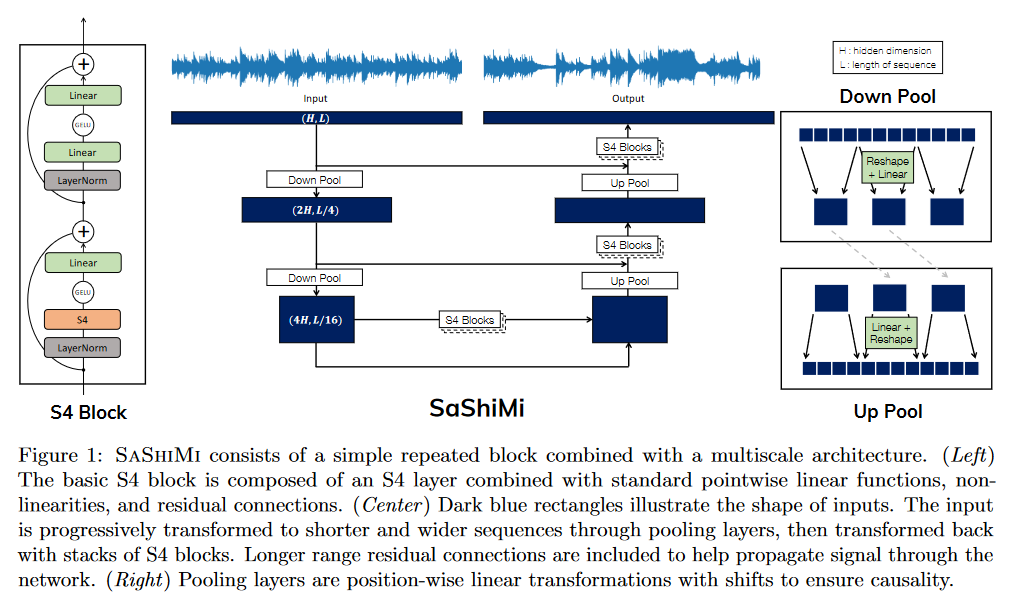
Dans It’s Raw! Audio Generation with State-Space Models paru le 20 février 2022, GOEL, GU et al. appliquent le S4 à de la génération d’audio de manière causale.
Contrairement aux méthodes reposant sur le conditionnement à partir de textes, de spectrogrammes, etc., il s’agit d’une méthode opérant directement sur le signal d’entré permettant de se comparer notamment au WaveNet de OORD et al. (2016).
SaShiMi peut s’entraîner directement sur des séquences de plus de 100K (8s audio) sur un seul GPU V100, comparé aux limitations de longueur de contexte auxquelles font face des modèles comme WaveNet. Il utilise efficacement ce long contexte pour améliorer l’estimation de la densité.
Les auteurs ont comparé leur modèle sur divers benchmarks portant notamment sur de la génération de musique de piano ou encore de la parole (énonciation de chiffres).
Il est possible de consulter les audios générés ici.
 |
|---|
| Figure 26 : Vue d’ensemble de l’architecture de Sashimi |
Pour aller plus loin
L’implémentation officielle est disponible sur GitHub.
ViS4mer
ISLAM et BERTASIUS introduisent le 4 avril 2022 le ViS4mer dans leur Long Movie Clip Classification with State-Space Video Models.
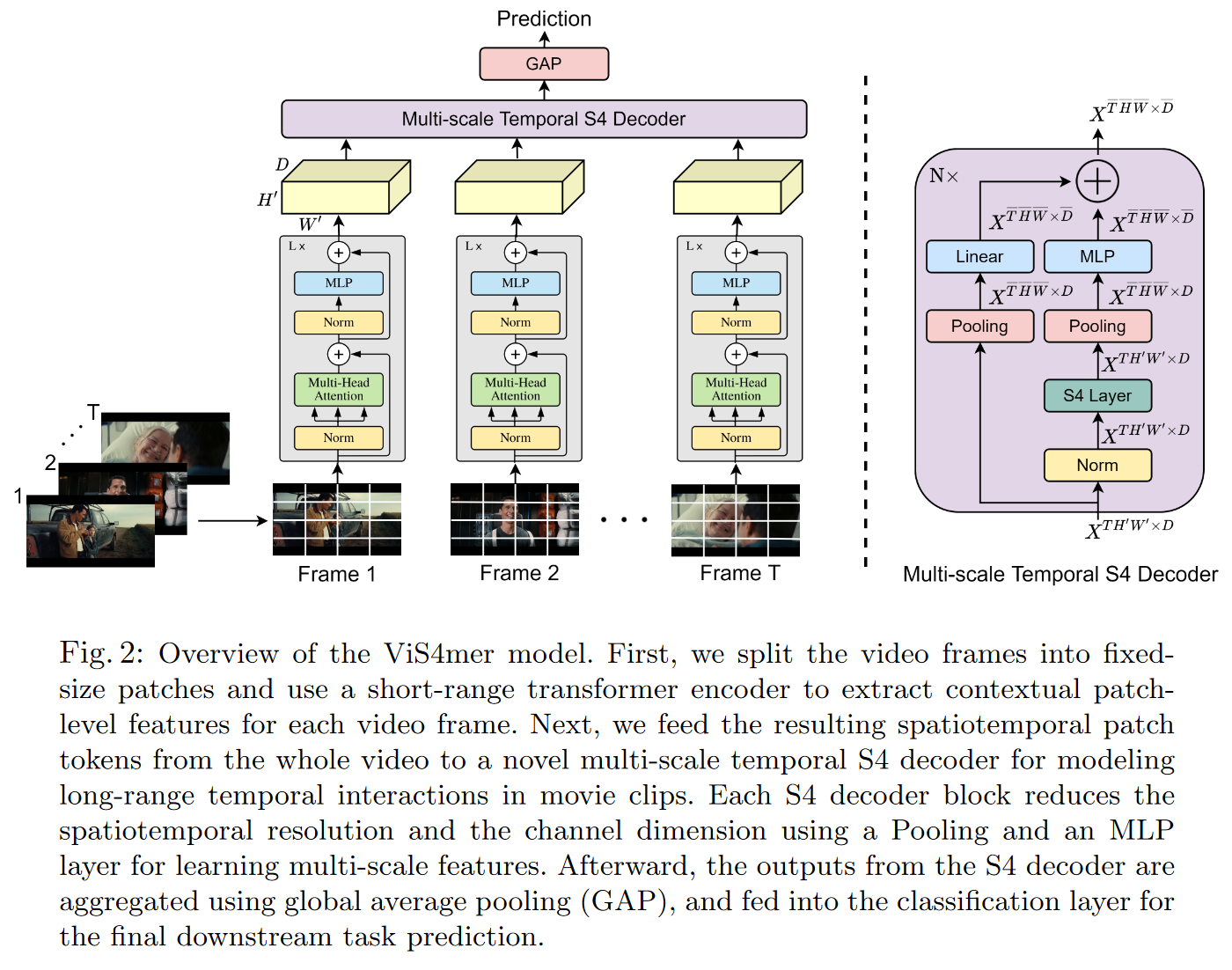
Il s’agit d’un hybride entre un S4 et un Transformer afin de réaliser de la classification de (longues) vidéos. Plus précisément, le modèle utilise un encodeur Transformer standard pour l’extraction des caractéristiques spatiotemporelles à courte distance, et un décodeur S4 temporel multi-échelle pour le raisonnement temporel à longue distance. Le modèle alors obtenu apparaît comme étant 2,6 fois plus rapide et 8 fois plus efficace en termes de mémoire qu’un Transformer.
Il s’agit à ma connaissance du premier papier à avoir mis en avant l’intérêt d’hybrider des SSM et des Transformers.
 |
|---|
| Figure 27 : Vue d’ensemble du décodeur du ViS4mer |
ViS4mer obtient des résultats de pointe dans 6 des 9 tâches de classification de vidéos de longue durée sur le benchmark Long Video Understanding (LVU) de WU et KRÄHENBÜHL (2021) qui consiste à classer des vidéos ayant une durée de 1 à 3 min. Le modèle semble également avoir de bonnes capacités de généralisation en obtenant des résultats compétitifs sur les jeux de données Breakfast et COIN procedural activity alors qu’il a vu 275 fois moins de données.
Pour aller plus loin
L’implémentation officielle est disponible sur GitHub.
CCNN
Le 7 juin 2022, ROMERO, KNIGGE et al. introduisent le CCNN dans leur papier Towards a General Purpose CNN for Long Range Dependencies in ND.
Ils partent de l’idée que les réseaux de neurones convolutifs sont puissants mais doivent être adaptés spécifiquement à chaque tâche :
• Longueur de l’entrée : 32x32, 1024x1024 → Comment modéliser les dépendances à longue distance ?
• Résolution de l’entrée : 8kHz, 16kHz → Dépendances à longue distance, agnosticité de la résolution ?
• Dimensionnalité de l’entrée : 1D, 2D, 3D → Comment définir les noyaux convolutifs ?
• Tâche : Classification, Segmentation, … → Comment définir les stratégies d’échantillonnage haut-bas ?
Est-il alors possible de concevoir une architecture unique, avec laquelle les tâches peuvent être résolues indépendamment de la dimensionnalité, de la résolution et de la longueur de l’entrée, sans modification de l’architecture ?
Oui et ceci grâce au CCNN qui utilise des noyaux de convolution continus.
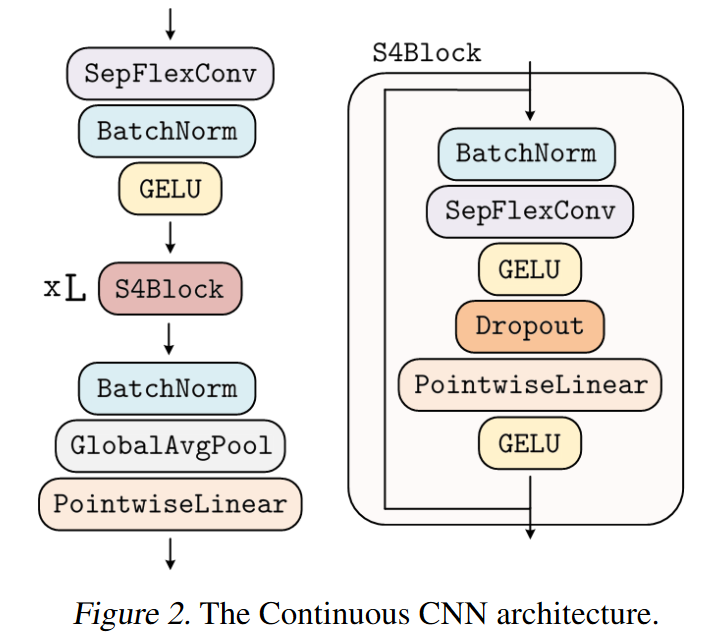
ROMERO, KNIGGE et al. s’inspirent notamment du S4 pour créer une variante de blocs résiduels efficaces qu’ils appellent bloc S4. Toutefois, contrairement au S4 qui ne fonctionne qu’avec des signaux 1D, le CCNN modélise facilement des signaux ND.
 |
|---|
| Figure 28 : Vue d’ensemble du CCNN |
Pour aller plus loin
L’implémentation officielle est disponible sur GitHub.
Les diapositives d’une présentation du papier est disponible ici
\(\mathbf{SSSD^{S4}}\)
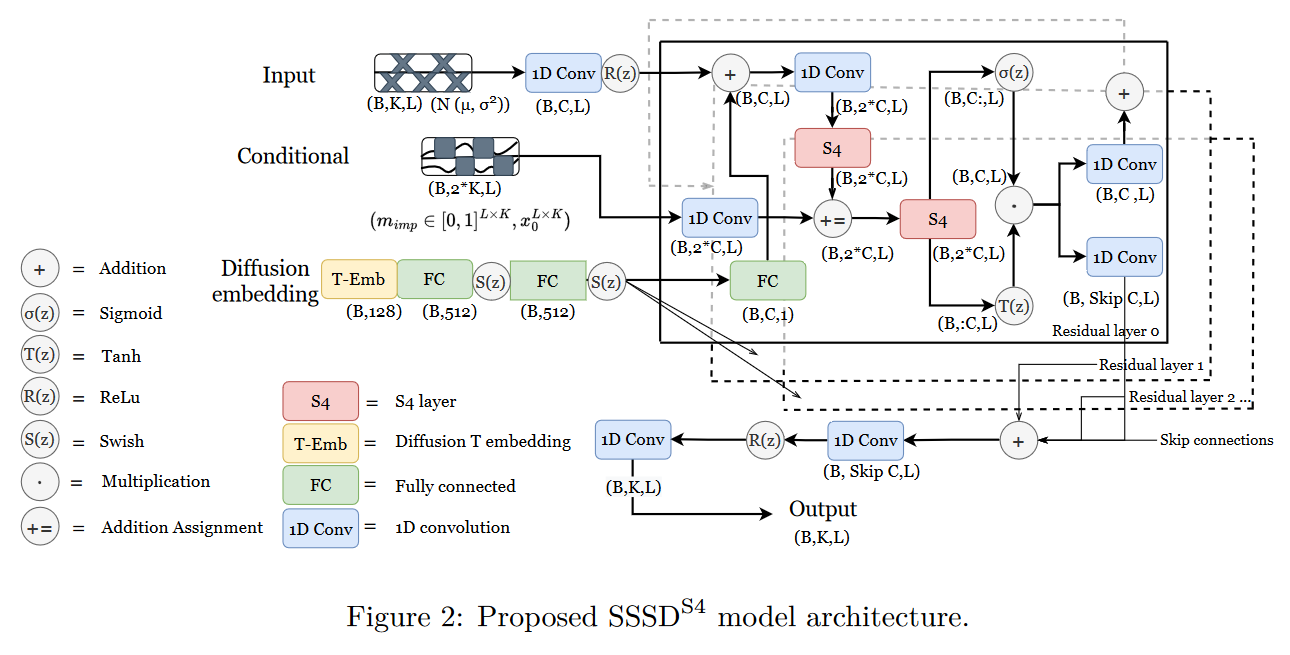
Le 19 août 2022, LOPEZ ALCARAZ et STRODTHOFF proposent dans leur papier Diffusion-based Time Series Imputation and Forecasting with Structured State Space Models un hybride entre un S4 et un modèle de diffusion pour la prédiction de données manquantes dans des séries temporelles. Leur modèle est dénommé \(\mathbf{SSSD^{S4}}\) (ou plus simplement SSSD).
 |
|---|
| Figure 29 : Vue d’ensemble du \(\mathbf{SSSD^{S4}}\) |
Pour aller plus loin
L’implémentation officielle est disponible sur GitHub.
S4ND
Le 12 octobre 2022, NGUYEN, GOEL, GU et al. présentent le S4ND: Modeling Images and Videos as Multidimensional Signals Using State Spaces.
Ce modèle étend le S4 (qui est 1D) aux signaux continus multidimensionnels tels que les images et les vidéos (là où les ConvNets et ViT apprennent sur des pixels discrets). Pour cela ils transforment l’ODE standard du S4 en une EDP multidimensionnelle :
\[\begin{aligned} x'(t) &= \mathbf{A}x(t) + \mathbf{B}u(t) \\ y(t) &= \mathbf{C}x(t) \end{aligned}\]devient :
\[\begin{aligned} \frac{\partial}{\partial t^{(1)}} x(t^{(1)}, t^{(2)}) &= (\mathbf{A}^{(1)} x^{(1)}(t^{(1)}, t^{(2)}), x^{(2)}(t^{(1)}, t^{(2)})) + \mathbf{B}^{(1)} u(t^{(1)}, t^{(2)}) \\ \frac{\partial}{\partial t^{(2)}} x(t^{(1)}, t^{(2)}) &= (x^{(1)}(t^{(1)}, t^{(2)}), \mathbf{A}^{(2)} x^{(2)}(t^{(1)}, t^{(2)})) + \mathbf{B}^{(2)} u(t^{(1)}, t^{(2)}) \\ y(t^{(1)}, t^{(2)}) &= \langle \mathbf{C}, x(t^{(1)}, t^{(2)}) \rangle \end{aligned}\]avec \(\mathbf{A}^{(\tau)} \in \mathbb{C}^{N^{(\tau)} \times N^{(\tau)}} \), \( \mathbf{B}^{(\tau)} \in \mathbb{C}^{N^{(\tau)} \times 1} \), \( \mathbf{C} \in \mathbb{C}^{N^{(1)} \times N^{(2)}}\), avec comme condition initiale de l’EDP linéaire \(x(0, 0) = 0\).
En fonction du jeu de données testé, les auteurs obtiennent des résultats similaires ou plus performants que ceux d’un ViT ou un ConvNext.
L’intérêt principal du S4ND étant qu’il peut fonctionner avec différentes résolutions via différents taux d’échantillonnage. Les auteurs mettent en avant cette caractéristique à travers deux expériences :
1) En zéro-shot, S4ND surpasse un Conv2D de plus de 40 points lorsqu’il est entraîné sur des images \(8\times8\) et testé sur des images \(32\times32\).
2) Avec un redimensionnement progressif, S4ND peut accélérer l’entraînement de 22% avec une baisse de la précision finale de ∼1% par rapport à l’entraînement à la seule haute résolution.
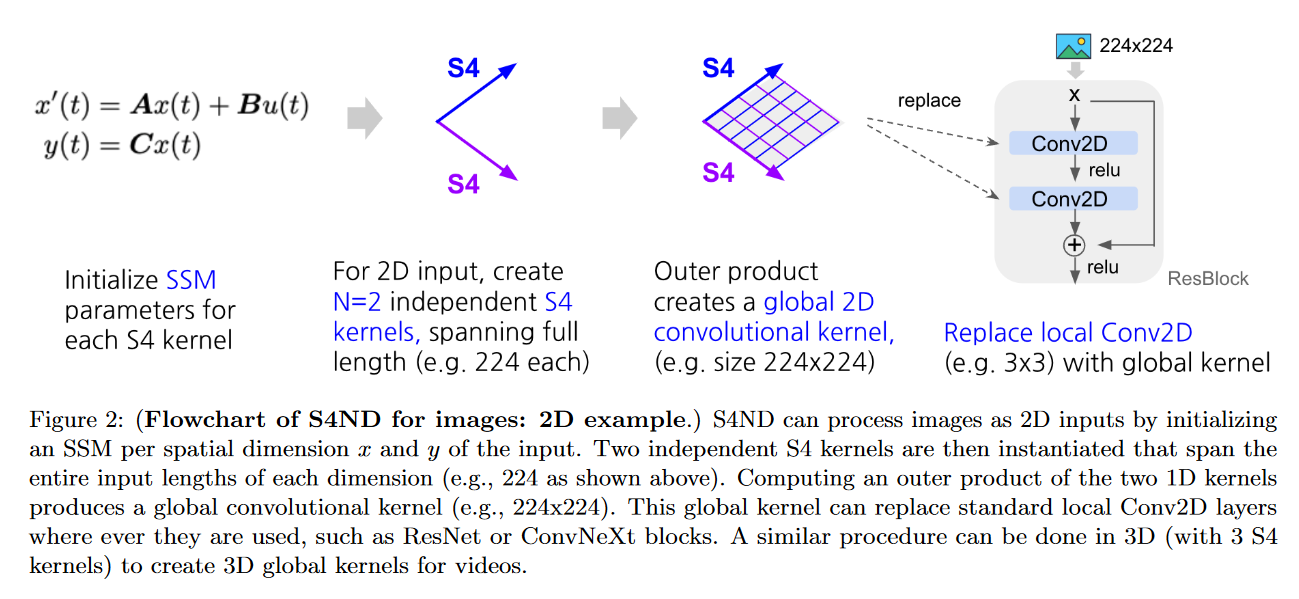 |
|---|
| Figure 30 : Exemple du S4ND pour des images 2D |
Pour aller plus loin
L’implémentation officielle est disponible sur GitHub.
Une information complètement inutile mais amusante : les auteurs ont appelé leur fichier TeX Darude S4NDstorm.
Conclusion
Nous avons donc fait une revue des différents modèles de SSM parus en 2022.
Il s’agit d’une année où les travaux se sont principalement portés sur une amélioration/simplification du S4 via diverses approches (diagonalisation, gating, LTC, etc.). Lors de cette année 2022, nous avons également pu voir les premières applications des SSM.
Avec le SGConv et le S5, nous pouvons aussi apercevoir les prémices d’un phénomène qui, comme nous le verrons dans l’article suivant, s’accentuera en 2023. A savoir l’émergence de travaux se focalisant uniquement sur la vue convolutive des SSM (par exemple le Hyena et ses dérivés) ou se focalisant uniquement sur la vue récurrente des SSM (par exemple le Mamba).
Références
- Combining Recurrent, Convolutional, and Continuous-time Models with Linear State-Space Layers d’Albert GU, Isys JOHNSON, Karan GOEL, Khaled SAAB, Tri DAO, Atri RUDRA, Christopher RÉ (2021)
- Efficiently Modeling Long Sequences with Structured State Spaces d’Albert GU, Karan GOEL, et Christopher RÉ (2021)
- HiPPO: Recurrent Memory with Optimal Polynomial Projections d’Albert GU, Tri DAO, Stefano ERMON, Atri RUDRA, Christopher RÉ (2020)
- How to Train Your HiPPO d’Albert GU, Isys JOHNSON, Aman TIMALSINA, Atri RUDRA, and Christopher RÉ (2022)
- Long Range Arena: A Benchmark for Efficient Transformers de Yi TAY, Mostafa DEHGHANI, Samira ABNAR, Yikang SHEN, Dara BAHRI, Philip PHAM, Jinfeng RAO, Liu YANG, Sebastian RUDER et Donald METZLER (2020)
- Diagonal State Spaces are as Effective as Structured State Spaces de Ankit GUPTA, Albert GU et Jonathan BERANT (2022)
- Speech Commands: A Dataset for Limited-Vocabulary Speech Recognition de Pete WARDEN (2018)
- Simplifying and Understanding State Space Models with Diagonal Linear RNNs de Ankit GUPTA, Harsh MEHTA et Jonathan BERANT (2022)
- On the Parameterization and Initialization of Diagonal State Space Models d’Albert GU, Ankit GUPTA, Karan GOEL, Christopher RÉ
- Long Range Language Modeling via Gated State Spaces d’Harsh MEHTA, Ankit GUPTA, Ashok CUTKOSKY et Behnam NEYSHABUR (2022)
- Language Modeling with Gated Convolutional Networks de Yann N. DAUPHIN, Angela FAN, Michael AULI et David GRANGIER (2016)
- GLU Variants Improve Transformer de Noam SHAZEER (2020)
- Transformer Quality in Linear Time de Weizhe HUA, Zihang DAI, Hanxiao LIU et Quoc V. LE (2022)
- Mega: Moving Average Equipped Gated Attention de Xuezhe MA, Chunting ZHOU, Xiang KONG, Junxian HE, Liangke GUI, Graham NEUBIG, Jonathan MAY et Luke ZETTLEMOYER (2022)
- Liquid Structural State-Space Models de Ramin HASANI, Mathias LECHNER, Tsun-Hsuan WANG, Makram CHACHINE, Alexander AMINI et Daniela RUS (2022)
- Liquid Time-constant Networks de Ramin HASANI, Mathias LECHNER, Alexander AMINI, Daniela RUS et Radu GROSU (2021)
- Simplified State Space Layers for Sequence Modeling de Jimmy T.H. SMITH, Andrew WARRINGTON et Scott W. LINDERMAN (2022)
- Toward a Robust Estimation of Respiratory Rate From Pulse Oximeters de Marco A. F. PIMENTEL, Alistair E. W. JOHNSON, Peter H. CHARLTON, Drew BIRRENKOTT, Peter J. WATKINSON, Lionel TARASSENKO et David A. CLIFTON (2017)
- What Makes Convolutional Models Great on Long Sequence Modeling? de Yuhong LI, Tianle CAI, Yi ZHANG, Deming CHEN et Debadeepta DEY (2022)
- Pretraining Without Attention de Junxiong WANG, Jing Nathan YAN, Albert GU et Alexander M. RUSH (2022)
- Hungry Hungry Hippos: Towards Language Modeling with State Space Models de Daniel Y. FU, Tri DAO, Khaled K. SAAB, Armin W. THOMAS, Atri RUDRA et Christopher RÉ (2022)
- It’s Raw! Audio Generation with State-Space Models de Karan GOEL, Albert GU, Chris DONAHUE, Christopher RÉ (2022)
- WaveNet: A Generative Model for Raw Audio de Aaron van den OORD, Sander DIELEMAN, Heiga ZEN, Karen SIMONYAN, Oriol VINYALS, Alex GRAVES, Nal KALCHBRENNER, Andrew SENIOR et Koray KAVUKCCUOGLU
- Long Movie Clip Classification with State-Space Video Models de Md Mohaiminul ISLAM, Gedas BERTASIUS (2022)
- Long Video Understanding de Chao-Yuan WU et Philipp KRÄHENBÜHL (2021)
- Towards a General Purpose CNN for Long Range Dependencies in ND de David W. ROMERO, David M. KNIGGE, Albert GU, Erik J. BEKKERS, Efstratios GAVVES, Jakub M. TOMCZAK, Mark HOOGENDOORN (2022)
- Diffusion-based Time Series Imputation and Forecasting with Structured State Space Models de Juan Miguel LOPEZ ALCARAZ, Nils STRODTHOFF (2022)
- S4ND: Modeling Images and Videos as Multidimensional Signals Using State Spaces de Eric NGUYEN, Karan GOEL, Albert GU, Gordon W. DOWNS, Preey SHAH, Tri DAO, Stephen A. BACCUS, Christopher RÉ (2022)
Citation
@inproceedings{ssm_in_2022_blog_post,
author = {Loïck BOURDOIS},
title = {Évolution des State Space Models (SSM) en 2022},
year = {2023},
url = {https://lbourdois.github.io/blog/ssm/ssm_en_2022}
}